Induced drag

The wing induced drag coefficient taking into account of compressibility is equal

, (5.9)

Where 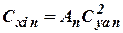- induced drag of the “deformed” wing in incompressible gas flow; 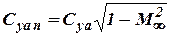; the polar pull-off factor is equal to:

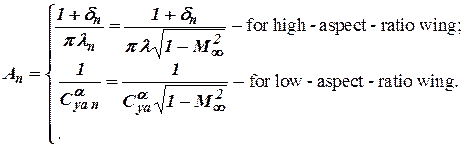
After substitution 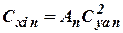, 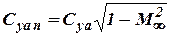and into (5.9) we again receive

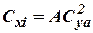, (5.10)

where - for high-aspect-ratio wings, 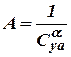- for low-aspect-ratio wings.

Thus formula of induced drag in gas subsonic flow is kept in a prior form (at angles of attack, where the linear dependence 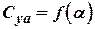. Polar does not vary too (at condition of ).

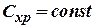5.3. Moment characteristics.
Location of center of pressure and aerodynamic center.

The factor of wing aerodynamic moment of pitch relatively to axis 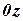passing through center of forces reductions is determined by the formula

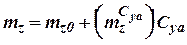, (5.11)

at that factor of pitch moment for linear part of dependence is determined as

Where 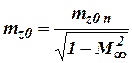- factor of pitch aerodynamic moment at 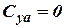, 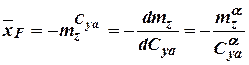- relative coordinate of aerodynamic center position.

The position of aerodynamic center 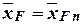and center of pressure does not depend on Mach numbers 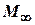for a wing in subsonic and incompressible gas flows!

Received result is approximate for low-aspect-ratio wings with taking into account the non-linear effects. (it is exact at ). For tapered high-aspect-ratio wings it is possible to offer the following formula for definition of aerodynamic center location relatively to wing top:

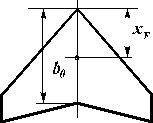Fig. 5.7.

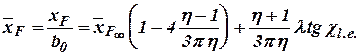
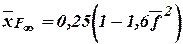- airfoil.

It is noteworthy, that if concepts of and 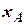are used, then position of aerodynamic center relatively to the leading edge MAC in shares of for wings of large aspect ratio is determined by the formula:

Fig. 5.8.

;

.

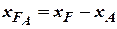It is possible to consider this ratio as fair for wings with curvilinear edges or with fracture (Fig. 5.8). At that position of aerodynamic center relatively to wing top is determined by the formula:

.

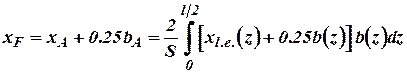There is no the common formula for low-aspect-ratio wings. In particular cases: 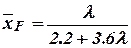- rectangular wing, 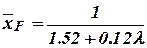- triangular wing.

It is noteworthy, that the aerodynamic center displaces forward with decreasing of 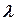for rectangular wing (at 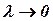, and all aerodynamic load is concentrated on the leading edge), and the aerodynamic center with 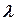reduction displaces back for triangular wing (at 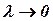, , 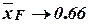more precisely ).

5.4. Wing critical Mach number .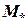

Fig. 5.9. Christianovich dependence

The critical Mach number 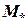determines the upper border of subsonic flows and the above mentioned formulae are fair at condition of 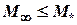. Generally 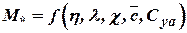. Parameters 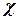, and have the greatest influence. The value 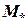can be defined by theoretical curve by
S.A. Christianovich (Fig. 5.9), having the diagram of distribution of pressure factors 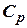along wing surface in incompressible flow. It is also possible to use the following formula for assessment 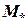of wings with ordinary airfoils (Fig. 5.10) at lift coefficient value :

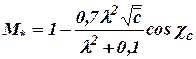, (5.12)

Where 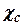- sweep angle at a line of maximum thickness.

Other formula

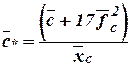; , (5.13)

Where 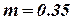- classical airfoil, - supercritical airfoil.

As it is visible from the above mentioned formulae, the value of 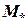depends on relative thickness and airfoil camber , on the airfoil shape (first of all on maximum thickness location 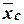) and on the wing plan form , .

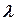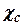It is possible to increase 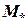by application of supercritical airfoils (Fig. 5.11). They are characterized by more uniform distribution of a pressure factor chord lengthwise.

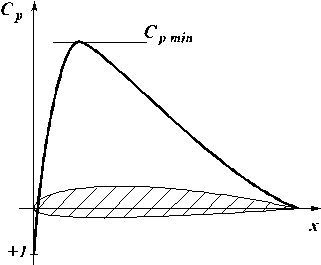
Fig. 5.10. Pressure distribution on the upper surface for ordinary airfoil

Fig. 5.11. Pressure distribution on the upper surface for supercritical airfoil

The account of 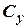influence can be done by the following formula

. (5.14)

It is possible to use dependence for supercritical airfoil and wings with such airfoils:

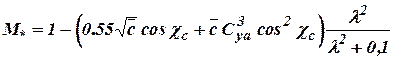. (5.15)

At the last formula gives for supercritical airfoils .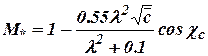

Дата добавления: 2014-12-16