Wings of small aspect ratio

It is necessary to take into account the non-linear effects which occur at flow about wings of small aspect ratio in dependence of a lift coefficient on an angle of attack 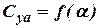(Fig. 4.6)

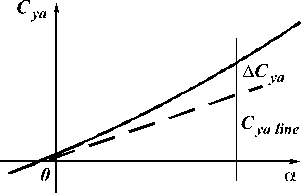Fig. 4.6.

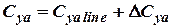
where .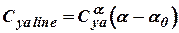

It is also possible to define values of 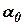and 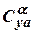by the formulae for large aspect ratio wings at The value of derivative can be determined by the formula for a wing of extremely small aspect ratio 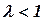, and the angle of zero lift for the wing with unswept trailing edge is equal to an angle of the trailing edge deflection , where - equation of a surface of a wing, 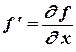, - trailing edge coordinates.

The non-linear additive can be calculated by the formula which is fair at any Mach numbers (the linear theory of subsonic flow concerns only to a linear part of the dependence).

(4.7)

At a supersonic leading edge (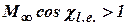) the non-linear additive disappears and .

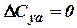With decreasing of 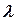the derivative 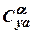decreases, and the non-linear additive 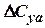grows (Fig. 4.7, 4.8).

Fig. 4.7. Character of changing of the non-linear additive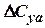

Fig. 4.8. Character of changing of the non-linear additive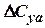

Дата добавления: 2014-12-16