
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Некоторые законы распределения случайных величин
|
|
|
|
1. Биномиальное распределение. Пусть производится п испытаний, причем вероятность появления события А в каждом испытании равна р и не зависит от исхода других испытаний (независимые испытания). Так как вероятность наступления события А в одном испытании равна р, то вероятность его ненаступления равна q = 1 - р.
Найдем вероятность того, что при п испытаниях событие А наступит т раз (m £ п).
Пусть событие А наступило в первых т испытаниях т раз и не наступило во всех последующих испытаниях. Это сложное событие можно записать в виде произведения: 
Общее число сложных событий, в которых событие А наступает т раз, равно числу сочетаний из п элементов по т элементов. При этом вероятность каждого сложного события равна: ртqn-т. Так как эти сложные события являются несовместимыми, то вероятность их суммы равна сумме их вероятностей. Итак, если Рп(т) есть вероятность появления события А т раз в п испытаниях, то
Рп(т) = 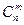 ртqn-т
ртqn-т
или
Рп(т) =  ртqn-т. (9.15)
ртqn-т. (9.15)
Формулу (9.15) называют формулой Бернулли.
Пример 9.12. Пусть всхожесть семян данного растения составляет 90%. Найдем вероятность того, что из четырех посеянных семян взойдут: а) три; б) не менее трех.
Решение, а) В данном случае п = 4, т = 3, p = 0,9, q= 1 -р = 0,1. Применим формулу Бернулли (9.15):
Р4(3) =  ×(0,9)3×0,1 =0,2916.
×(0,9)3×0,1 =0,2916.
б) Искомое событие А состоит в том, что из четырех семян взойдут или три, или четыре. По теореме сложения вероятностей Р(А) = Р 4(3) + Р 4(4). Но Р 4(4) = (0,9)4= 0,6561. Поэтому Р(А) = 0,2916 + 0,6561 = 0,9477.
Снова рассмотрим n независимых испытаний, в каждом из которых наступает событие А с вероятностью р. Обозначим через X случайную величину, равную числу появлений события А в п испытаниях.
Понятно, что событие А может вообще не наступить, наступить один раз, два раза и т.д. и, наконец, наступить п раз. Следовательно, возможными значениями величины А будут числа 0, 1, 2,..., п - 1, п. По формуле Бернулли можно найти вероятности этих значений:
Рп( 0 ) = qn
Рп( 1 ) =  р qn -1
р qn -1
……
Рп(т) = 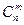 ртqn-т.
ртqn-т.
Запишем полученные данные в виде таблицы распределения:
| X | ... | т | ... | n | ||
| р | qn |  р qn -1 р qn -1
| … | 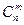 рт qn -m рт qn -m
| ... | рn |
Построенный закон распределения дискретной случайной величины X называют законом биномиального распределения.
Найдем М(Х). Очевидно, что Х i — число появлений события А в каждом испытании — представляет собой случайную величину со следующим распределением:
| X i | ||
| р i | q | р |
Поэтому М(X i ) = 0× q+ 1× р = р. Но так как X = Х 1 +... +Х n, то М(X) =np.
Найдем далее D(Х) и s(Х). Так как величина X i2 имеет распределение
| X i2 | 02 | 12 |
| р i |
то М(X i2 ) = 02× q+ 12× р = р. Поэтому D(X i ) = М(X i2 ) - М 2 (X i ) = р - p 2 = р (1- p)= pq.
Наконец, в силу независимости величин Х 1, Х2,..., Хn,
D(X) = D(X 1 ) + D(X 2 ) + ... + D(X n ) = npq.
Отсюда s(Х) = 
Пример 9.13. Случайная величина X определена как число выпавших гербов в результате 100 бросаний монеты. Вычислим математическое ожидание, дисперсию и среднее квадратическое отклонение X.
Решение. Вероятность появления герба при каждом бросании монеты р= ½.Следовательно, вероятность непоявления герба q =1 - ½ = ½. Случайная величина X имеет биномиальное распределение при п = 100 и р = ½.Поэтому
М(X) =np =100×½=50; D(X) = npq =100×½×½=25; s(Х) = 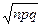 =
=  =5.
=5.
Пример 9.14. Допустим, что для хищника вероятность поимки отдельной жертвы составляет 0,4 при каждом столкновении с жертвой. Каково ожидаемое число пойманных жертв в 20 столкновениях?
Решение. Это пример биномиального распределения при n =20 и р= 0,4. Ожидаемое число есть М(Х) - пр = 20×0,4 = 8.
|
|
|
|
|
Дата добавления: 2014-11-29; Просмотров: 521; Нарушение авторских прав?; Мы поможем в написании вашей работы!