Гипергеометрическое распределение

Гипергеометрическое распределение имеет место при выборочном контроле конечной совокупности объектов объёма N по альтернативному признаку. Каждый контролируемый объект классифицируется либо как обладающий признаком A, либо как не обладающий этим признаком. Гипергеометрическое распределение имеет случайная величина Y, равная числу объектов, обладающих признаком в случайной выборке объёма , где n<N. Например, число Y дефектных единиц продукции в случайной выборке объёма из партии объёма N имеет гипергеометрическое распределение, если n<N. Другой пример — лотерея. Пусть признак A билета — это признак «быть выигрышным». Пусть всего билетов N, а некоторое лицо приобрело n из них. Тогда число выигрышных билетов у этого лица имеет гипергеометрическое распределение.

Для гипергеометрического распределения вероятность принятия случайной величиной Y значения y имеет вид

,

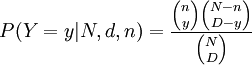где D — число объектов, обладающих признаком A, в рассматриваемой совокупности объёма N. При этом y принимает значения от до 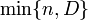, при прочих y вероятность в формуле равна нулю. Таким образом, гипергеометрическое распределение определяется тремя параметрами — объёмом генеральной совокупности N, числом объектов D в ней, обладающих рассматриваемым признаком A, и объёмом выборки .

Простой случайной выборкой объёма из совокупности объёма N называется выборка, полученная в результате случайного отбора, при котором любой из наборов из n объектов имеет одну и ту же вероятность быть отобранным. Методы случайного отбора выборок респондентов (опрашиваемых) или единиц штучной продукции рассматриваются в инструктивно-методических и нормативно-технических документах. Один из методов отбора таков: объекты отбирают один из другим, причём на каждом шаге каждый из оставшихся в совокупности объектов имеет одинаковые шансы быть отобранным. В литературе для рассматриваемого типа выборок используются также термины «случайная выборка», «случайная выборка без возвращения».

Поскольку объёмы генеральной совокупности (партии) N и выборки обычно известны, то подлежащим оцениванию параметром гипергеометрического распределения является D. В статистических методах управления качеством продукции D — обычно число дефектных единиц продукции в партии. Представляет интерес также характеристика распределения — уровень дефектности.

Для гипергеометрического распределения

, .

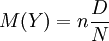Последний множитель в выражении для дисперсии близок к 1, если N> 10 n. Если при этом сделать замену 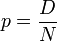, то выражения для математического ожидания и дисперсии гипергеометрического распределения перейдут в выражения для математического ожидания и дисперсии биномиального распределения. Это не случайно. Можно показать, что

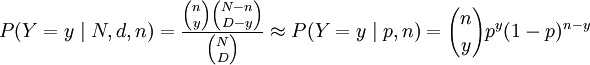, y= 0, 1, 2, …, n,

при N> 10 n, где 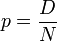. Точнее, справедливо предельное соотношение

, y= 0, 1, 2, …, n, и этим предельным соотношением можно пользоваться при N> 10 n

.

3. Распределение Пуассона. Пусть производится серия п независимых испытаний (п = 1, 2, 3,...), причем вероятность появления данного события А в этой серии Р(А)=р_n>0 зависит от ее номера п и стремится к нулю при п ®¥ (последовательность «редких событий»). Предположим, что для каждой серии среднее значение числа появлений события А постоянно, т.е. п р_n = m= const.

Отсюда р_n = m/ п.

Исходя из формулы Бернулли (9.15), для вероятности появления события А в n -й серии ровно т раз имеем выражение Р_п(т) = 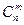р^т (1- p) ^n-т₌ .

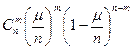Пусть т фиксировано. Тогда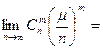

=

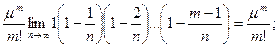
(здесь использован второй замечательный предел; см. подразд. 2.5). Поэтому

.

Если п велико, то в силу определения предела (см. подразд. 2.5) вероятность Р_п(т) сколь угодно мало отличается от . Отсюда при больших п для искомой вероятности Р_п(т) имеем приближенную формулу Пуассона (для простоты знак приближенного равенства опущен)

Р_п(т) = , где m= пр_n.

Определение. Говорят, что случайная величина X распределена по закону Пуассона, если эта величина задана таблицей:

X					….
р					….

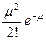
Здесь m — фиксированное положительное число (разным значениям m отвечают разные распределения Пуассона).

Найдем математическое ожидание дискретной величины X, распределенной по закону Пуассона. Согласно определению математического ожидания (см. подразд. 9.2, п. 2, примечание 2)

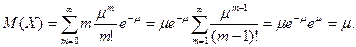
Найдем далее D(Х). Сначала найдем М(Х²):

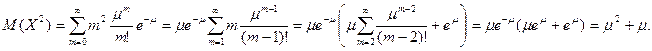Теперь по известной формуле (см. подразд. 9.3, п. 2)

D(Х)= М(Х²) - М²(Х) =

Это распределение названо в честь французского математика Симеона-Дени Пуассона (1781—1840), впервые получившего его в 1837 году.

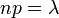Мы только что доказали, что распределение Пуассона является предельным случаем биномиального распределения, когда вероятность осуществления события мала, но число испытаний велико, причём . Точнее, справедливо предельное соотношение

 , .

Поэтому распределение Пуассона (в старой терминологии «закон распределения») часто называют также «законом редких событий».

Распределение Пуассона возникает в теории потоков событий. Доказано, что для простейшего потока с постоянной интенсивностью число событий (вызовов), происшедших за время , имеет распределение Пуассона с параметром . Следовательно, вероятность того, что за время не произойдет ни одного события, равна 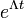, то есть функция распределения длины промежутка между событиями является экспоненциальной.

Распределение Пуассона крайне важно во многих физических и биологических задачах. Оно представляет собой грубую модель частоты встречаемости катастрофических наводнений при довольно длительном периоде наблюдений. Распределение микроэлементов в образце почвы может также приближаться к пуассоновскому.

Распределение Пуассона используется при анализе результатов выборочных потребителей товара, расчёте оперативных характеристик планов статистического приёмочного контроля в случае малых значений приёмочного уровня дефектности, для описания числа разладок статистически управляемого технологического процесса в единицу времени, числа «требований на обслуживание», поступающих в единицу времени в систему массового обслуживания, статистических закономерностей несчастных случаев и редких заболеваний, и так далее.

Описание иных параметрических семейств дискретных распределений и возможности их практического использования рассматриваются в обширной (более миллиона названий статей и книг на десятках языков) литературе по вероятностно-статистическим методам.

5. Равномерное распределение. Распределение вероятностей непрерывной случайной величины X, принимающей все свои значения из отрезка [ а; b ], называется равномерным, если ее плотность вероятности на этом отрезке постоянна, а вне его равна нулю, т. е.

Отсюда (см, подразд. 9.4, п. 1)

(9.21)

Но, как известно (см. подразд. 9.4, п. 2),

Из сравнения этого равенства с (9.21) получаем

Итак, плотность вероятности непрерывной случайной величины X, распределенной равномерно на отрезке [а; b], имеет вид

Покажем, что и

Действительно,

Далее

Пример 9.17. На отрезке [ а; b ]наугад указывают точку. Какова вероятность того, что эта точка окажется в левой половине отрезка?

Решение. Пусть X — случайная величина, равная координате выбранной точки. X распределена равномерно (в этом и состоит точный смысл слов: «наугад указывают точку»), а так как середина отрезка [ а; b ]имеет координату , то искомая вероятность равна (см. подразд. 9.4, п. 2)

Впрочем, этот результат был ясен с самого начала.

6. Закон нормального распределения. Центральная предельная теорема. Закон распределения вероятностей непрерывной случайной величины X называется нормальным, если ее дифференциальная функция f (х) определяется формулой (9.22)

где параметр а совпадает с математическим ожиданием величины X: а = М(Х), параметр s является средним квадратическим отклонением величины X: s=s(X).

В подразд. 3.8 (пример 3.47) было рассмотрено построение графика функции (кривая Гаусса). С учетом графика этой функции график функции (9.22) будет иметь вид, как на рис. 9.1. Причем его максимальная ордината равна 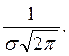Значит, эта ордината убывает с возрастанием значенияs(кривая «сжимается»к оси Ох) и возрастает с убыванием значения s (кривая «растягивается» в положительном направлении оси Оy), что отражено на рис. 9.2.

Изменение значений параметра а (при неизменном значении s) не влияет на форму кривой.

Нормальное распределение с параметрами а= 0 и s = 1 называют нормированным. Дифференциальная функция в случае такого распределения

Пусть случайная величина X распределена по нормальному закону. Тогда вероятность того, что X приметзначение, принадлежащее интервалу (а; b), согласно известной теореме (см. п. 2),

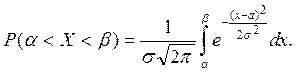
Сделаем в этом интеграле замену переменной, полагая Тогда х = =а+st, dх=s dt и

(9.23)

Используя функцию (9.19), получаем

Итак,

(9.24)

Нормальное распределение вероятностей имеет в теории вероятностей большое значение. Нормальному закону подчиняется вероятность при стрельбе по цели, в измерениях и т. п.

Дата добавления: 2014-11-29