Генеральная совокупность и выборка

Лекция 6. Элементы математической статистики

Вопросы для контроля знаний и подведения итога прочитанной лекции

1. Дайте определение случайной величины.

2.Напишите формулы для математического ожидания и дисперсии дискретной и непрерывной случайных величин.

3. Дайте определение локальной интегральной предельная теорем Лапласа

4. Напишите формулы, задающие биномиальное распределение, гипергеометрическое распределение, распределение Пуассона, равномерное распределение и нормальное распределение.

Цель: Изучить основные понятия математической статистики

План:

1. Генеральная совокупность и выборка

2. Статистическое распределение выборки. Полигон. Гистограмма.

3. Оценки параметров генеральной совокупности по ее выборке

4. Генеральная и выборочная средние. Методы их расчета.

5. Генеральная и выборочная дисперсии.

6. Вопросы для контроля знаний и подведения итога прочитанной лекции

Мы приступаем к изучению элементов математической статистики, в которой разрабатываются научно обоснованные методы сбора статистических данных и их обработки.

1. Генеральная совокупность и выборка. Пусть требуется изучить множество однородных объектов (это множество называется статистической совокупностью) относительно некоторого качественного или количественного признака, характеризующего эти объекты. Например, если имеется партия деталей, то качественным признаком может служить стандартность детали, а количественным — контролируемый размер детали.

Лучше всего произвести сплошное обследование, т.е. изучить каждый объект. Однако в большинстве случаев по разным причинам это сделать невозможно. Препятствовать сплошному обследованию может большое число объектов, недоступность их. Если, например, нужно знать среднюю глубину воронки при взрыве снаряда из опытной партии, то, производя сплошное обследование, мы уничтожим всю партию.

Если сплошное обследование невозможно, то из всей совокупности выбирают для изучения часть объектов.

Статистическая совокупность, из которой отбирают часть объектов, называется генеральной совокупностью. Множество объектов, случайно отобранных из генеральной совокупности, называют выборкой.

Число объектов генеральной совокупности и выборки называют соответственно объемом генеральной совокупности и объемом выборки.

Пример 10.1. Плоды одного дерева (200 шт.) обследуют на наличие специфического для данного сорта вкуса. Для этого отбирают 10 шт. Здесь 200 — объем генеральной совокупности, а 10 — объем выборки.

Если выборку отбирают по одному объекту, который обследуют и снова возвращают в генеральную совокупность, то выборка называется повторной. Если объекты выборки уже не возвращаются в генеральную совокупность, то выборка называется бесповторной.

На практике чаще используется бесповторная выборка. Если объем выборки составляет небольшую долю объема генеральной совокупности, то разница между повторной и бесповторной выборками незначительна.

Свойства объектов выборки должны правильно отражать свойства объектов генеральной совокупности, или, как говорят, выборка должна быть репрезентативной (представительной). Считается, что выборка репрезентативна, если все объекты генеральной совокупности имеют одинаковую вероятность попасть в выборку, т. е. выбор производится случайно. Например, для того чтобы оценить будущий урожай, можно сделать выборку из генеральной совокупности еще не созревших плодов и исследовать их характеристики (массу, качество и пр.). Если вся выборка будет сделана с одного дерева, то она не будет репрезентативной. Репрезентативная выборка должна состоять из случайно выбранных плодов со случайно выбранных деревьев.

2. Статистическое распределение выборки. Полигон. Гистограмма. Пусть из генеральной совокупности извлечена выборка, причем х ₁ наблюдалось n ₁, раз, х ₂ — п₂ раз,..., х_k — n _k раз и n ₁+ n ₂ +…+ п_k = п — объем выборки. Наблюдаемые значения x ₁, x ₂, …, x_k называют вариантами, а последовательность вариант, записанная в возрастающем порядке, — вариационным рядом. Числа наблюдений n ₁, n ₂, …, n_k называют частотами, а их отношения к объему выборки 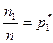, , …, — относительными частотами. Отметим, что сумма относительных частот равна единице: .

Статистическим распределением выборки называют перечень вариант и соответствующих им частот или относительных частот. Статистическое распределение можно задать также в виде последовательности интервалов и соответствующих им частот (непрерывное распределение). В качестве частоты, соответствующей интервалу, принимают сумму частот вариант, попавших в этот интервал. Для графического изображения статистического распределения используют полигоны и гистограммы.

Для построения полигона на оси Ох откладывают значения вариант х _i, на оси Оу — значения частот п _i(относительных частот ).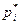

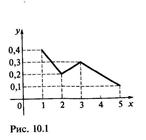
Пример 10.2. На рис. 10.1 показан полигон следующего распределения

Варианта хi
Относительная частота	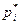0,4	0,2	0,3	0,1

Полигоном обычно пользуются в случае небольшого числа вариант. В случае большого числа вариант и в случае непрерывного распределения признака чаще строят гистограммы. Для этого интервал, в котором заключены все наблюдаемые значения признака, разбивают на несколько частичных интервалов длиной h и находят для каждого частичного интервала п_i, — сумму частот вариант, попавших в i -интервал. Затем на этих интервалах, как на основаниях, строят прямоугольники с высотами (или , где п — объем выборки).

Площадь i частичного прямоугольника равна 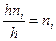, (или ).

Следовательно, площадь гистограммы равна сумме всех частот (или относительных частот), т.е. объему выборки (или единице).

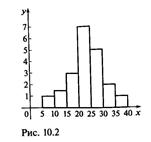
Пример 10.3. На рис. 10.2 показана гистограмма непрерывного распределения объема n = 100, приведенного в следующей таблице:

Частичный интервал h	Сумма частот вариант частичного интервала пi
5-10		0,8
10-15		1,2
15-20		3,2
20-25		7,2
25-30		4,8
30-35		2,0
35-40		0,8

Дата добавления: 2014-11-29