Сети. Сетевые модели представления информации

Способы задания графа. Изоморфные графы

В математике значительно сильнее, чем в других дисциплинах, обнаруживается черта организованности, стремление находить скрытый порядок во всем, что нас окружает...

А. Сухотин

Существуют различные способы задания графа: геометрический (рисунки, схемы, диаграммы), простое перечисление вершин и ребер, табличный. Человеку удобно работать с графом-рисунком, так как он может легко установить связь между вершинами в наглядном виде с помощью ребер, изображаемых непрерывными линиями. Такое геометрическое представление плоского графа называется его реализацией. Для машинной обработки удобнее задать граф в алгебраической форме — перечислением (списком) вершин или ребер.

Например, орграф на рис. 2.3 можно задать с помощью пар (V ₁, V ₂ ), (V ₂, V ₃ ), (V ₂, V ₃ ) и (V ₁, V ₁), что соответствует дугам (r, и, t, s). При переходе от алгебраического способа к геометрическому одному и тому же графу могут соответствовать различные изображения — изоморфные графы, при этом от правильного изображения зависит, например, свойство плоской реализуемости. Для этого нужно правильно задать сам граф.

Основным способом задания графа является перечисление всех его вершин и ребер. Но такое представление, во-первых, несимметрично (с ним трудно работать, особенно ЭВМ), во-вторых, для указания каждого ребра нужно еще раз выписывать соответствующие вершины, что плохо с точки зрения сжатия и хранения информации. Иногда граф задается таблицей, состоящей из п строк (вершины) и т столбцов (ребра). Главным во всех способах задания графа (диаграммой, матрицей, таблицей) является указание соответствия между множествами п вершин V_i и т ребер X _i.

Одним из самых распространенных способов задания графа является матричный способ. Пусть дан граф G(V, X), где V={V ₁, V ₂,..., V_п} — вершины, а Х= {Х ₁, Х₂,..., Х_т} — ребра графа.

Назовем матрицей инцидентности таблицу В, состоящую из п строк (вершины) и т столбцов (ребра), в которой:

для неориентированного графа:

b_ij = 1, если вершина V _iинцидентна ребру X_j;

b_ij = 0, если вершина V _iне инцидентна ребру X_j;

для ориентированного графа:

b_ij = 1, если вершина V _iявляется началом дуги X_j,

b_ij =0, если вершина V _iне инцидентна дуге X_j,

b_ij = -1, если вершина V _iявляется концом дуги X_j.

Очевидно, что в каждом столбце матрицы инцидентности должно быть только два ненулевых числа, так как ребро инцидентно двум вершинам. Число ненулевых элементов каждой строки — степень соответствующей вершины. Но в математике удобнее работать с квадратными матрицами, так как для них хорошо разработан соответствующий алгебраический аппарат.

Назовем матрицей смежности графа G(V, X) без кратных ребер квадратную матрицу А порядка я, в которой:

a_ij = 1, если (V_i,, V_j) Î X;

a_ij =0, если (V_i,, V_j} Ï X.

Поскольку для неориентированного графа ребра (V_i,, V_j) и (V_j,, V_i) одновременно принадлежат или не принадлежат графу, так как символизируют одно и то же ребро, то a_ij == a_ji. Матрица смежности неориентированного графа является симметрической и не меняется при транспонировании.

Хотя формально каждая вершина всегда смежна сама с собой, в матрице смежности мы будем ставить a_ij = 0, если у нее нет петли, и a_ij =1, если есть одна петля. Итак, если граф имеет матрицу смежности и не имеет петель, на главной диагонали у него всегда стоят нули.

Например, орграф на рис. 2.3 можно задать такой таблицей инцидентности (табл. 2.1).

Таблица 2.1. Таблица инцидентности орграфа

Vi	Xj
s	t	r	u
V 1	-1
V 2			-1
V 3		-1		-1

Его же можно задать матрицей B=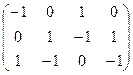

Поскольку ребра изначально не упорядочены, то, например, записывая сначала инцидентность ребра t (1-й столбец), потом ребра s (2-й столбец), получим матрицу с переставленными столбцами 1 и 2. Тогда при решении обратной задачи -восстановлении графа по его матрице инцидентности — можно получить граф лишь с точностью до изоморфизма. Поэтому в графах важно лишь отношение между вершинами (т. е. смежность), а их название и порядок не столь важны.

Граф, изображенный на рис. 2.18, задается таблицей инцидентности (табл. 2.2).

Таблица 2.2. Таблица инцидентности графа

	Xj
Х1	Х2	Х3	Х4	Х5	Х6	Х7	Х8	Х9	Х 10
V 1
V 2
V 3
V 4
V 5
V 6

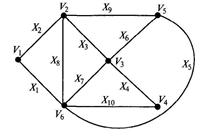
Рис. 2.18. Графическая интерпретация графа G, заданного табл. 2.2

Матрица инцидентности для него имеет вид

Этому же рисунку соответствуют таблица и матрица смежности (табл. 2.3).

Таблица 2.3. Таблица смежности графа G

Vi	V j
V 1	V2	V3	V4,	V5	V6
V 1
V 2
V 3
V 4
V 5
V 6

Граф с кратными ребрами (особенно орграф) сложно задать с помощью матрицы смежности. Сделаем это формально. Если граф неориентированный, то справедливо a_ij == a_ji. и равно кратности ребра (V_i, V_j). В частности, если i=j, то a_ij — число петель при V_i. Недостаток подобного подхода заключается в том, что остается неучтенным взаимное расположение кратных ребер. Так, ребра могут переплетаться между собой, что, к сожалению, не отразится на матрице смежности.

Заметим, что для ориентированного графа данное определение графа без кратных ребер является частным случаем графа с кратными ребрами при кратности любого ребра, равной 1 или 0. Очевидно, что для двух вершин V_i и V_j (i¹j) существуют две принципиальные возможности:

если все ребра выходят из одной и входят в другую вершину

или если для каждой вершины существуют как входящие, так и исходящие ребра.

Пусть полная кратность ребра равна n, при этом из вершины V_i в вершину V_j исходят т £ п ребер, а из V_j в V_i исходят п - т ребер. Тогда в клетке a_ij напишем m, а в клетке a_ji напишем п - т. Если есть кратные петли, то все они связаны с одной вершиной V_i. Поэтому в клетке a_ii напишем кратность петли при V_i.

Такому заданию графа присущи те же недостатки, что и неориентированному, и еще неучет взаимного расположения направлений. Однако главным недостатком служит то, что при таком определении матрицы смежности (как графа с кратными ребрами, так и без них) не всегда возможно определить по матрице смежности ориентированный граф или нет.

В матрицах инцидентности такой проблемы нет, так как наличие элемента вида -1 является критерием ориентированности графа. Для матрицы смежности несимметричность может являться достаточным условием ориентированности, но не критерием. Например, графу с матрицей смежности 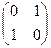может соответствовать отрезок V₁ V₂ (и две вершины) — неориентированный граф или кольцо с двумя ребрами V = {(V ₁, V ₂); (V ₂, V ₁) } — орграф. Это -существенный недостаток, и возник он как раз при попытке определения матрицы смежности для графа с кратными ребрами Поэтому для задания ориентированного графа с помощью матрицы смежности (если она получается симметричной) надо или указывать это отдельно, например А _ор , или у любого элемента матрицы написать «-».

Задача 19. Пусть граф G задан матрицей смежности А. Построить диаграмму этого графа, если

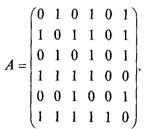Решение. Поскольку матрица А несимметрична (например a ₃₅ ¹a ₅₃) и указания на ориентированность нет, А не может яляться матрицей смежности реального графа.

Задача 20. Пусть граф G задан матрицей смежности А. Построить диаграмму этого графа, если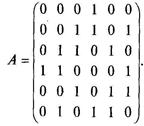

Решение. Диаграмму графа, имеющего шесть вершин, представим на рис. 2.19.

Любой ориентированный граф является бинарным отношением А под V, где V— множество вершин графа, а пары из X— ребра.

Для конечного числа V вершин отношение X можно представить тремя способами:

графически, т.е. диаграммой (рис. 2.19);

с помощью таблиц, в которых представлены 1 и 0;

с помощью матриц (в случае матриц смежности).

Такая форма записи отношений удобна при решении многих логических и производственных задач. Она также используется при машинной обработке для систематизации информации

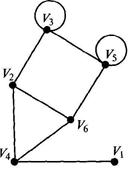
Рис. 2.19. Граф к задаче

В этом проглядывается талант исследователя охватить значительные районы явлений с помощью немногочисленных допущений, представить разносторонние совокупности предметов и процессов в сжатой, компактной форме.

А. Сухотин

Граф называется взвешенным или сетью, если каждому его ребру поставлено в соответствие некоторое число (вес). Взвешенными графами могут быть схемы в электронике, электрические схемы, карты автомобильных и железных дорог и др. Например, на картах автодорог вершины являются населенными пунктами, ребра — дорогами, а весом — числа, равные расстоянию между населенными пунктами.

В строительстве сетевые графы применяются для наглядного изображения некоторого комплекса работ или производственных процессов. Ребрам графа могут соответствовать числа, означающие длину, уклон, запланированное время и другие характеристики.

Например, последовательность работ для монтажа каркаса здания изображена в виде графа (рис. 2.20).

Числами обозначены технологические операции:

1 — рытье котлована;

2 — монтаж фундамента;

3 — завоз металлоконструкций;

4 — монтаж подъемного крана;

5 — монтаж каркаса здания.

На рис. 2.21 изображен сетевой граф некоторого комплекса раб в виде взвешенного графа с указанием времени, затраченного выполнение этой работы (в минутах).

В основе процесса планирования лежит некоторый сценарл представляющий собой сеть, состоящую из вершин — пошагового описания действий и дуг — отношений между ними. Такой дает возможность, сравнивая альтернативы, планировать действия для достижения поставленной цели.

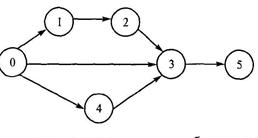
Рис. 2.20. Диаграмма последовательности работ при строительстве здания

Сети широко используются в качестве моделей для представления знаний в интеллектуальных системах. Сетевая модель представления информации основана на том, что любые знания можно рассматривать как множества объектов (понятий) и связи между ними (отношения).

Понятия-объекты и другие элементы предметной области могут быть графически изображены в виде вершин, а отношения между ними — в виде дуг, связывающих эти вершины. Такое физическое представление информации (знаний) в интеллектуальных системах носит название семантических сетей. Они являются универсальным средством для представления знаний в интеллектуальных системах. Понятия, входящие в сети, можно описать с помощью фрейма. Фреймом называется минимально возможное описание сущности некоторого явления, объекта, события процесса. Состоит фрейм из набора стандартных единиц — слотов, содержащих определенный минимум информации о его содержании и назначении. Семантическая сеть в виде некоторой ее совокупности фреймов нуждается в указании отношения междуеевершинами, что тоже возможно осуществить в виде слота. Семантические сети широко применяются в информатике, например, для операций поиска по образцу, где в виде сетей представляется база данных. Результат такого поиска можно изобразить графом. Используются сети и для графической иллюстрации системы отношений базы данных.

Широко применяются сети для графического изображения различных логических схем в теории автоматов, например схемы с памятью, у которых каждый узел F(i) — функция алгебры логики (см., например, рис. 4.17, 4.18).

Для формального описания совокупности процессов, протекающих одновременно, используют сети Петри. Они представляют собой ориентированные графы, состоящие из вершин двух видов: некоторых позиций и переходов, причем позиции изображают кружочками, а переходы — «планками» (рис. 2.22). Сети Петри предназначены для описания действия дискретных процессов во времени. Такие сети дают возможность моделировать ситуации протекания параллельных процессов, прослеживать возможные варианты их взаимодействия, выявлять нежелательные ситуации. Также в виде сетей изображаются схемы устройств, например радиоприемника или телевизора.

Дата добавления: 2014-11-29