Деревья. Лес. Бинарные деревья

С вершины дорога вперед — только вниз.

Я. Таранов

Деревом называют конечный связный граф с выделенной вершиной (корнем), не имеющий циклов (рис. 2.14).

Для каждой пары вершин дерева — узлов — существует единственный маршрут, поэтому вершины удобно классифицировать по степени удаленности от корневой вершины. Расстояние до корневой вершины V ₀ называется ярусом s вершины, s= d (V ₀ V).

Поскольку маршрут между двумя вершинами единственный, то, применяя это свойство к смежным вершинам, можно заключить, что любая ветвь является мостом. Действительно, при удалении ребра этот единственный маршрут прерывается. Тогда граф распадается на два подграфа.

Рис. 2.14. Иллюстрация графа-дерева

В одном из них остается корневая вершина, и этот граф G ₁тоже будет являться деревом. В другом графе 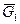выделим вершину, инцидентную удаленному мосту. Тогда второй подграф также будет являться деревом. Если в исходном графе вершина F принадлежала s -му ярусу, а дерево «обрубили» по ребру, соединявшему вершины t -го и (t - 1)-го ярусов, причем s ³ t, то тогда

В_частности, если s = t и FÎ 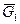, то вершина F будет корневой для 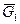и s’ (F)= s - t =0. Если s < t, то вершина заведомо принадлежит подграфу G ₁.

Наиболее характерные свойства деревьев, которые одновременно служат эквивалентными определениями дерева, сформулируем в следующей теореме.

Теорема 2.7. Граф G(V, X) ( ï V ï = п > 1 } является деревом тогда и только тогда, когда выполняется хотя бы одно из условий:

граф G(V, X) связен и не содержит циклов',

граф G(V, X) не содержит циклов и имеет п- 1 ребро;

граф G(V, X) связен и имеет п- 1 ребро;

граф G(V, X) не содержит циклов, но добавление ребра между несмежными вершинами приводит к появлению одного и только одного элементарного цикла;

граф G(V, X) связный, но утрачивает это свойство после удаления любого ребра;

в графе G(V, X) всякая пара вершин соединена цепью, и только одной..

Итак, дерево с п вершинами имеет п - 1 ребро, поэтому оно будет минимальным связным графом. Висячие вершины, за исключением корневой, называются листьями. На рис. 2.14 листьями являются, например, вершины V ₄, V ₁₃ и V ₂₀. При п = 2 дерево состоит из корня и листа и имеет вид отрезка.

Пусть G ₁, G ₂,..-, G _k — непересекающиеся деревья, т.е. " i, j Î (1,..., k), G _i Ç G _j=Æ. Тогда упорядоченное объединение деревьев G = 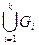, представляет собой несвязный граф, называемый лесом. Компонентами связности леса являются деревья. Остовом связного графа G называется любой его подграф, содержащий все вершины графа G и являющийся деревом (говорят: «покрывающим его деревом»).

Кодеревом Т’ остова T графа G называется дополнение T до G, т. е. такой его подграф, который содержит все его вершины и только те ребра, которые не входят в Т. Тогда G= Т ÈТ' = Т Å Т'. Иначе говоря, кодеревом остова Т(V, Х ₁ ) графа G(V, Х) будет остов Т' (V, Х\Х ₁ ). Очевидна двойственность: (Т')'= Т.

Дерево может быть представлено расслоенным на ярусы (уровни), при этом ветвям, попавшим в один ярус, соответствует одинаковая длина пути исходного графа. Число путей в каждом дереве соответствует числу висячих вершин (листьев). Например, в графе на рис. 2.14 двадцать листьев и двадцать путей от V ₀.

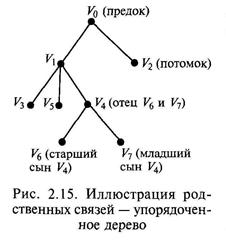При описании деревьев принято использовать термины: отец, сын, предок, потомок.

Каждая вершина дерева называется узлом, причем каждый узел является корнем дерева, имеющего п поддеревьев (п е [0, п)). Тогда узел без поддеревьев называется листом и является висячей вершиной. Узел k -го яруса называется отцом узла (k+ 1)-го яруса, если они смежны. Узел (k+ 1)-го яруса называется сыном узла k-го яруса. Два узла, имеющие одного отца, называются братьями (рис. 2.15). Упорядоченным деревом называется дерево, в котором поддеревья каждого узла образуют упорядоченное подмножество. Для упорядоченных деревьев принята терминология: старший и младший сын для обозначения соответственно первого и последнего сыновей некоторого узла.

В информатике принято использовать подмножество множества деревьев, когда каждый узел либо является листом, либо образует два поддерева: левое и правое. Такой вид деревьев называется бинарными деревьями и используется при делении множества на два взаимоисключающих подмножества по какому-то признаку (так называемое дихотомическое деление). Для отца А — сыновья В и С, причем В — левый, а С — правый потомки. Строго бинарным деревом называется такой граф (рис. 2.16), у которого каждый узел, не являющийся листом, содержит два и только два поддерева — левое и правое.

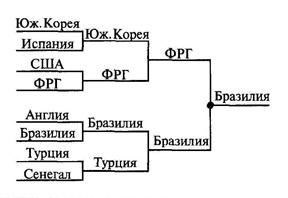
Бинарное дерево уровня п называется полным, если каждый его узел уровня п является листом, а каждый узел уровня меньше, чем п, имеет непустое левое и правое поддеревья. Примером полного бинарного дерева служит таблица розыгрыша соревнования по олимпийской системе («плей-офф»). На рис. 2.17 приведена таблица розыгрыша Кубка мира по футболу 2002 г., начиная со стадии четвертьфиналов (указан корень V₀ — Бразилия).

Бинарные деревья применяются в информатике для поиска одного из двух возможных вариантов ответа. Например, при поиске данных, когда необходимо сравнить каждый элемент списка с образцом, и если значения совпадают, то процесс поиска завершен, а если не совпадают, то поиск данных продолжается. Впервые понятие двоичного дерева ввел в III в. римский философ Порфирий.

Рис. 2.17. Бинарное дерево для представления розыгрыша Кубка мира по футболу 2002 г.

Цикломатическое число графа. Пусть задан неориентированный граф G. Цикломатическим числом графа называется число v(G) = т(G) + с(G) - п(G), где т(G) — число его ребер; с(G) — число связных компонент графа; п(G) — число вершин. Цикломатическое число дерева равно нулю. Цикломатическое число леса равно сумме цикломатических чисел составных связных компонент — деревьев и, следовательно, тоже равно нулю. Для остальных графов цикломатические числа — положительные.

Например, для полного графа К₅ (имеющего пять вершин и С₅² = 10 ребер) Цикломатическое число равно у=10+1-5=6.

Дата добавления: 2014-11-29