Примеры решения типовых задач

О решение задач аналитической геометрии на плоскость и прямую

Чтобы научиться решать задачи на плоскость и прямую надо основательно усвоить разделы линейной алгебры, особенно теорию определителей, методы исследования и решения систем линейных уравнений; элементы векторной алгебры: понятие о векторах, действие над ними, скалярное, векторное и смешанное произведения.

Пример 1. Привести к нормальному виду уравнение плоскости 2x + 3y - 6z + 14 = 0

Решение. Из (6.3) с использованием формулы (6.3.8) находим l = -1/7.

Нормальное уравнение данной плоскости имеет вид

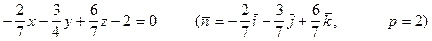
Пример 2. Найти расстояние от точки М₁(1,2,3) до плоскости 2x + y - 3z + 5 = 0

Решение. Из (6.4.) с использованием формулы (6.4.2) находим

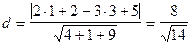
Пример 3. От общего уравнения прямой перейти к каноническому.

Решение. Исключим из системы

переменную x и выразим z через y.

Результат этого действия обозначим через z=(y-y₀)/n₁ (y₀,n₁-числа). Далее из этой же системы исключим y и выразим z через x; пусть этот результат будет 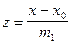(x₀, m₁ - числа).

После этого получим каноническое уравнение прямой в таком виде:

(x-x₀)/m₁ = (y-y₀)/n₁ = z/1

Вывод: данная прямая проходит через точку М₀ (x₀, y₀,0) в направлении вектора
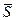(m₁,n₁,1)

Пример 4. Найти проекцию прямой (x-1)/2 = (y+1)/3 = (z-2)/-1 на плоскость 2x-3y-4z+5=0. Уравнения проекции привести к каноническому виду.

Решение. Запишем уравнение данной прямой в виде уравнения двух плоскостей

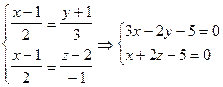
Далее, записываем уравнение пучка плоскостей (6.6): 3x - 2y – 5 + l(x + 2z - 5) = 0. Выбираем из пучка плоскость, перпендикулярную к плоскости 2x - 3y - 4z + 5 = 0.

Для этого используем условие перпендикулярности двух плоскостей (6.5.5)

2(3 + l) + (-3)(-2) + (-4)2l = 0 Þ 12 - 6l=0 Þ l = 2

Подставляя l = 2 в уравнение пучка, находим уравнение проектирующей плоскости:

5x - 2y + 4z - 15 = 0

Таким образом, искомая проекция определяется уравнениями

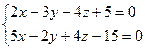
Остаётся эти уравнения привести к каноническому виду. Рекомендуется сделать самостоятельно, используя метод примера 3.

Ответ: (x - 5)/20 = (y - 5)/28 = (-7)/11

Дата добавления: 2014-11-29