Моделі та прогнозних значень залежної змінної

Встановлення інтервалів довіри для параметрів регресійної

Вибіркова регресійна модель утворюється на підставі певної вибірки з генеральної сукупності даних. З однієї генеральної сукупності можна утворити різні вибірки і відповідно побудувати ряд вибіркових регресійних моделей. Постає питання, яка з вибіркових моделей є найближчою до узагальненої моделі, тобто як оцінити відповідність між параметрами вибіркової та узагальненої моделей, чи іншими словами – наскільки теоретичні значення , які розраховані за вибірковою моделлю, будуть близькими до їх математичного сподівання за узагальненою моделлю.

Певні статистичні (ймовірнісні) висновки про значення параметрів можна зробити, при виконанні таких основних припущень:

1. Регресійну модель специфіковано вірно, існуючий зв'язок між ознаками є лінійним.

2. Випадкова величина 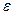розподілена за нормальним законом, має нульове математичне сподівання та дисперсію .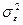

3. Математичне сподівання випадкової величини не залежить від значення та дорівнює нулеві , тобто чинники, які не враховано у моделі, і дія яких проявляється через значення випадкової величини , не впливають систематично на математичне сподівання .

4. Випадкові величини є незалежними між собою, тобто автокореляція між випадковими величинами , відсутня .

5. Дисперсія випадкових величин є сталою для усіх значень . Умовна дисперсія розподілу залежної змінної є також сталою величиною . При виконанні цієї умови випадкові величини є гомоскедастичними, при невиконанні – гетероскедастичними.

Якщо умови (1) - (5) виконуються, то оцінки параметрів узагальненої регресійної моделі будуть BLUE-оцінками: незміщеними - , ; обґрунтованими – при зростанні обсягу вибірки оцінки наближаються до параметрів ; ефективними - , 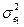набувають мінімальних значень порівняно з будь-якими іншими оцінками параметрів .

Відзначимо також, що при виконанні припущень (1) - (5) отримаємо такі математичні сподівання і дисперсії залежної змінної та параметрів вибіркової регресійної моделі:

1. ; ;

2. ; ;

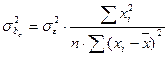3. ; .

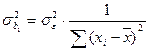Враховуючи, що 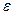- неспостережувана випадкова величина, дисперсію якої встановити неможливо, замінимо на її математичне сподівання (оцінку)

,

що дасть змогу обчислити оцінені дисперсії параметрів :

, (3.22)

. (3.23)

Параметри рівняння регресії розраховують на підставі обмеженої вибірки даних минулих періодів. Водночас їх значення відіграють важливу роль у процесах планування і прогнозування соціально-економічних показників. Дані вибірки можуть вказувати на лінійний характер зв’язку між показниками, хоча насправді в генеральній сукупності він не існує (рис.3.17, 3.18). Тому необхідно визначити ймовірність того, що лінійний зв'язок у вибірковій сукупності свідчить про той же зв’язок у генеральній сукупності, тобто оцінити значущість коефіцієнтів регресії.

– елементи, що увійшли у вибірку

Рис. 3.17. Вибірка, яка відповідає характеру зв'язку між ознаками у генеральній сукупності

Рис. 3.18. Вибірка, яка не відповідає характеру зв'язку між ознаками у генеральній сукупності

Випадкові параметри розподілені за нормальним законом з математичним сподіванням , і дисперсією , 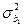. Для знаходження інтервалів довіри параметрів узагальненої моделі, тобто інтервалів, у які із заданою ймовірністю потрапляють значення , першочергово перевіряють значущість параметрів вибіркової моделі за - критерієм Стьюдента (Госсета).

При тестуванні за - критерієм Стьюдента враховують рівень значущості і ступінь вільності . За таблицею - розподілу встановлюють критичне значення - критерію 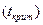, яке поділяє усю множину значень на дві частини – множину, яку відкидають (критичну область), і множину, яку приймають при заданому рівні значущості (рис.3.19).

Рис. 3.19. Двостороння перевірка нульової гіпотези

Послідовність тестування за - критерієм Стьюдента:

1. Формулювання статистичних гіпотез:

, або .

2. Обчислення розрахункових значень - критерію Стьюдента:

, .

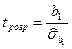3. Встановлення критичних значень - статистики з урахуванням рівня значущості і ступеня вільності за таблицею - розподілу.

4. Перевірка умови :

· якщо умова виконується, то потрапляє у критичну область, нуль-гіпотеза відхиляється, відповідний параметр є статистично значущим;

· якщо умова не виконується, то потрапляє в область значень, які відкидають, нуль-гіпотеза приймається, відповідний параметр є статистично незначущим.

Аналогічно здійснюють тестування значущості коефіцієнта кореляції узагальненої моделі шляхом обчислення розрахункового значення і порівняння його з критичним (див. формулу (3.13)).

Зауважимо, що при спрощеній процедурі тестування використовують умову 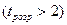- нуль-гіпотезу відхиляють, якщо .

З урахуванням формул (3.22) – (3.23) знаходять граничні похибки коефіцієнтів регресії:

; , (3.24)

де - імовірнісний коефіцієнт, знайдений за таблицею розподілу Стьюдента, для вибраного рівня істотності і ступенів вільності.

Отже, межі довірчих інтервалів коефіцієнтів регресії становлять: , тобто .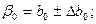

На рис.3.20 наведено геометричну інтерпретацію граничної похибки коефіцієнта регресії . З урахуванням граничної похибки коефіцієнта регресії пряма регресії буде розміщена посередині пари кутів, що утворюються в результаті перетину у точці прямих, кутові коефіцієнти яких дорівнюють 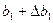і .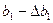

На рис.3.21 наведено геометричну інтерпретацію граничної похибки параметра . З урахуванням пряма регресії буде зміщена паралельно сама собі на величину .

Як відзначалося вище рівняння регресії має імовірнісний характер, тому , де - випадкова величина, яка відображає вплив неврахованих факторів і невідповідність вибіркової сукупності генеральній. З метою забезпечення надійності оцінок взаємозв’язку між статистичними показниками необхідно знайти максимально і мінімально можливі значення випадкової компоненти із заданою ймовірністю, тобто межі довірчого інтервалу.

Рис. 3.20. Геометричний зміст граничної Рис. 3.21. Геометричний зміст граничної

похибки параметра регресії b ₁ похибки параметра регресії b ₀

Якщо зробити припущення, що вибірка була репрезентативною, а відхилення 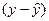розподілені нормально, то можна стверджувати, що ймовірність перебування фактичних значень залежної змінної ознаки в певних межах дорівнює:

. (3.25)

Величина характеризує непояснену варіацію фактичних значень відносно розрахункових . Непояснена варіація характерна для будь-якої сукупності (вибіркової чи генеральної) при існуванні кореляційного зв'язку.

У практиці прогнозування знаходять інтервали довіри для середнього та індивідуального значень залежної змінної ознаки при заданому значенні , які відповідно дорівнюють:

, (3.26)

. (3.27)

Як видно із (3.26), (3.27) і рис.3.20, 3.21 інтервали довіри для середнього та індивідуального значень залежної змінної ознаки залежить від значення .

Користуючись методом найменших квадратів, після нескладних математичних перетворень можна отримати системи лінійних рівнянь для визначення невідомих параметрів рівняння нелінійної регресії.

Наведемо приклади зведення деяких нелінійних функцій до лінійного вигляду:

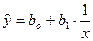• , , де ;

• , , де ;

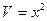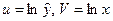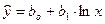• , де ;

• , , де ;

• , де .

Приклад 3.2. За даними табл.3.3 необхідно оцінити щільність лінійного зв’язку між показниками, побудувати рівняння парної регресії, що описує залежність між обсягом випущеної продукції і вартістю виробничих фондів, а також перевірити значущість отриманих результатів.

За незалежну (факторну) ознаку приймемо вартість виробничих фондів, а за результативну – обсяг випущеної продукції. Для розрахунку шуканих параметрів скористаємося методом найменших квадратів. Результати проміжних розрахунків представлено у табл.3.4.

Таблиця 3.3

№ спосте-реження	Обсяг випущеної продукції, тис.грн.	Вартість виробничих фондів, тис.грн.	№ спосте-реження	Обсяг випущеної продукції, тис.грн.	Вартість виробничих фондів, тис.грн.
	11,6	3,7		14,5	7,0
	15,5	8,1		11,8	3,9
	18,1	9,7		17,7	9,3
	15,1	7,1		12,2	5,0
	10,1	3,0		14,0	5,5
	15,2	7,5		19,3	10,4
	16,1	8,4		19,9	10,6
	15,6	8,0		14,6	7,7
	14,1	5,6		15,5	7,0

Таблиця 3.4

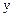
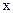
11,6	3,7	42,92	134,56	13,69	11,20647	0,154869	14,77275	11,44694
15,5	8,1	125,55	240,25	65,61	16,20495	0,496959	1,333918	1,033611
18,1	9,7	175,57	327,61	94,09	18,02259	0,005993	8,836263	6,846944
15,1	7,1	107,21	228,01	50,41	15,06893	0,000965	0,000358	0,000278
10,1	3,0	30,3	102,01		10,41125	0,096878	21,51798	16,67361
15,2	7,5		231,04	56,25	15,52334	0,10455	0,224052	0,173611
16,1	8,4	135,24	259,21	70,56	16,54576	0,198702	2,237296	1,733611
15,6	8,0	124,8	243,36		16,09135	0,241426	1,084413	0,840278
14,1	5,6	78,96	198,81	31,36	13,3649	0,540366	2,839549	2,200278
14,5	7,0	101,5	210,25		14,95533	0,207327	0,008962	0,006944
11,8	3,9	46,02	139,24	15,21	11,43367	0,134198	13,07784	10,13361
17,7	9,3	164,61	313,29	86,49	17,56818	0,017377	6,341217	4,913611
12,2	5,0		148,84		12,68329	0,233571	5,601307	4,340278
14,0	5,5			30,25	13,2513	0,560549	3,235315	2,506944
19,3	10,4	200,72	372,49	108,16	18,8178	0,232518	14,19631	11,00028
19,9	10,6	210,94	396,01	112,36	19,045	0,73102	15,96005	12,36694
14,6	7,7	112,42	213,16	59,29	15,75055	1,323755	0,490764	0,380278
15,5	7,0	108,5	240,25		14,95533	0,296664	0,008962	0,006944
270,9	127,5	2017,26	4194,39	989,73	270,9	5,577686	111,7673	86,605

Із табл.3.4 маємо:

,

,

Тоді середні значення результативної і факторної ознак відповідно рівні:

;

.

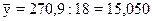Згідно (3.12) обчислюємо коефіцієнт кореляції:

.

Знайдене значення коефіцієнта кореляції вказує на дуже щільний зворотний зв'язок між обсягом випущеної продукції і вартістю виробничих фондів.

Для перевірки значущості коефіцієнта кореляції скористаємося -критерієм Стьюдента. За допомогою (3.13) знаходимо розрахункове значення критерію:

.

З таблиці значень функції розподілу Стьюдента для ймовірності 0,950 і ступеня вільності , отримуємо 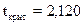. Оскільки , то можна стверджувати, що існування кореляційного зв’язку між досліджуваними показниками підтверджується.

Користуючись проміжними значеннями розрахунку коефіцієнта кореляції та співвідношеннями (3.20) і (3.21), обчислюємо значення параметрів рівняння лінійної регресії :

;

.

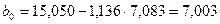Отже, рівняння регресії має вигляд:

.

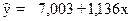Для оцінки адекватності лінійної регресійної моделі застосуємо -критерій Фішера.

Розрахункове значення -критерію дорівнює:

.

При рівні значущості 95% і і ступенях вільності з таблиці розподілу функції Фішера знаходимо . Розрахункове значення критерія перевищує табличне, отже, гіпотеза про значущість рівняння регресії підтверджується.

Середня квадратична похибка залишків буде становити:

.

Допустимо, що у прогнозному періоді вартість виробничих фондів планується на рівні . Тоді обсяг випущеної продукції буде становити:

(тис.грн.).

З імовірністю 0,950 можна стверджувати, що для прогнозні значення обсягну випущеної продукції будуть знаходитися у таких межах:

,

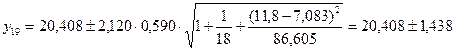або

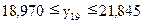(тис.грн.).

Користуючись середніми значеннями фактичних даних і обчисленим значенням коефіцієнта регресії, знаходимо коефіцієнт еластичності:

.

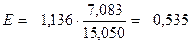Із збільшенням вартості виробничих фондів на 1% обсяг випущеної продукції збільшиться у середньому на 0,535%.

Практичне використання сформульованого вище висновку вимагає перевірки значущості коефіцієнта регресії і визначення його області зміни.

Знайдемо оцінку середнього квадратичного відхилення параметра регресії :

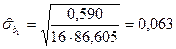
Значення для параметра буде становити:

.

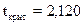Для ймовірності 0,950 і ступенях вільності розрахункове значення критерію Стьюдента () перевищує критичне (), тому висновки, зроблені на основі коефіцієнта регресії, можна вважати правильними.

Довірчі границі параметра регресії становлять:

,

З ймовірністю 0,950 можна вважати, що коефіцієнт еластичності знаходиться в межах

.

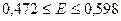Отже, можна зробити висновок, що отримані результати моделювання є істотними і можуть служити основою прогнозування обсягів виробництва залежно від вартості наявних виробничих фондів.

Дата добавления: 2014-12-16