
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Короткое замыкание
|
|
|
|
Из закона Ома для полной цепи следует, что сила тока в цепи с заданным источником тока зависит только от сопротивления внешней цепи R.
Если к полюсам источника тока подсоединить проводник с сопротивлением R<< r, то тогда только ЭДС источника тока и его сопротивление будут определять значение силы тока в цепи. Такое значение силы тока будет являться предельным для данного источника тока и называется током короткого замыкания.
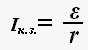
18.Закон Ома для однородного участка цепи. Закон ома в дифференциальной форме.
Ом экспериментально установил закон, согласно которому сила тока, текущего по однородному металлическому проводнику, пропорциональна падению напряжения U на проводнике:
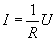
| (17.5) |
Однородным называется участок цепи, в котором не действуют сторонние силы.
Величина R называется электрическим сопротивлением проводника. Единицей сопротивления служит Ом, равный сопротивлению такого проводника, в котором при напряжении 1В течет ток в 1 А.
Величина сопротивления зависит от формы и размеров проводника, а также от свойств материала, из которого он сделан. Для однородного цилиндрического проводника.
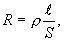
где  - длина проводника, S - площадь поперечного сечения,
- длина проводника, S - площадь поперечного сечения, 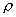 - зависящий от свойств материала коэффициент, называемый удельным электрическим сопротивлением вещества.
- зависящий от свойств материала коэффициент, называемый удельным электрическим сопротивлением вещества.
Величина обратная сопротивлению называется проводимостью

Для большинства металлов удельное сопротивление растет с температурой приблизительно по линейному закону.
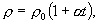
где  - удельное сопротивление при 0°С, t - температура в градусах Цельсия,
- удельное сопротивление при 0°С, t - температура в градусах Цельсия,  - постоянный коэффициент, численно равный примерно 1/273.Закон Ома можно записать в дифференциальной форме. Выделим в проводнике элементарный цилиндрический объем dV с образующими, dl параллельными вектору плотности тока
- постоянный коэффициент, численно равный примерно 1/273.Закон Ома можно записать в дифференциальной форме. Выделим в проводнике элементарный цилиндрический объем dV с образующими, dl параллельными вектору плотности тока  в данной точке (рис. 17.2). Через поперечное сечение dS цилиндра течет ток силой
в данной точке (рис. 17.2). Через поперечное сечение dS цилиндра течет ток силой  . Напряжение, приложенное к цилиндру, равно
. Напряжение, приложенное к цилиндру, равно 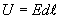 , где Е - напряженность поля в данном месте. Сопротивление цилиндра
, где Е - напряженность поля в данном месте. Сопротивление цилиндра  . Подставив эти значения в уравнение (17.5), получим
. Подставив эти значения в уравнение (17.5), получим
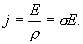

Носители заряда в каждой точке движутся в направлении вектора  . Поэтому направления векторов
. Поэтому направления векторов  и
и  совпадают. Таким образом, можно написать
совпадают. Таким образом, можно написать

| |||
| Закон Ома в дифференциальной форме |  
| ||
Закон Ома в интегральной форме для однородного участка цепи (не содержащего ЭДС)
Для однородного линейного проводника выразим R через ρ:
ρ – удельное объемное сопротивление; [ρ] = [Ом·м]. Найдем связь между В изотропном проводнике (в данном случае с постоянным сопротивлением) носители зарядов движутся в направлении действия силы, т.е. вектор плотности тока
Рис. 7.6 Исходя из закона Ома (7.6.1), имеем:
А мы знаем, что
это запись закона Ома в дифференциальной форме. Здесь Размерность σ – [ Плотность тока можно выразить через заряд электрона е, количество зарядов n и дрейфовую скорость
Обозначим
Теперь, если удельную электропроводность σ выразить через е, n и b:
|
19.Зависимость сопротивления от температуры. Явление сверхпроводимости.
|
|
|
|
|
Дата добавления: 2014-12-16; Просмотров: 523; Нарушение авторских прав?; Мы поможем в написании вашей работы!

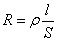 ,
,
 и
и  в бесконечно малом объеме проводника – закон Ома в дифференциальной форме.
в бесконечно малом объеме проводника – закон Ома в дифференциальной форме.
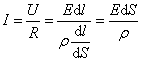
 или
или  . Отсюда можно записать
. Отсюда можно записать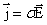 ,
,
 – удельная электропроводность.
– удельная электропроводность. ].
]. :
: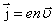 .
. , тогда
, тогда  ;
;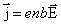
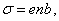 то вновь получим выражение закона Ома в дифференциальной форме:
то вновь получим выражение закона Ома в дифференциальной форме: