Моделювання тенденції динамічного ряду

Однією із задач моделювання ряду динаміки є виділення основної тенденції зміни рівнів, яка дасть можливість простежити загальну закономірність розвитку досліджуваного явища або процесу. Основну тенденцію виявляють на підставі аналізу наявного статистичного матеріалу. Графічний аналіз даних дає змогу зробити певні припущення щодо тенденції зміни рівнів ряду. Однак більшість даних економічного характеру містять природні випадкові флуктуації або “шуми”, тому дослідження тенденції графічними методами не завжди закінчується успіхом. Потрібні засоби, за допомогою яких можна вилучити ефект дії випадкових флуктуацій, що дасть змогу оцінити характеристики динамічного ряду, необхідні для побудови економіко-статистичної моделі.

Найпоширеніші такі способи визначення основної тенденції динамічного ряду:

• укрупнення інтервалів;

• розрахунок середніх плинних;

• аналітичне вирівнювання.

Сутність способу укрупнення інтервалів полягає у заміні початкового ряду динаміки іншим, показники якого відображають явище за більш тривалий період. Новоутворений ряд може містити абсолютні або середні величини. Внаслідок укрупнення інтервалів відхилення, які викликані дією випадкових факторів, поглинаються (елімінуються).

Елімінувати випадкові коливання і отримати значення, що є результатом дії основних факторів, можна і замінивши первісний динамічний ряд рядом середніх плинних (ковзних). Для розрахунку середніх плинних спочатку знаходять середнє арифметичне значення m перших рівнів ряду і відносять його до середини вибраного періоду. Після цього період зміщують на одне спостереження і обчислюють середнє значення рівнів з порядковими номерами 2, 3,..., m+1. Далі період знову зсувають на одне спостереження і знаходять нову середню плинну. Кожен раз знайдену середню відносять до середини укрупненого інтервалу.

Вибір інтервалу згладжування (інтервалу, для якого знаходять середні) залежить від цілей дослідження. Насамперед необхідно керуватися метою усунення впливу випадкових факторів.

Ряд плинних середніх коротший від первісного на (m-1) рівнів. Якщо кількість рівнів інтервалу згладжування парна, знайдена середня плинна не ставиться у відповідність жодному з рівнів динамічного ряду, а відноситься до середини між двома крайніми датами.

Приклад 5.3. За даними про щомісячний випуск продукції підприємством виконати вирівнювання ряду динаміки, застосовуючи способи укрупнення інтервалів та плинної середньої.

Місяць

Кількість, тис.шт.

Результати укрупнення періодів наведено у табл.5.6.

Таблиця 5.6

Показники	І кв.	ІІ кв.	ІІІ кв.	ІV кв.
Кількість випуску продукції, тис.шт.
Середньомісячний випуск продукції, тис. шт.

За плинний інтервал виберемо п’ять місяців. Ряд фактичних рівнів і відповідних їм середніх плинних наведено у табл.5.7.

Таблиця 5.7

Місяць
Кількість випуску продукції, тис. шт.
Плинні середні, тис. шт.	-	-	247,4	251,4	254,0	257,0	261,2	264,4	267,4	270,6	-	-

Ряд плинних середніх, як і ряд квартальних середніх, поданих відповідно у табл.5.6 і 5.7, вказує на явно виражену тенденцію до зростання виробництва.

Вага кожного елемента ряду динаміки під час обчислення середньої вказує на частку його внеску у значення середньої. Дані, які використовують для обчислення плинної середньої, мають одинакові ваги, що можна вважати недоліком, оскільки для дослідження багатьох економічних процесів нові дані є ціннішими, а, отже повинні мати більшу вагомість для визначення основної тенденції. Застосування середніх плинних з однаковими вагами може призвести до погашення не тільки випадкових, а й притаманних процесу періодичних коливань. Вказаний недолік усувають, застосовуючи методи усереднення з різними вагами. Найпоширенішим методом вирівнювання рядів динаміки з використанням різних ваг є метод експоненційної середньої.

Для обчислення експоненційних середніх використовують послідовність ваг, які спадають в часі:

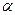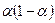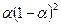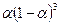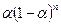; ; ; ; …; , де 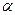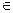(0;1). (5.17)

Оскільки значення 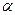лежить у межах від нуля до одиниці, то при збільшенні числа доданків сума вагових коефіцієнтів прямує до 1. Вагова функція формується із урахуванням ступеня новизни інформації, а експоненційну середню обчислюють згідно з виразом:

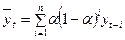, (5.18)

де 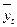– експоненційна середня (згладжене значення рівня) на момент t;

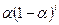– вага 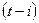-го рівня динамічного ряду.

Розклавши (5.18) за елементами суми, отримаємо:

,

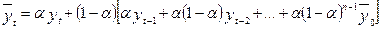або

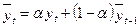
Отже, експоненційну середню для моменту часу t визначають як лінійну комбінацію значення t-го рівня динамічного ряду та експоненційної середньої 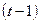-го моменту часу.

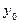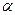Розрахунок експоненційної середньої вимагає вказання початкових умов, а саме значень і . Як 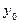можна використати середній рівень за минулий (до динамічного ряду) період, або, у разі відсутності таких даних, необхідно прийняти 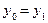. Стосовно вибору 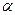існує декілька практичних рекомендацій, але завжди треба враховувати, що від коефіцієнта 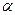залежить чутливість і стійкість експоненційної середньої. Чим більше значення 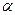, тим чутливішою є експоненційна середня до останніх рівнів динамічного ряду. Чим менше значення 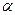, тим експоненційна середня є стійкішою. Для економічних досліджень рекомендують вибирати 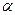в межах від 0,05 до 0,3.

Під час аналітичного вирівнювання фактичні рівні динамічного ряду замінюють теоретичними, розрахованими, як правило, на підставі рівняння регресії. Час розглядається як незалежна змінна, а рівні ряду як функція цієї змінної 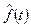. Вибір виду функції, яка найкраще відображає основну тенденцію, вважається однією із найважливіших проблем моделювання динаміки. Невдало визначена форма кривої може призвести до гірших наслідків, ніж помилка, яка допущена під час статистичного оцінювання параметрів моделі.

Підбір виду функції здійснюють з урахуванням специфіки досліджуваного процесу і характеру динаміки. Найпростіший шлях вибору форми кривої, яка апроксимує реальний процес, - візуальний аналіз графічного подання динамічного ряду. Після вибору форми лінії регресії оцінюють її параметри, використовуючи найчастіше метод найменших квадратів.

На практиці переважно використовують функції, параметри яких мають змістовну інтерпретацію (абсолютну швидкість зміни рівнів ряду, приріст абсолютної швидкості тощо).

Найпростішим вважається лінійний тренд, рівняння якого має вигляд:

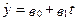(5.19)

Лінійний тренд використовують для описання процесів, які рівномірно змінюються у часі і мають постійний приріст 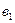за початкового рівня .

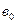Поліном другого порядку (параболу)

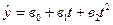(5.20)

використовують для описання процесів, характерною особливістю яких є рівноприскорене зростання або спадання рівнів. Тоді параметр 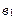характеризує постійну швидкість зростання, а 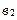– постійну швидкість зміни приросту (пришвидшення зростання).

У загальному випадку для описання тренду можна використати поліном р-го порядку:

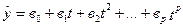(5.21)

Порядок полінома можна визначити за допомогою методу послідовних різниць, зміст якого полягає у знаходженні перших, других та інших різниць рівнів ряду динаміки:

;

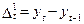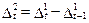; (5.22)

.

Розраховують різниці доти, доки вони не стануть приблизно рівними, а їхній порядок приймають за порядок шуканого полінома.

Тренд динамічного ряду із порівняно стабільними темпами приросту доцільно подавати у формі експоненти (5.23) або модифікованої експоненти (5.24):

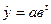; (5.23)

. (5.24)

Функцію (5.23) використовують для дослідження процесів з постійним темпом зростання і постійним темпом приросту. Якщо в>1, то із збільшенням t крива зростає, а при в<1 – спадає. Логарифмуючи праву і ліву частини (5.23), отримуємо лінійну залежність від часу:

,

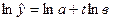параметри якої можна знайти за допомогою методу найменших квадратів.

Модифіковану експоненту (5.24) застосовують для описання економічних процесів, які обмежені знизу. Якщо в>1, вона спочатку повільно, а потім швидко зростає. Якщо в<1, то модифікована експонента спочатку швидко, а потім повільно спадає і обмежена знизу значенням с.

Модифіковану експоненту не вдається привести до лінійного виду, проте існують наближені методи знаходження невідомих параметрів а, в і с, зокрема, метод трьох точок.

Допустимо, що задано ряд динаміки у₁, у₂,..., у_Т. Реалізація методу трьох точок полягає у виконанні таких трьох етапів:

1. Рівні ряду динаміки розділяють на три підмножини за такими правилами:

• якщо величина Т є кратною 3, тобто 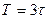, то до кожної із підмножин входить по 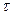рівнів: до першої підмножини – рівні 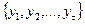, до другої – рівні 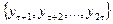, а до третьої - ;

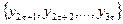• якщо 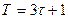, то першу підмножину утворюють рівні 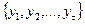, другу – 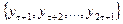і третю - ;

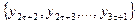• якщо 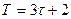, то першу підмножину утворюють рівні 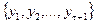, другу - 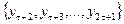і третю - .

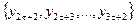2. Для кожної із підмножин обчислюємо значення медіан, які відповідно позначаємо 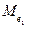, 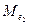і .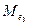

3. Розв’язуємо систему трьох рівнянь з трьома невідомими:

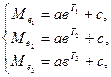
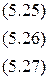
де Т₁, Т₂ і Т₃ – моменти (періоди часу), що відповідають медіанним рівням.

Для знаходження розв’язку системи нелінійних рівнянь (5.25) – (5.27) спочатку визначаємо різниці між рівняннями (3.27) і (3.26) і між рівняннями (5.26) і (5.25):

; (5.28)

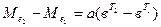. (5.29)

Поділивши (5.28) на (5.29) і враховуючи, що 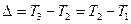, отримаємо:

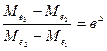, (5.30)

звідки 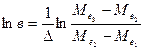(5.31)

Із (5.31) знаходимо в, підставляємо його в (5.28) і одержуємо невідоме значення параметра а:

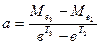. (5.32)

Значення параметра с знаходимо із (3.25):

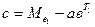(5.33)

Для деяких економічних процесів характерна така динаміка:

· початковий період – досить повільне зростання;

· проміжний період - прискорене зростання;

· завершальний період – уповільнення зростання і наближення до рівня насичення.

Прикладом кривої, яку використовують для моделювання маркетингових (зокрема, описання повного циклу товару) і демографічних процесів, є крива Гомперця:

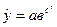, (5.34)

або

.

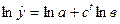Якщо 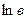< 0 і с < 1, то на першому етапі приріст функції незначний і повільно збільшується із зростанням t, на другому – швидко збільшується, а після досягнення точи перегину повільно наближається до асимптотичної прямої.

Для моделювання процесів з насиченням широко застосовують логістичні криві такого вигляду:

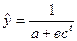• (крива Перля-Ріда); (5.35)

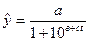• . (5.36)

Вирівнювати ряд динаміки за кривою (5.34) рекомендують, коли перші різниці змінюються з постійним темпом. Якщо ж розподіл різниць першого порядку близький до нормального, то краще скористатися логістичними кривими.

Оцінювання параметрів кривої (5.34) і логістичних кривих можна виконати на основі нелінійної регресії за допомогою ітеративної процедури мінімізації суми квадратів помилок, або скористатися простішими методами (наприклад, методом трьох точок).

Моделювання трендів можна здійснити з використанням ще деяких інших видів кривих, форму яких вибирають на підставі теоретичного аналізу змісту досліджуваного процесу. Але треба зауважити, що для аналітичного вирівнювання рядів динаміки недоцільно вибирати функції з великою кількістю параметрів (особливо при малих обсягах вибірки), оскільки у такому разі трендове рівняння може відображати не основну тенденцію процесу, а випадкові коливання.

Умовами правильного вибору рівняння тренду вважають такі:

• відхилення фактичних рівнів ряду динаміки від обчислених на підставі рівняння тренду (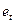) мають випадковий характер;

• відхилення 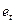підпорядковуються нормальному закону розподілу.

Для перевірки першої умови можна скористатися критерієм серій, реалізація якого передбачає виконання таких кроків:

1. На основі фактичних рівнів ряду динаміки 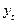і розрахункових 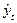знаходять відхилення 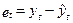, які розташовують у варіаційному ряді за зростанням.

2. Для побудованого варіаційного ряду розраховують медіану .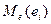

3. Для динамічного ряду 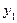, ,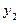…, 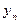визначають послідовність знаків “+” і “-” за умовою:

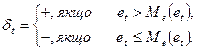(5.37)

4. Підраховують загальну кількість серій V. Під серією розуміють послідовність підряд розташованих знаків “+” або “-”. Серія може складатися тільки із одного знака, тоді її довжина рівна 1. У разі стохастичної незалежності відхилень послідовність не повинна містити довгих серій знаків.

5. Визначають обсяг найдовшої серії .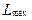

6. Відхилення від тренду вважається випадковим (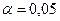), якщо виконуються нерівності:

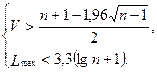(5.38)

Перевірку того факту, що відхилення 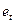є нормально розподіленими, здійснюють на підставі вибіркових оцінок показників асиметрії, ексцесу та їхніх середніх квадратичних похибок (цей матеріал розглядається у курсі “Статистика”)

Дата добавления: 2014-12-16