Багатофакторні економіко-статистичні моделі динаміки

Дослідження зв’язків між взаємопов’язаними у часі явищами передбачає застосування багатофакторного аналізу динаміки. Багатофакторні моделі динаміки будують на основі динамічних рядів, рівні яких стосуються однакових періодів або моментів часу. Інформаційною базою побудови рівняння множинної регресії є просторово-часові вибірки – дані про значення ознак сукупності окремих об’єктів за декілька періодів. Основним інструментом моделювання взаємозв’язаних рядів динаміки слугує кореляційний і регресійний аналіз.

Існує декілька способів побудови рівняння множинної регресійної моделі для аналізу взаємозв’язаних рядів динаміки:

• побудова моделі за рівнями динамічних рядів;

• побудова моделі за відхиленнями фактичних рівнів динамічних рядів від рівнів, вирівняних за трендовими рівняннями;

• побудова моделі за різницями між рівнями динамічних рядів;

• побудова моделі за відхиленнями рівнів динамічних рядів від середнього рівня;

• включення до моделі фактора часу як незалежної змінної.

Лінійна регресійна модель, побудована за результативними () і факторними () рівнями динамічних рядів, у загальному випадку має вигляд:

, (5.51)

де m – кількість факторів, що входять до моделі.

Модель реально відображає вплив факторних ознак на результативний показник лише у разі виконання певних умов, серед яких виділяють відсутність мультиколінеарності між факторними ознаками та автокореляції.

Нагадаємо, що мультиколінеарність– це наявність лінійної або високої кореляційної залежності між двома або декількома факторами, що входять до регресійної моделі. Вона призводить до серйозних проблем, пов’язаних із труднощами обчислювального характеру під час визначення оцінок коефіцієнтів рівняння регресії, із виділенням істотних факторів, спотворенням змісту коефіцієнтів регресії під час спроби їхньої економічної інтерпретації. Встановлення факту існування мультиколінеарості на множині факторних ознак розглянуто у попередньому розділі посібника, а встановлення причин існування мультиколінеарності вимагає детального економічного аналізу суті явища. Найчастіше для послаблення або усунення мультиколінеарності використовують такі прийоми:

• вилучення з моделі однієї або декількох факторних ознак, що є мультиколінеарними між собою, на підставі глибокого змістовного аналізу явища;

• агрегування мультиколінеарних факторів в одну узагальнювальну оцінку;

• побудова рівняння регресії за відхиленнями від тренду або за кінцевими різницями (моделі (5.52) і (5.53)).

Для рядів динаміки, що описують зміну економічних показників у часі, характерною є залежність послідовних спостережень, тобто між рівнями ряду існує автокореляція. Метод найменших квадратів передбачає незалежність спостережень за однією і тією самою змінною. Тому у разі автокореляції оцінки коефіцієнтів рівняння регресії, знайдені методом найменших квадратів, можуть залишатися незміщеними, але будуть неефективними, що ускладнює побудову довірчих інтервалів, перевірку значущості коефіцієнтів регресії. Основними причинами існування автокореляції у випадкових залишках рівняння регресії, побудованого на базі багатовимірних динамічних рядів, є такі:

• в моделі не врахований істотний фактор (його вплив буде відображатися на величині відхилень);

• до моделі не включено декілька факторів, кожний з яких не має істотного впливу на результативний показник, але у разі збігу змін цих факторів за напрямом і фазою у відхиленнях може виникнути автокореляція;

• не враховані особливості внутрішньої структури випадкової компоненти;

• неправильно вибрана форма зв’язку між результативним показником і факторами, що його зумовлюють.

Усунення або зменшення автокореляції можна досягти виключенням із кожного динамічного ряду трендів, які є причиною автокореляції. В загальному випадку модель, яка побудована за відхиленнями фактичних рівнів рядів динаміки від їхніх трендових значень, має вигляд:

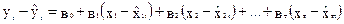, (5.52)

де 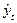та 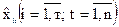– відповідно тенденції результативної і факторних ознак.

Якщо рівні динамічних рядів мають дуже слабку тенденцію або коливаються біля середньої, то можна побудувати модель за відхиленнями рівнів рядів динаміки від їхніх середніх значень, замінивши в (5.52) 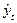і 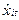відповідно на 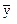і . Проте у разі чітко вираженої тенденції динамічних рядів такий підхід є неправомірним.

Для зменшення автокореляції можна побудувати модель залишкової регресії за різницями між рівнями рядів динаміки:

(5.53)

Передбачається, що всі різниці між рівнями рядів динаміки, починаючи з першої, містять тільки випадкову компоненту. Крім того, вважається, що перші різниці містять випадкову компоненту у лінійній формі, другі – описуються параболою другого порядку, треті – показниковою функцією. Якщо під час дослідження виявиться, що залишкова регресія є сильно корельованою, то (5.53) не можна використовувати для моделювання взаємозв’язаних рядів динаміки.

Іншим способом вилучення автокореляції може слугувати включення до моделі множинної регресії як аргумента часу t:

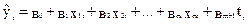, (5.54)

Множинна регресія з відхиленнями від лінійної тенденції вважається еквівалентною (5.54), а коефіцієнт 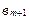в (5.54) можна інтерпретувати як середній приріст результативного показника за одиницю часу (день, місяць, рік) під впливом зміни неідентифікованих у моделі факторів, які рівномірно змінюються в часі.

Розглянуті вище багатофакторні моделі значно розширяють можливості традиційного економічного аналізу і відіграють важливу роль у економічних дослідженнях. Проте вони не враховують зміни, які відбуваються в характері взаємозв’язків між результативною і факторними ознаками в часі, а тому їх не можна використати для моделювання динамічних закономірностей і виявлення тенденцій. Моделі типу (5.51) – (5.54) називають статичними моделями. Передбачення тенденції розвитку результативного показника вимагає побудови багатофакторних динамічних моделей.

Існують різні трактування багатофакторної динамічної моделі, але найповнішим, на нашу думку, є таке. Багатофакторна модель називається динамічною, якщо в ній відображені:

• загальні закономірності зміни результативного показника впродовж досліджуваного періоду часу;

• зміни впливу факторних ознак на результативний показник у часі;

• запізнення впливу факторів у часі.

Остання умова використовується у моделюванні, коли причина і наслідок розділені у часі (наприклад, уведення в дію виробничих потужностей і максимальний ефект від їхньої віддачі). Для оцінювання ефектів таких впливів до моделі необхідно включати лагові змінні.

В загальному випадку динамічну модель з урахуванням лагу 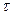можна записати у вигляді:

. (5.55)

Допустимо, що є статистичні дані про значення результативного показника 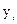і факторних ознак 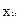, ,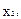…, 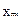для N об’єктів за n періодів і виконуються такі умови:

• функціонування об’єктів характеризується певною інерційністю, яка полягає в тому, що закономірності їхнього розвитку є достатньо стійкими впродовж спостережуваного періоду часу і, постійно еволюціонуючи, будуть зберігатися ще деякий час;

• моделювання здійснюється для великої сукупності об’єктів.

Тоді побудова багатофакторної динамічної моделі, яку прийнято називати просторовою динамічною моделлю зв’язків показників, полягає у виконанні таких процедур:

• будується статична модель, яка складається з n рівнянь регресії, які описують залежність між результативним показником і факторними ознаками для кожного періоду t:

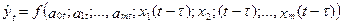; (5.56)

• на підставі значень часових рядів 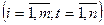знаходять трендові значення 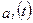, які відображають тенденції, що є наслідком зміни в часі як структур впливу факторів на результативний показник, так і значень самих факторів.

Побудову моделей необхідно здійснювати тільки для однорідних статистичних сукупностей. Розрізняють просторову і часову однорідність. Перша трактується у розумінні близькості (схожості) внутрішніх структур зв’язків між показниками різних об’єктів в однакові періоди часу, а друга – у близькості внутрішніх структур окремого об’єкта у різні періоди. Якщо статистична сукупність є неоднорідною, то отримані в результаті моделювання залежності можуть істотно відрізнятися від реальних. Неоднорідність сукупності може зумовлюватися як відмінністю внутрішніх структур зв’язків окремих об’єктів, так і впливом істотних неврахованих у моделі факторів (наприклад, різні середні значення неврахованих факторів).

Задовільна оцінка якості побудованих моделей може слугувати критерієм достатньої для потреб дослідження однорідності сукупності об’єктів. Наявність кластерів об’єктів в ознаковому просторі дає підставу зробити припущення про існування різних закономірностей зв’язку для окремих груп об’єктів, тобто про неоднорідність сукупності. Підтвердженням цього припущення буде відмінність групових моделей, кожна з яких характеризується достатньо високою якістю.

Адаптування регресійних моделей до неоднорідних сукупностей може відбуватися за рахунок введення до моделей структурних змінних. Якщо статистична сукупність розбита на K кластерів, то кожний з них розглядається як градація номінальної ознаки. Структурними прийнято називати змінні 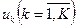, які набувають значення , якщо одиниця сукупності (об’єкт)належить до k-ї градації, і – у протилежному разі. Присвоєння числових значень номінальним ознакам-кластерам має відбуватися тільки за умов повноти шкали градацій і неповторюваності градацій. Якщо виділено K кластерів, то до моделі включається (К-1) структурна змінна, а матриця однакової множини розширяється за рахунок введення матриці структурних змінних 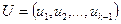. Коефіцієнт регресії при структурній змінній 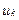буде характеризувати різницю між значенням результативного показника для k –го об’єкта та значенням результативного показника в сукупності загалом.

Для побудови багатофакторної динамічної моделі одного об’єкта період n розділяють на h інтервалів, для кожного з яких висувається гіпотеза про часову однорідність структури зв’язків на інтервалі. Після цього розраховують параметри регресійних рівнянь, які описують залежність між результативним показником і факторами для кожного інтервалу. Застосувавши методи вирівнювання рядів, можна отримати оцінки трендових значень коефіцієнтів рівняння регресії.

Кількість інтервалів h повинна бути достатньо великою, інакше ряди коефіцієнтів рівняння регресії не забезпечать правильного відображення тенденції зміни впливу факторів на результативний показник. Крім того, кількість рівнів, що входять до одного інтервалу, повинна, щонайменше, у 5-6 разів перевищувати кількість незалежних змінних у рівнянні регресії. Тому практична реалізація багатофакторних динамічних моделей ускладнюється, як правило, обмеженістю інформаційної бази.

Необхідною умовою практичного застосування динамічної економіко-статистичної моделі вважається її адекватність. Під адекватністю моделі розуміють відповідність моделі реально існуючому явищу (процесу), яка полягає у здатності правильно відображати структуру залежності результативного показника від факторів, що його зумовлюють.

Дослідження адекватності моделі здійснюється за допомогою змістовного аналізу механізму формування явища і застосування формальних процедур оцінки очікуваної точності моделі і перевірки припущень щодо виконання статистичних умов, необхідних для застосування методів оцінки параметрів моделі. Мірою адекватності моделі вважається розбіжність між фактичними і розрахунковими значеннями результативного показника, а величину розбіжності формує такий комплекс умов:

• інформативність введених до моделі факторів стосовно результативного показника;

• стабільність неврахованих у моделі факторів;

• обсяг та однорідність сукупності;

• достовірність інформації;

• вибрана форма моделі.

Дата добавления: 2014-12-16