ПЛОЩИНА 1 страница

4.1 Способи задання площини та класифікація площин

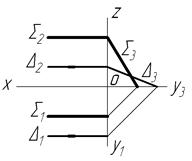
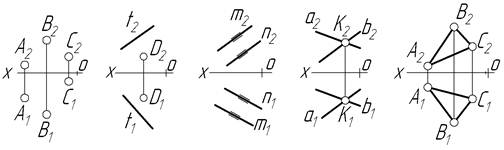На епюрі площина задається проекціями трьох точок, що не лежать на одній прямій, проекціями прямої і точки, яка лежить поза нею, проекціями паралельних прямих, проекціями прямих, що перетинаються, плоскою фігурою (рис.4.1).

Рисунок 4.1 – Задання площини на епюрі

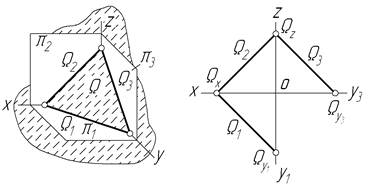Площину на епюрі можна задати ще слідами. Це, фактично, метод задання двома прямими, що перетинаються, до того ж, це прямі особливого положення, оскільки вони лежать на площинах проекцій.

Рисунок 4.2 – Площина загального положення

Слідом площини називають пряму лінію, по якій площина перетинається з площиною проекцій.

Точкою збігу слідів називають точку перетину площини з віссю проекцій. Це точка на площині з однією координатою, бо дві інші дорівнюють нулю. Положення площин у просторі характеризуються їх розміщенням відносно площин проекцій. У зв’язку з цим розрізняють площини довільного положення і особливого.

Площина довільного (або загального) положення – це площина, не перпендикулярна і не паралельна жодній із площин проекцій (рис. 4.2).

Площина проекційна – це площина, яка перпендикулярна до однієї з трьох площин проекцій і не паралельна до двох інших.

Площина, перпендикулярна до p ₁, – горизонтально-проекційна.

Площина, перпендикулярна до p ₂, – фронтально-проекційна.

Площина, перпендикулярна до p ₃, – профільно-проекційна.

Всі вище названі площини зображені в таблиці 4.1.

Назва площини вказує на те, до якої площини проекцій дана площина перпендикулярна. У випадку проекційної площини всі точки, криві та прямі лінії, плоскі фігури, які лежатимуть у цій площині, збігатимуться з одним із слідів площини, і саме зі слідом на площині проекцій, до якої ця проекційна площина перпендикулярна. Другий слід завжди буде перпендикулярний до осі проекцій.

Такий збіг сліду площини з усіма елементами, що лежать у ній, називають збираючою властивістю.

Проекційні площини в системі трьох площин проекцій мають три сліди.

Таблиця 4.1 – Проекційні площини

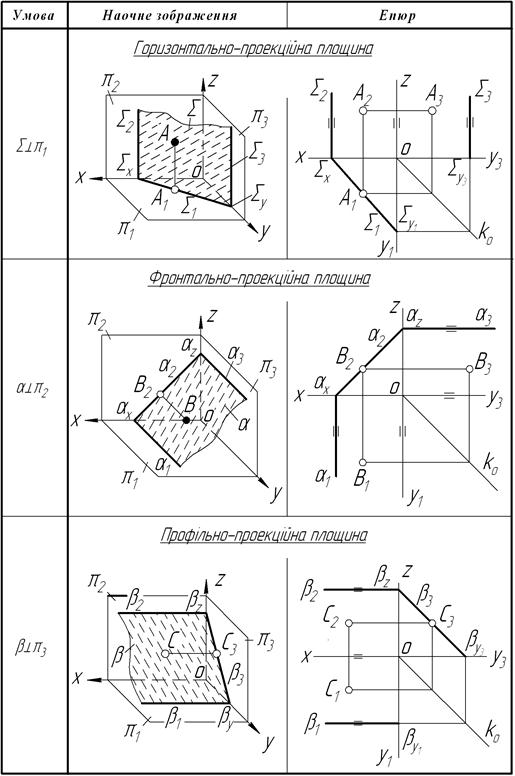На рисунку 4.3 зображена профільно-проекційна осьова площина ─ тобто площина, яка проходить через вісь ОХ. Ця площина може бути бісекторною, якщо вона ділить просторовий кут між p ₁ і p ₂ на дві рівні частини. Така площина характерна тим, що вона є геометричним місцем точок, рівновіддалених від фронтальної ( p ₂) і горизонтальної (p ₁) площин проекцій. Отже, будь-яка точка цієї площини має однакові координати Z і Y. Фронтальний і горизонтальний сліди таких площин збігаються з віссю ОХ.

У системі двох площин проекцій p ₂ і p ₁ осьова площина може задаватися точкою і слідами, які збігаються з віссю ОХ (рис. 4.3).

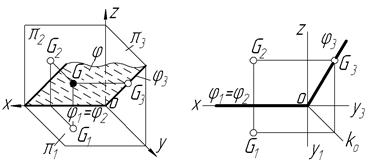
Рисунок 4.3 – Осьова площина

Двічі проекційною (або площиною рівня) називають площину, яка паралельна до однієї із площин проекцій і перпендикулярна до двох інших площин проекцій. Такі площини зображені у таблиці 4.2.

Таблиця 4.2 – Двічі проекційні площини

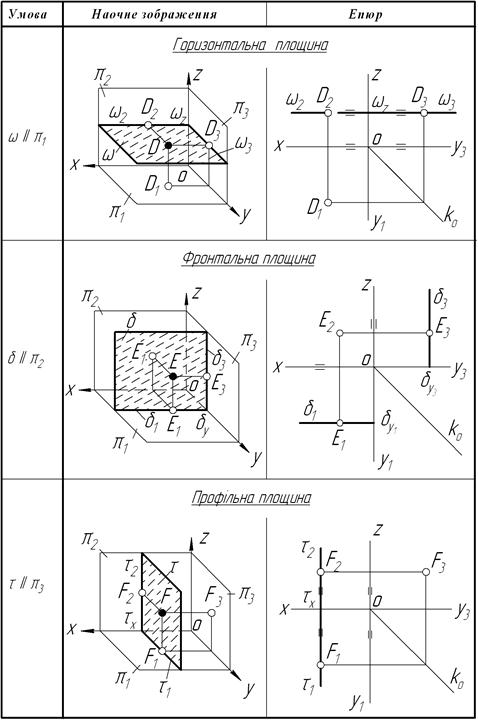Площина, паралельна до p ₁, – горизонтальна.

Площина, паралельна до p ₂, – фронтальна.

Площина, паралельна до p ₃, – профільна.

Назва площини рівня вказує на те, до якої площини проекцій дана площина паралельна. Ці площини мають у системі трьох площин проекцій тільки два сліди, бо до третьої вони паралельні. На площину проекцій, до якої задана площина паралельна, будь-яка множина точок, лінія, плоска фігура, що знаходиться у двічі проекційних площинах, проеціюватимуться в дійсну величину, а на двох інших площинах проекцій проекції цих елементів співпадуть зі слідами площини (за збираючою властивістю проекційної площини).

4.2 Пряма і точка в площині

Пряма може належати площині, бути паралельною до площини і перетинати площину. Точка може належати площині або ж не належати площині.

Розглянемо умови належності прямої і точки до площини:

- Точка належить площині, якщо вона лежить на прямій, яка належить цій площині. На рисунку 4.4а площина a задана двома прямими а і b, що перетинаються в точці А. Точки В і С належать цій площині a також, бо лежать, відповідно, на прямих а і b, що задають площину. Отже, щоб побудувати довільну точку, яка б лежала у площині, необхідно в даній площині провести пряму і на цій прямій вибрати довільну точку.

- Пряма належить площині, якщо вона проходить через дві точки, які належать цій площині. На рисунку 4.4б пряма t, яка з’єднує точки В і С, належить цій площині a. Отже, щоб побудувати пряму, що лежить у площині, необхідно задати дві точки, які належать площині, і через ці точки провести пряму, яка і буде належати даній площині.

- Пряма належить площині,якщо вона проходить через точку, яка лежить у площині і проходить паралельно прямій, що лежить у цій площині. На рисунку 4.4в пряма d, яка проходить через точку В, що належить площині a, є паралельною до прямої в, що лежить у площині a, і буде прямою, яка належить площині a.

	а)
		б)

в)

Рисунок 4.4 – Належність точки та прямої до площини

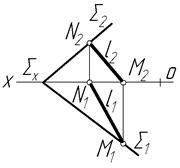У нарисній геометрії правдиве твердження, що пряма належить площині, якщо її сліди лежать на однойменних слідах площини (рис. 4.5).

Рисунок 4.5 – Належність прямої до площини

Отже, щоб провести пряму, яка лежить у даній площині, необхідно задати точку в площині і через цю точку провести пряму, яка паралельна до будь-якої прямої даної площини (в тому числі і одному із слідів даної площини). Якщо точка або пряма лежить у площині особливого положення, то необхідно керуватись збираючою властивістю проекційних площин (підрозділ 4.1) і не проводити попередніх побудов.

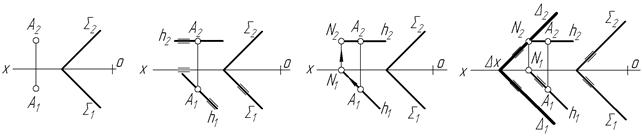
Задача 1. Через відрізок АВ провести горизонтально-проекційну площину S (рис.4.6а).

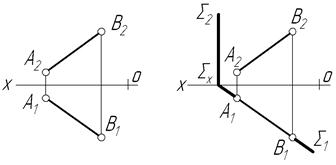Використовуючи збираючу властивість проекційних площин, розуміємо, що горизонтальний слід площини збігається з горизонтальною проекцією прямої АВ. Продовжимо А₁В₁ до перетину з віссю ОХ і знайдемо S_Х ─ точку збігу слідів площини S на осі ОХ, і через неї проведемо фронтальний слід площини S₂, який пройде перпендикулярно до осі ОХ, що властиво всім горизонтально-проекційним площинам. Отже, горизонтально-проекційну площину побудовано і відрізок АВ належить їй (рис. 4.6б).

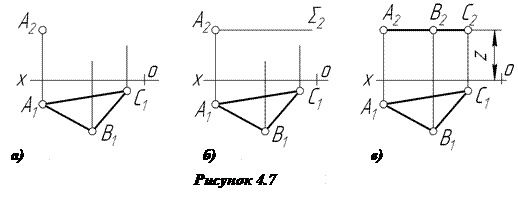
Задача 2. Побудувати відсутні проекції точок, якщо відомо, що точки А, В, С належать горизонтальній площині, заданій трикутником АВС. Визначити відстань площини трикутника АВС до площини проекцій, якій вона паралельна (рис.4.7а).

Відомо з попереднього матеріалу, що горизонтальна площина на площинах проекцій має фронтальний слід, розміщений паралельно до осі ОХ, і що все, що лежить у цій площині, “збирається” фронтальним слідом. Тому через А₂ паралельно до осі ОХ проводимо S₂ ─ фронтальний слід горизонтальної площини (рис. 4.7б). Цей слід “збирає” на себе фронтальні проекції точок В і С. Координата Z і є відстанню від площини S до p₁ (рис.4.7в).

4.3 Головні лінії площини

Серед безконечної множини ліній, які належать площині, заслуговують на увагу так звані головні лінії. Лінії рівня площини або горизонталь, фронталь і профіль, а також лінії найбільшого нахилу відносяться до таких ліній.

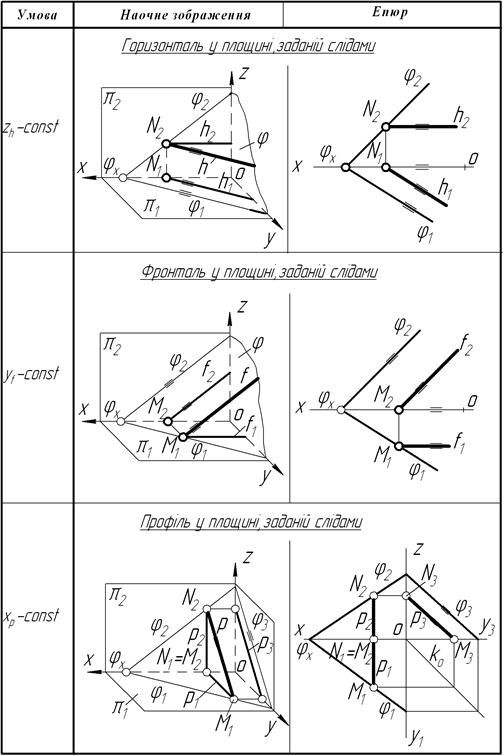
Горизонталь площини – це пряма, паралельна до горизонтальної площини проекцій і лежить у заданій площині (табл. 4.3). Горизонтальний слід для всіх площин, можна розглядати як нульову горизонталь. Координата Z будь-якої точки горизонтального сліду є постійною і дорівнює нулю.

Фронталь площини – це пряма, яка проходить паралельно до фронтальної площини проекцій і лежить у заданій площині (табл. 4.3). Фронтальний слід для всіх площин можна розглядати як нульову фронталь. Координата Y будь-якої точки фронтального сліду є постійною і дорівнює нулю.

Профіль площини – це пряма, яка паралельна до профільної площини проекцій і лежить у заданій площині. Профільний слід для всіх площин можна розглядати як нульовий профіль. Координата Х будь-якої точки профільного сліду є постійною і дорівнює нулю (табл. 4.3).

Таблиця 4.3 – Головні лінії площини

Особливі випадки (табл. 4.4):

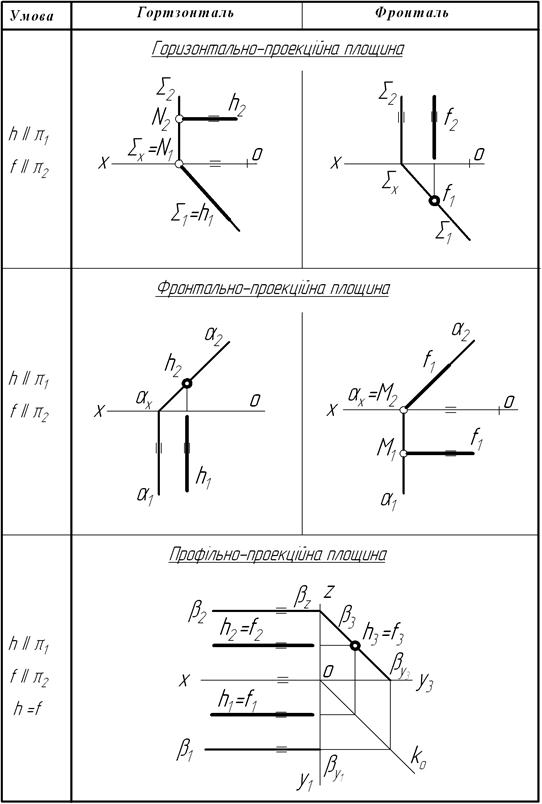
1 Горизонтальна проекція горизонталі горизонтально-проекційної площини t збігається з її горизонтальним слідом (збираюча властивість) t₁ º h₁.

2 Горизонтальна проекція фронталі горизонтально-проекційної площини t збігається з її горизонтальним слідом і вироджується в точку.

3 Фронтальна проекція горизонталі фронтально-проекційної площини d виродиться в точку, яка збігатиметься з фронтальним слідом площини.

4 Фронтальна проекція фронталі фронтально-проекційної площини d збігається з її фронтальним слідом d ₂ º f₂.

5 Для профільно-проекційної площини як фронталь, так і горизонталь вироджується у профільно-проекційну пряму. Профільні проекції горизонталі і фронталі лежать на профільному сліді площини a і проеціюютьсяються в точку h₃ º a₃. У профільно-проекційній площині горизонталь одночасно є і фронталлю.

Таблиця 4.4 – Горизонталь і фронталь в проекційних площинах

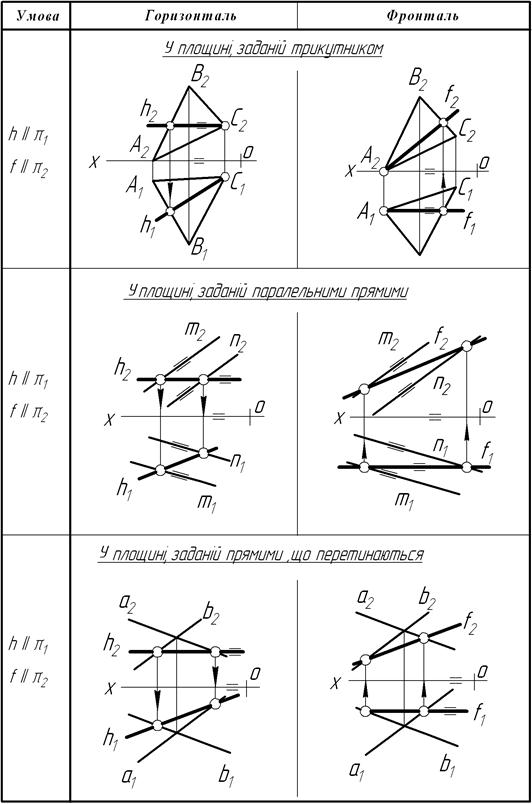
У таблиці 4.5 показано побудову горизонталі та фронталі у площинах загального положення, які задані не слідами, а трикутником, паралельними та перетинними прямими.

Таблиця 4.5 – Горизонталь і фронталь у площинах загального положення заданих не слідами

До головних ліній площини належить і лінія найбільшого нахилу.

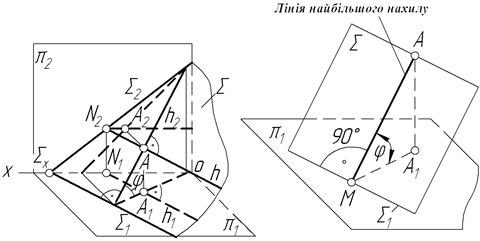
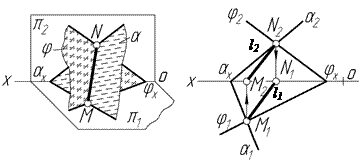
Лінія найбільшого нахилу – це лінія, яка лежить у заданій площині і проходить перпендикулярно до горизонталі площини (лінія найбільшого нахилу до p₁) або перпендикулярно до фронталі площини (лінія найбільшого нахилу до p₂), або перпендикулярно до профілю площини (лінія найбільшого нахилу до p₃). Побудова лінії найбільшого нахилу до p₁ показана на рисунку 4.8. Через будь-яку точку К, вибрану на горизонталі площини h, проводимо пряму MN, яка належить площині S і перпендикулярна до h. Ця лінія і буде лінією найбільшого нахилу площини S до площини проекцій p₁.

		Рисунок 4.8 – Лінія найбільшого нахилу

Прямий кут між МN і h спроеціюється на p₁ без спотворення, бо одна із сторін цього прямого кута є горизонтальною прямою. Таким чином, горизонтальна проекція лінії найбільшого нахилу площини j перпендикулярна до горизонтальної проекції горизонталі, а отже, і до горизонтального сліду площини: М₁N₁ ^ h₁; М₁N₁ ^ S₁. Кут j між лінією найбільшого нахилу і горизонтальною площиною проекцій дорівнює куту нахилу площини S до горизонтальної площини проекцій. Кут j - це кут між лінією найбільшого нахилу і її горизонтальною проекцією.

Задача 2. Знайти дійсну величину кута нахилу площини j до горизонтальної площини проекцій - p₁ (рис.4.9а).

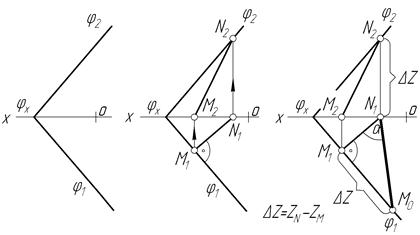Щоб розв’язати дану задачу (рис.4.9б), в площині j потрібно побудувати одну з ліній найбільшого нахилу до горизонтальної площини проекцій. Для цього будуємо її горизонтальну проекцію ─ N₁M₁ ^ j₁. Далі добудовуємо фронтальну проекцію лінії найбільшого нахилу із умови належності цієї лінії до площини (сліди прямої лежать на слідах площини). Кут a - це кут нахилу площини j до площини p₁. Дійсну величину кута a знаходимо способом прямокутного трикутника – кут між дійсною величиною і проекцією лінії найбільшого нахилу до p₁.

	а)

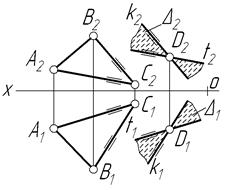
Задача 3. Побудувати фронтальну проекцію трикутника АВС, який належить площині a.

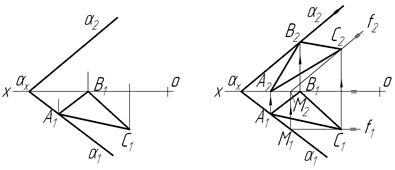З графічної умови задачі (рис.4.10а) бачимо, що задано горизонтальну проекцію трикутника АВС. Всі вершини трикутника належать площині a, а отже, кожна з них лежить на прямій, яка належить a. Сліди площини – це дві прямі, що перетинаються і належать площинам проекцій p₁ і p₂. Використавши це положення, знайдемо фронтальні проекції точок А і В. Для знаходження фронтальної проекції С₂ скористаємося фронталлю площини a, яку проведемо через С₁. Фронтальна проекція С₂ лежатиме на фронтальній проекції фронталі по лінії проекційного зв’язку, проведеній через С₁. З’єднаємо знайдені А₂, В₂, С₂ – одержимо шукану фронтальну проекцію.

	Рисунок 4.10

4.4 Взаємне положення двох площин

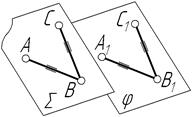Дві площини у просторі можуть бути паралельними або перетинними. У першому випадку вони не мають спільних точок, у другому спільними точками цих площин є лінія їх перетину (пряма, спільна для обох площин).

Рисунок 4.11 – Паралельні площини в просторі

Розглянемо випадок взаємної паралельності площин. Для цього скористаємося відомими положеннями про те, що дві площини паралельні тоді, коли перетинні прямі однієї площини відповідно паралельні двом перетинним прямим другої площини (рис.4.11). У площині S дві прямі АВ і ВС перетинаються і паралельні відповідно А₁В₁ і В₁С₁ двом перетинним прямим площини j.

На рисунках 4.12, 4.13 також зображені дві паралельні площини a і b, які задані слідами.

		l1
	Рисунок 4.12 – Паралельні площини на наглядному зображені		Рисунок 4.13 – Паралельні площини на епюрі

Напрошується висновок 1: якщо площини паралельні, то їх однойменні сліди також паралельні. Справедливим буде і обернене твердження (рис.4.13).

Виходячи з того, що сліди площини є нульовими горизонталями, фронталями і профілями, справедливий також висновок 2: у паралельних площинах горизонталі, фронталі і профілі однієї площини паралельні відповідно до горизонталей, фронталей і профілей другої площини.

Рисунок 4.14 – Перетинні площини

Слід зауважити, що для площин довільного положення, заданих слідами, достатньо лише паралельності двох слідів на епюрі, щоб стверджувати – ці площини паралельні. Але, якщо це дві площини особливого положення (зокрема профільно-проеціююючі), то судити про паралельність площин за двома парами слідів не можна (рис. 4.14). Обов’язково треба побудувати сліди площини на третій площині проекцій, до якої задані дві площини перпендикулярні, і тільки тоді можна стверджувати чи паралельні площини: якщо S₃ ║ Δ₃ ─ то вони паралельні; якщо S₃´Δ₃ ─ то вони перетинаються.

Отже, якщо хоч одна пара однойменних слідів двох площин перетинаються, то і ці площини перетинаються.

Задача 1. Побудувати площину через точку А паралельно до площини S (площину задати слідами). Графічна умова задачі зображена на рисунку 4.15а.

Через точку А проводимо горизонталь площини Δ (яку треба побудувати). h₂ ║ ОХ, а h₁ ║S ₁. Знаходимо фронтальний слід побудованої горизонталі N (N₂;N₁). Через фронтальний слід горизонталі N º N₂ проводимо фронтальний слід Δ₂ площини Δ. Δ₂ ║ S₂ через N₂. Знаходимо точку сходу слідів Δ_Х. Δ₂´ ОХ= Δ_Х. Будуємо горизонтальний слід площини Δ. Δ₁ ║ S₁ (висновок1). Отже площини Δ і S - паралельні.

	а)		б)
			в)		г)
			Рисунок 4.15

Задача 2. Через точку D побудувати площину, паралельну до площини трикутника АВС.

Рисунок 4.16

Скористаємося положенням: якщо дві прямі, що перетинаються, однієї площини, паралельні двом перетинним прямим другої площини, то такі площини паралельні. Проведемо через точку D дві прямі паралельно до двох сторін трикутника і одержимо площину, паралельну до трикутника (рис. 4.16).

Розглянемо перетинні площини. Дві площини перетинаються по прямій лінії, для побудови якої досить визначити дві точки, що одночасно належать обом площинам, або одну таку точку і напрямок прямої перетину.

Якщо площини задані слідами, то лінія перетину визначається точками перетину однойменних слідів площин.

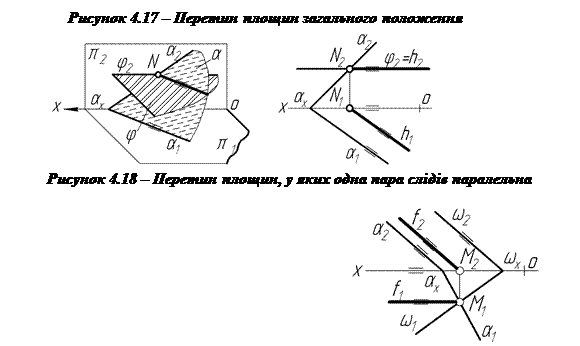
На рисунку 4.17 задано площини Δ і a, однойменні сліди яких перетинаються в точках M i N. Очевидно, що ці точки будуть спільними для обох площин, тобто пряма MN (l) буде лінією перетину заданих площин. Для побудови проекцій лінії перетину l визначаємо проекції точок M i N і сполучаємо їх одноіменні проекції. Отже, пряма l (l₂, l₁) є лінією перетину площин Δ і a. Залежно від розміщення слідів двох площин, що перетинаються, можливі різні способи побудови ліній їх перетину на епюрі:

1) дві площини, однойменні сліди яких перетинаються в межах формату ─ лінію перетину відображають без особливих додаткових побудов (рис.4.17);

2) дві площини, у яких тільки одна пара слідів перетинається в межах формату, а друга не перетинається (паралельні) (рис.4.18);

3) однойменні сліди двох площин не перетинаються в межах формату (рис. 4.20).

Задача 3. Побудувати лінію перетину двох площин a і w (рис.4.19).

Рисунок 4.19

Згідно з умовою фронтальні сліди заданих площин паралельні, а отже, фронтальна проекція лінії перетину буде проходити паралельно a₂ і w₂ з точки перетину горизонтальних слідів – М₂. Ця лінія буде слугувати для заданих площин фронталлю.

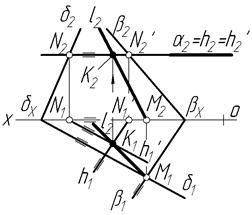Задача 4. Побудувати лінію перетину двох площин d і b (рис.4.20).

Рисунок 4.20

У даній задачі легко знаходиться одна точка лінії перетину. Вона лежить на перетині горизонтальних слідів площини М(М₁;М₂). Друга пара слідів перетинається за межами формату, тому треба знайти напрямок лінії перетину, тобто знайти іншу, довільну точку прямої перетину, спільну для обох площин. Скористаємося методом допоміжних січних площин-посередників. Обираємо площину-посередник, розташовану в просторі так, щоб ця допоміжна площина перетинала обидві задані площини по лініях, які легко будуються – горизонталях або фронталях.

У даному випадку вибираємо горизонтальну площину a, яка перетинає задані площини d і b по горизонталях h(h₂;h₁) i h¢(h₂¢; h₁¢). На перетині цих горизонталей дістанемо спільну для заданих площин допоміжну точку К(К₁;К₂) - h₁ і h₁¢ перетинаються в К₁. На лінії проекційного зв’язку на h₂₌h₂¢ знаходимо К₂.

З’єднавши К₂ з М₂ і К₁ з М_{1 ,} знайдемо шукану лінію перетину двох площин d і b.

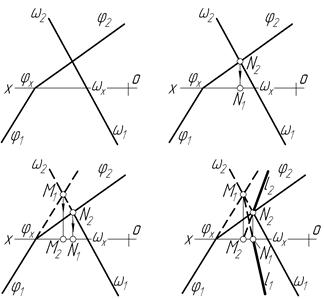
Задача 5. Побудувати лінію перетину двох площин a і w, які задано на рисунку 4.21.

План розв’язку задачі:

1.

а)

б)

Знайти точку перетину фронтальних слідів площин a і w (рис.4.21б).

2. Знайти точку перетину горизонтальних слідів площин a і w (перетин їх у другій чверті) (рис. 4.21в).

3. Побудувати лінію перетину двох площин, з’єднавши M₂ і N₂ та M₁ і N₁ з урахуванням видимості прямої (рис.4.21г).

4.5 Взаємне положення прямої і площини

Пряма і площина можуть займати одна відносно одної такі положення:

а) пряма належить площині;

б) пряма паралельна площині;

в) пряма перетинає площину.

Належність прямої до площини вже описана в підрозділі 4.2.

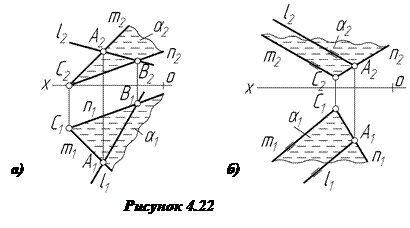
Задача 1. Побудувати проекції довільної прямої l в площині a, яка задана двома перетинними прямими m i n (рис.4.22).

Скористаємось основною аксіомою належності, яка твердить, що пряма належить площині, якщо дві точки цієї прямої належать цій же площині. На заданих прямих m i n вибираємо довільні точки А і В. Ці точки і визначають шукану пряму l (l₁;l₂). Якщо одна із точок А або В буде невласною, тоді аксіома належності формулюється так: пряма належить площині, якщо має з площиною одну спільну точку і паралельна будь-якій прямій, яка розташована (лежить) у цій площині. На рисунку 4.22б показано проекції прямої l, яка належить площині a. Ця пряма перетинає пряму n в точці А і паралельна до прямої m.

Пряма паралельна до площини, коли вона (пряма) паралельна будь-якій прямій, яка лежить у цій площині.

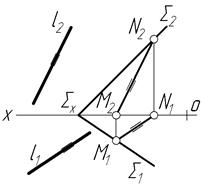На рисунку 4.23 пряма l паралельна площині S, l₁ ║ N₁M₁; l₂ ║ N₂M₂; - бо вона паралельна до прямої MN, яка лежить у площині S. Належність прямої MN до площини підтверджує те, що сліди прямої лежать на слідах площини.

Дата добавления: 2014-12-16