ПЛОЩИНА 2 страница

Рисунок 4.23

На рисунку 4.24 пряма t паралельна до площини, яка задана трикутником АВС, бо пряма t паралельна до прямої АS, яка належить трикутнику АВС (t₁ ║ А₁S₁; t₂ ║ А₂S₂). Ця задача має багато розв’язків. Наприклад, пряму t можна провести паралельно до будь-якої сторони трикутника АВС і вона також буде паралельною до площини трикутника.

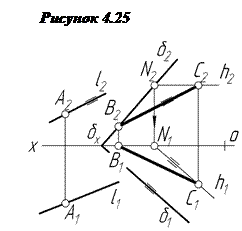
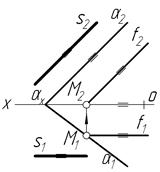На рисунку 4.25 пряма S паралельна площині a, бо вона (пряма) паралельна до однієї із прямих особливого положення в площині (в даному випадку до фронталі f) (s₁║f₁;s₂║f₂), а також до фронтального сліду a₂ цієї площини.

		Рисунок 4.24

Рисунок 4.26

Для того, щоб перевірити чи паралельна пряма l до площини d (рис. 4.26), достатньо побудувати проекції прямої лінії, яка належить площині і перевірити чи паралельні між собою однойменні проекції прямої l і прямої, що належить площині. Для цього в площині d беремо довільну точку С (яка лежить на горизонталі площини h) і через С₂ проводимо С₂В₂ ║ l₂. Із умови належності прямої СВ до площини d будуємо В₁С₁. Бачимо, що В₁С₁ не паралельна l₁.

Отже, пряма l не паралельна до площини d.

Задача 2. Через задану точку провести площину паралельно до заданої прямої (рис. 4.27).

Рисунок 4.27

Зрозуміло, що в цьому випадку через деяку точку А, можна провести пучок площин (a, b,...) віссю яких є пряма t, що проходить через точку А паралельно до прямої l (рис.4.27). Щоб мати єдиний розв’язок, треба задати будь-яку додаткову умову. У даному випадку нехай це буде точка сходу слідів a_Х.

Проводимо через точку А пряму t паралельно до прямої l. Пряма t є віссю пучка площин, які можна провести через точку А паралельно до прямої l (рис.4.28). Одну з цих площин, а саме шукану a, можна провести виходячи з того, що сліди такої площини повинні пройти через однойменні сліди прямої t. Тому знаходимо сліди прямої t M=M₁ i N=N₂. Через ці точки і точку сходу слідів, яка задана, проводимо сліди площини a₂ і a₁. Площина a проходить через точку А і паралельна до прямої l.

	Рисунок 4.28

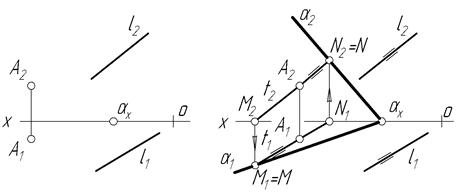
Пряма перетинає площину тоді, коли вона не належить площині і не паралельна їй, а перетинає її в певній точці. Якщо пряма загального положення перетинається з площиною особливого положення, то точка перетину знаходиться без додаткової побудови.

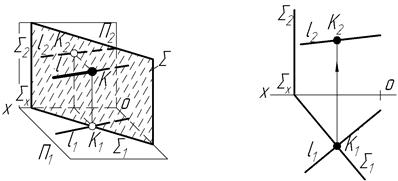На рисунку 4.29 зображена пряма l і горизонтально-проекційна площина S. Точка К належить і прямій l і площині S. Горизонтальна проекція К₁ буде обов’язково лежати на горизонтальному сліді S₁ проекційної площини.

	Рисунок 4.29

Для побудови точки перетину прямої з площиною загального положення S треба виконати такі побудови (рис.4.30):

1) через задану пряму АВ провести допоміжну площину a (особливого положення);

2) побудувати лінію перетину MN заданої площини j з допоміжною a;

3) зробити висновок про положення прямих MN і АВ.

Такий висновок необхідно зробити тому, що пряма MN спільна для площин j і a, а пряма АВ лежить тільки в площині a. Як результат зробленого аналізу можна виділити такі випадки:

а) прямі MN і АВ не мають спільних точок – пряма АВ паралельна до площини j;

б) прямі MN і АВ збігаються ─ пряма АВ лежить у площині j;

в) прямі MN і АВ перетинаються ─пряма АВ перетинає площину j в точці К.

На рисунку 4.30 задано площину j (довільного положення) і пряму АВ, яка перетинає цю площину. Через пряму АВ проводимо допоміжну горизонтально-проекційну площину a; лінія MN – це лінія перетину двох площин j і a. Точка К, яка є точкою перетину прямих MN і АВ, – шукана точка перетину прямої АВ з площиною j.

Розглянутий план розв’язку є загальним для всіх випадків задання площини.

Задача 3. Побудувати точку перетину прямої l з площиною, яка задана двома паралельними прямими m i n. Площину вважати непрозорою (рис.4.31а).

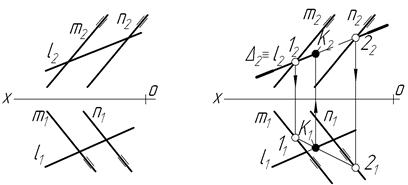Через пряму l (рис. 4 31б) проводимо фронтально-проекційну площину Δ. Зображено тільки її фронтальний слід Δ₂ (горизонтальний слід Δ₁ у побудові участі не бере). Побудовано лінію 12 перетину площини Δ із заданою площиною. На перетині 12 і АВ одержимо шукану точку К. Методом конкуруючих точок, описаним у підрозділі 3.7, знаходимо видимість прямої відносно площини.

	а)

Задача 4. Побудувати перетин прямої l з площиною, що задана двома перетинними прямими (рис.4.32а).

У даному випадку пряма l особливого положення – фронтально-проекційна.

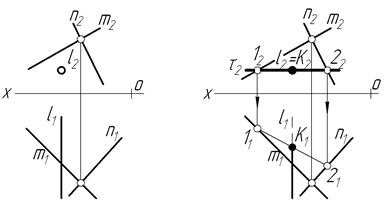У зв’язку з цим, відразу відомо, що l ₂º К₂ – фронтальна проекція прямої збігається з фронтальною проекцією лінії перетину (збираюча властивість) (рис.4.32б). Тому проводимо допоміжну горизонтальну площину t через l₂. Знаходимо лінію перетину допоміжної площини t із заданою площиною ─ це пряма 12(1₂2₂;1₁2₁). Знаходимо точку перетину К, вірніше, її горизонтальну проекцію ─ К₁. Фронтальна проекція К₂ лежить на t₂ і збігається з l₂.

	а)

Задача 5. Побудувати перетин прямої l з площиною, заданою трикутником, і визначити видимість прямої відносно площини трикутника. Площину АВС вважати непрозорою (рис.4.33а).

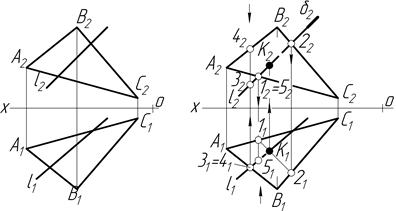За аналогією розв’язку попередніх задач знаходимо точку К (рис.4.33б). Видимість визначаємо за допомогою методу конкуруючих точок 1-2 і М-3, який описаний детально в підрозділі 4.7.

	а)

Розглянувши спосіб знаходження точки перетину прямої з площиною, можна перейти до побудови лінії перетину плоских фігур, якщо одна із них задана не слідами, або обидві площини задані не слідами. Зрозуміло, що можна було б попередньо побудувати сліди таких площин, а потім визначити лінію їх перетину, користуючись викладеними раніше міркуваннями і способами. Однак, у цих випадках побудова лінії перетину двох площин цілком можлива без знаходження слідів площини. Слід зазначити, що в таких задачах можна знайти лінію перетину, використавуючи метод посередників, однак цей метод ускладнює побудову.

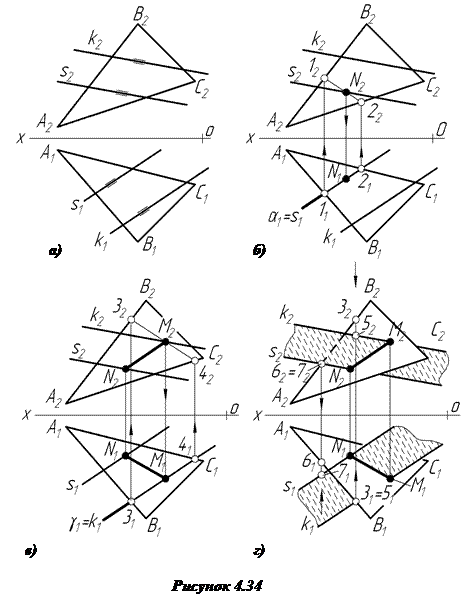
Задача 6. Побудувати лінію перетину трикутника АВС з площиною, заданою двома паралельними прямими k i s (рис.4.34).

Побудова лінії перетину MN у цій задачі зводиться до знаходження точок M i N, які є точками перетину прямих k i s з площиною трикутника АВС, і побудови через ці точки відрізка прямої лінії, що буде лінією перетину двох площин. Точку N знайдемо як точку перетину прямої s з площиною трикутника АВС (рис. 4.34б). Для цього через пряму s проведемо допоміжну горизонтально-проекційну площину a. Площина a перетинає трикутник АВС по прямій 12(1₁2₁;1₂2₂). На фронтальній проекції знаходимо N₂, як результат перетину s₂ з 1₂2₂. По лінії проекційного зв’язку на s₁ знаходимо N₁. Отже, знайдемо точку N(N₂;N₁).

Аналогічно знаходимо точку M(M₂;M₁) (рис.4.34в). Точка М – це точка перетину прямої k з площиною трикутника АВС. Для цього через пряму k проводимо допоміжну площину g. Площина g перетинає трикутник АВС по лінії 34(3₁4₁;3₂4₂). На перетині k₂ з 3₂4₂ знаходимо М₂. За лінією проекційного зв’язку на k₁ знайдемо M₁ , з’єднуємо точки N і М і дістанемо шукану лінію перетину заданих площин. Вважаючи площини непрозорими, визначаємо видимість першої відносно другої за допомогою конкуруючої пари точок 3-5; 6-7 (рис. 4.34г).

Побудова лінії перетину двох площин значно спрощується, якщо одна із площин є проекційною.

4.6 Пряма, перпендикулярна до площини, і взаємно перпендикулярні прямі і площини

Пряму, перпендикулярну до площини, слід розглядати як окремий випадок прямої, яка перетинає площину під прямим кутом.

З курсу елементарної геометрії відомо, що пряма перпендикулярна до площини, якщо вона перпендикулярна до двох перетинних прямих, які лежать у даній площині (рис.4.35а).

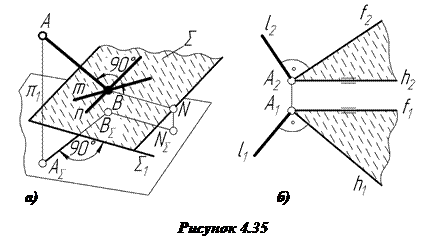На основі властивостей проеціювання прямого плоского кута можна зробити висновок, що проекції перпендикуляра до площини будуть розміщені таким чином:

1) горизонтальна проекція ─ під прямим кутом до горизонтальної проекції горизонталі і до горизонтального сліду площини (рис.4.35б) ;

2) фронтальна проекція ─ під прямим кутом до фронтальної проекції фронталі і до фронтального сліду площини (рис.4.35б);

3) профільна проекція ─ під прямим кутом до профільної проекції профільної прямої і до профільного сліду площини.

Справедливе і обернене твердження, а тому, якщо площина перпендикулярна до прямої, то горизонтальний слід площини або горизонтальна проекція горизонталі перпендикулярна до горизонтальної проекції прямої, а фронтальний слід і фронтальна проекція фронталі площини перпендикулярні до фронтальної проекції прямої.

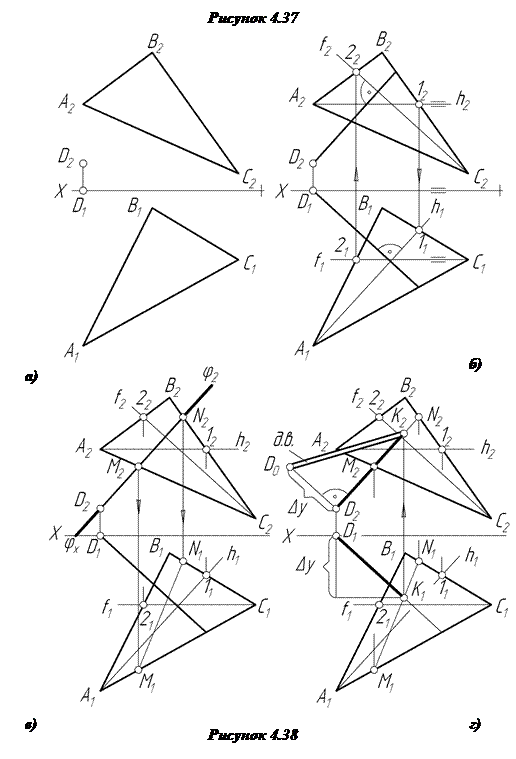
Задача 1. Визначити відстань від точки А до площини S (рис.4.36).

Найкоротша відстань від точки А до площини вимірюється перпендикуляром. На підставі викладеного вище, проекції перпендикуляра пройдуть через точку А перпендикулярно слідам площини. Основою перпендикуляра – точкою перетину перпендикуляра з площиною – є точка К. Її горизонтальну проекцію К₁ знаходимо за збираючою властивістю проекційної площини, а К₂ ─ по лінії проекційного зв’язку на фронтальній проекції перпендикуляра А₂К₂. А₁К₁ – дійсна величина відстані від точки А до площини S, бо фронтальна проекція А₂К₂ розміщена паралельно до горизонтальної площини проекцій (АК - горизонтальний відрізок).

	Рисунок 4.36

Задача 2. Знайти дійсну величину відстані від точки А до площини S.

Відомо, що відстань від точки до площини вимірюється відрізком перпендикуляра від заданої точки до основи перпендикуляра – точки перетину перпендикуляра з площиною. Для цього з точки А проводимо перпендикуляр (рис. 4.37) до площини. Фронтальна проекція пройде через А₂ перпендикулярно до S₂, горизонтальна проекція ─ через А₁ перпендикулярно до S_{1 .} Основу перпендикуляра, точку К, знаходимо як точку перетину прямої (перпендикуляра) з площиною. Спосіб описано в задачах на рисунках 4.30; 4.31; 4.32. Знайшовши відстань у проекціях А₂К₂ і А₁К₁, знаходимо дійсну величину АК, використовуючи правило прямокутного трикутника. А₀К₁ – дійсна величина відстані від точки А до площини S.

Задача 3. Знайти дійсну величину відстані від точки D до трикутника АВС (рис. 4.38).

Для того, щоб провести проекції перпендикуляра, у трикутнику АВС будуємо насамперед горизонталь h через вершину А і фронталь f через вершину С. Потім з проекцій точки D проводимо проекції перпендикуляра: з точки D₁ ─ перпендикулярно до h₁ і із точки D₂ ─ перпендикулярно до f ₂ (рис. 4.38б). Далі через перпендикуляр проводимо допоміжну фронтально-проекційну площину j. Будуємо лінію перетину заданої площини трикутника АВ С з допоміжною площиною j - це буде лінія MN(M₂N₂;M₁N₁). І, нарешті, знаходимо основу перпендикуляра - точку К(К₂,К₁). Відстань від точки D до трикутника АВС знайдено в проекціях D₂K₂ і D₁K₁. Дійсну величину D₀K₂ знаходимо, застосовуючи правило прямокутного трикутника (4.38г).

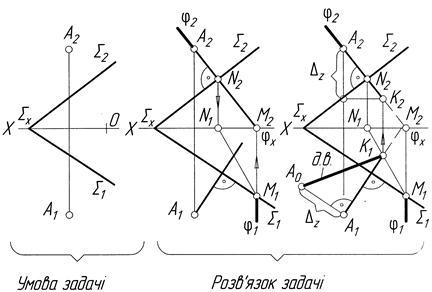
Задача 4. З точки А, що належить площині S, встановити перпендикуляр довжиною 35 мм (рис.4.39).

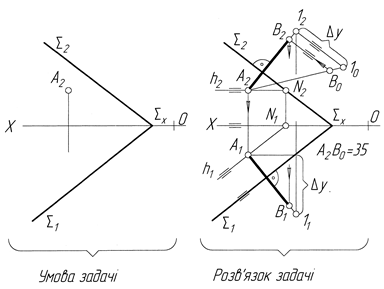Точка А, яка належить площині S, задана своєю фронтальною проекцією. Знаходимо її горизонтальну проекцію за допомогою горизонталі h. Далі з точки А(А₂,А₁) проводимо проекції перпендикуляра: через А₂ перпендикулярно до S₂, а через А₁ перпендикулярно до S₁. Обмежуємо цей перпендикуляр довільною точкою 1(1₂,1₁). Методом прямокутного трикутника знаходимо дійсну величину обмеженої частини перпендикуляра А₂1₀. На дійсній величині від точки А₂ відкладаємо 35 мм. Одержимо точку В₀. З побудови на рисунку 4.39 видно, як будувалися проекції В₂ і В₁ (показано стрілками). Отже, А₂В₂ і А₁В₁ – проекції перпендикуляра, який проведено з площини S, дійсна величина його дорівнює 35 мм.

	Рисунок 4.39

Взаємноперпендикулярні площини – це окремий випадок двох площин, які перетинаються під прямим кутом. Для побудови зображення таких площин на епюрі скористаємось твердженням зі шкільного курсу геометрії про те, що дві площини взаємно-перпендикулярні тоді, коли:

1) одна проведена через перпендикуляр до іншої;

2) одна перпендикулярна до будь-якої прямої, що лежить у другій площині.

Отже, побудова площини, перпендикулярної до заданої, зводиться до проведення спочатку перпендикуляра до однієї з цих площин, а потім – до побудови площини через цей перпендикуляр або проведення в одній із площин прямої лінії й побудови другої площини, перпендикулярної до цієї прямої.

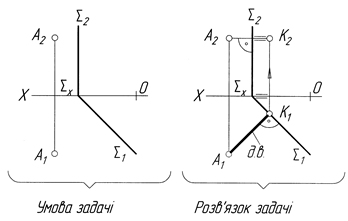
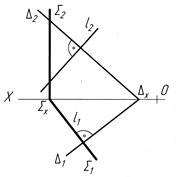
Задача 5. Побудувати площину Σ, перпендикулярну до заданої площини Δ (рис.4.40).

Будуємо перпендикуляр l до площини Δ. Для цього проводимо l₁ ^ Δ₁ і l₂ ^ Δ₂ Через перпендикуляр l проводимо площину Σ (у даному випадку горизонтально-проекційну). Оскільки через перпендикуляр l можна провести безліч площин, то шукана площина Σ є однією з них.

	Рисунок 4.40		Рисунок 4.41

Задача 6. Побудувати площину a, перпендикулярну до площини j (рис.4.41).

У заданій площині j будуємо довільну пряму l, перпендикулярно до якої проводимо площину a - одну із безлічі можливих. Площини a і j взаємно перпендикулярні. Наведені приклади підтверджують положення, що в обох випадках задачі мають безліч розв’язків. Тому, щоб дістати єдиний розв’язок, потрібна додаткова умова.

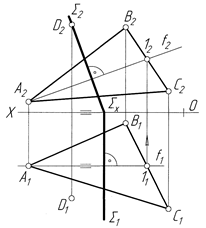Задача 7. Через задану точку D провести фронтально-проекційну площину S, перпендикулярно до площини трикутника АВС (рис.4.42).

Рисунок 4.42

Додатковою умовою в цій задачі є перпендикулярність шуканої площини до площини трикутника АВС і фронтальної площини проекцій. Тому спочатку у заданій площині проводимо фронталь f(f₁;f₂), до якої будуємо перпендикулярну площину S: S₂ ^ f₂ i, очевидно, S₁ ^ f₁. Таким чином, площина S перпендикулярна до заданої, бо вона перпендикулярна до однієї з її фронталей, і проходить через точку D.

Якщо йдеться про зображення на епюрі двох взаємно перпендикулярних площин, слід мати на увазі, що:

1) 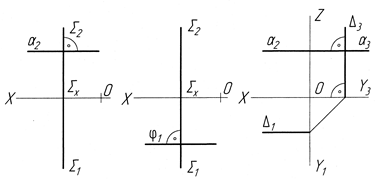однойменні сліди двічі проекційних площин взаємно-перпендикулярні на тій площині проекцій, до якої обидві задані площини перпендикулярні (рис.4.43);

	Рисунок 4.43

2) 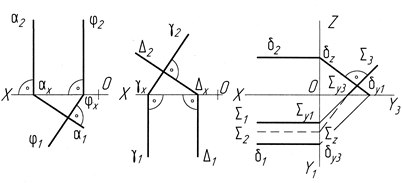однойменні сліди проекційних площин взаємно перпендикулярні лише на тій площині проекцій, до якої обидві задані площини перпендикулярні, інші сліди – ні (рис.4.44);

	Рисунок 4.44

3) якщо дві площини довільного положення на епюрі мають перпендикулярні однойменні сліди, то це ще не є ознакою перпендикулярності цих площин.

Дві перетинні прямі, кут між якими дорівнює 90°, це – взаємно перпендикулярні прямі. Розглянемо питання про побудову зображення двох перпендикулярних прямих. Для цього користуються відомими положеннями про те, що дві прямі перпендикулярні одна до одної тільки тоді, коли через одну з них можна провести площину, перпендикулярну до іншої.

Рисунок 4.45

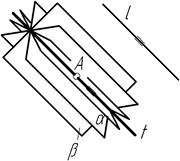
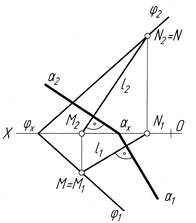
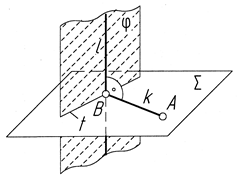Тому, щоб побудувати пряму k перпендикулярно до заданої прямої l, (рис.4.45). треба взяти довільну точку А поза прямою l і через цю точку провести допоміжну площину S, перпендикулярну до прямої l. Потім слід побудувати точку В перетину прямої l з площиною S за допомогою лінії перетину t площини S і допоміжної площини j. Сполучивши точки В і А, дістанемо шукану пряму k, перпендикулярну до заданої прямої l.

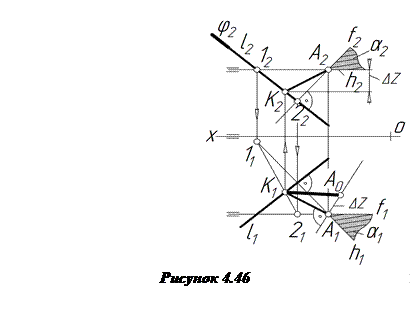
Задача 8. Визначити відстань від заданої точки А до прямої загального положення l (рис.4.46).

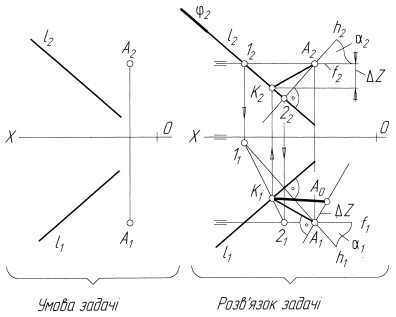Відстань від точки до прямої вимірюється відрізком перпендикуляра, опущеного з точки на пряму. Для побудови через точку А проводимо допоміжну, перпендикулярну до прямої l, площину a. Задаємо її двома прямими, що перетинаються в точці А, а саме горизонталлю і фронталлю. Оскільки площина має бути перпендикулярною до прямої l, то h₁ ^ l₁, а f₂ ^ l₂. Далі знаходимо точку К(К₂К₁) – точку перетину l з площиною a. Для цього через пряму l проводимо допоміжну фронтально-проекційну площину j. Знаходимо лінію перетину 12(1₂2₂;1₁2₁) площини a з площиною j. На перетині 1₁2₁ з l знаходимо К₁ по лінії проекційного зв’язку на l₂ знаходимо К₂. АК(А₂К₂;А₁К₁) – відстань від точки А до прямої l. А₀К₁ - дійсна величина відстані, знайдена методом прямокутного трикутника.

При розв’язуванні задач часто треба будувати проекції кута між прямою й площиною і кута між двома площинами. Зазначимо, що розв’язування таких задач повністю грунтується на наведених відомостях про взаємне положення двох площин, прямої й площини. Ці задачі можна розв’язати, користуючись викладеними вище міркуваннями і способами класичної нарисної геометрії, однак, для розв’язку цих задач можна скористатись способами, які будуть викладені в наступному розділі. За допомогою способів перетворення епюра розв’язок і побудова значно спрощується.

Питання та завдання для самоперевірки

1 Якими елементами може задаватися площина?

2 Як називається площина, розташована перпендикулярно:

a) до горизонтальної площини проекції; б) до фронтальної площини проекції?

3 Як називається площина, розташована паралельно:

a) до горизонтальної площини проекції; б) до фронтальної площини проекції?

4 Яку пряму називають горизонталлю площини; фронталлю площини?

5 Як проходить горизонтальна проекція горизонталі; фронтальна проекція горизонталі?

6 Як проходить горизонтальна проекція фронталі; фронтальна проекція фронталі?

7 Яку пряму називають лінією найбільшого нахилу площини до горизонтальної площини проекції; до фронтальної площини проекції?

8 Яке взаємне положення можуть займати пряма й площина; дві площини?

9 Чим визначається взаємна паралельність двох площин?

10 У чому суть загального способу побудови лінії перетину двох площин?

11 Яка ознака паралельності прямої й площини?

12 Яка послідовність побудов для знаходження точки перетинупрямої з площиною?Як визначити “видимість” прямої у цьому разі?

13 Яка ознака перпендикулярності прямої й площини? Як на епюрі розміщуються проекції перпендикуляра до заданої площини?

14 На чому грунтується побудова двох взаємно перпендикулярних площин і які гра­фічні операції треба виконати для цього?

15 Як будують на епюрі дві взаємно-перпендикулярні прямі довільного положення?

16 Побудуйте довільний паралелограм, площина якого була б паралельна до площини довільного положення, заданої горизонтальним і фронтальним слідами.

17 Побудуйте лінію перетину двох площин довільного положення, горизонтальні та фронтальні сліди яких перетинаються в одній точці на осі ОХ.

18 Побудуйте точку перетину довільної прямої з профільно-проекційною площиною.

19 Побудуйте точку перетину довільної прямої з довільним трикутником.

20 Задайте дві довільні площини:

а) парою паралельних прямих; б) парою перетинних прямих.

21 Побудуйте лінію перетину цих площин, не визначаючи їх слідів.

22 Побудуйте лінію перетину двох довільних фігур — паралелограма і трикутника. Виділіть різними кольорами видимі їх частини.

23 Задайте довільну площину парою перетинних прямих і у точці перетину прямих поставте до площини перпендикуляр довжиною 50мм, не будуючи слідів площини.

24 Задані довільна площина Р і довільний відрізок АВ поза нею. Через відрізок АВ проведіть площину Q, перпендикулярну до площини Р.

Дата добавления: 2014-12-16