Динамика 2 страница

7. Произвести вычисления

N _ср = 0,8 МВт.

№ 12. На краю диска, масса которого m и радиус R, стоит человек массой M. Диск совершает вращательное движение с частотой n об/с. Чему равна кинетическая энергия системы? Чему равна работа внешних сил, в результате действия которых частота вращения увеличивается вдвое?

Р е ш е н и е.

Записать формулу кинетической энергии вращающегося тела

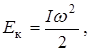(1)

где I - момент инерции системы; w - угловая скорость вращения системы.

Выразить момент инерции системы I и угловую скорость w. Момент инерции системы складывается из моментов инерции тел системы

I = I ₁ + I ₂,

где I ₁ = 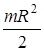- момент инерции диска; I ₂ = 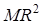- момент инерции человека. Угловая скорость w = 2p n. Подставить выражения I ₁ и I ₂ в формулу (1)

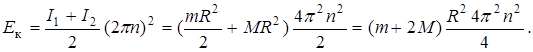
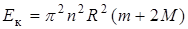. (2)

Работу сил определить по теореме об изменении кинетической энергии

.

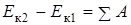Используя уравнение (2) и условие n ₂ = 2 n ₁, записать

А = p ² 4 n ² R ²(m + 2M) - p ² n ² R ²(m + 2M) = 3 p ² n ² R ²(m + 2M).

№ 13. Материальная точка массой m = 0,01 кг совершает гармонические колебания по закону синуса с периодом Т = 2 с и начальной фазой j ₀, равной нулю. Полная энергия колеблющейся точки Е = 0,1 мДж.

Требуется: найти амплитуду А колебаний; написать закон данных колебаний x = f (t); найти наибольшее значение силы F _max, действующей на точку.

Р е ш е н и е.

1. Записать закон гармонических колебаний

x = A sin w t.

Так как закон не дает возможности определить амплитуду А, обратиться к условию задачи и воспользоваться полной энергией Е. Полная энергия колеблющейся точки Е равна, например, ее максимальной кинетической энергии Е _к,max.

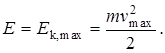
Скорость v колеблющейся точки определить, взяв первую производную смещения х по времени

.

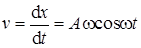Учесть, что v _max = Aw (cos j =1) и подставить это выражение в уравнение энергии Е _к,max

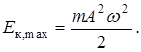
Найти амплитуду колебаний

.

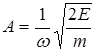Выразить амплитуду через период Т, учитывая что .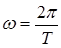

.

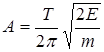Произвести вычисления

w = p с^-1

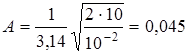м.

2. написать уравнение гармонических колебаний для данной точки:

х = 0,045sin pt.

3. записать второй закон Ньютона

| F _max| = ma.

Ускорение колеблющейся точки найти, взяв первую производную скорости по времени:

.

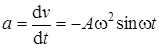Максимальное ускорение (при sin w t = 1)

| a _мах| = A w².

Записать выражение силы

| F _max| = mA w².

Произвести вычисления

F _max = 0,01×0,045×3,14² Н = 4,44 10^-3 Н.

№ 14. Складываются два колебания одинакового направления, заданные уравнениями:

x ₁ = cosp (t + 1/6),

x ₂ = 2cosp (t + 1/2)

(длина в см, время в с).

Требуется: Определить амплитуды, периоды и начальные фазы складывающихся колебаний; Написать уравнение результирующего колебания.

Р е ш е н и е.

1. Записать уравнение гармонического колебания в общем виде:

x = A cos (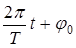). (1)

2. Привести заданные уравнения в соответствие с общим уравнением

х ₁ = A cos (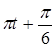), (2)

х ₂ = A cos (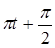). (3)

3. Сравнить уравнения (2) и (3) с (1). Из сравнения: А ₁ = 1см; А ₂ = 2 см.

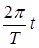= pt; 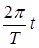= pt; Þ T ₁= 2c; T ₂ = 2c.

j ₀₁ = p / 6 рад = 30⁰; j ₀₂ = p / 2 рад = 90⁰.

Для написания уравнения результирующего колебания необходимо определить параметры результирующего колебания: T, А, j ₀.

1. Так как периоды колебаний одинаковы, период результирующего колебания будет тот же T = 2c.

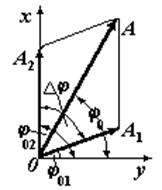
2. Для определения амплитуды результирующего колебания А удобно воспользоваться векторной диаграммой. В системе координат х0y отложить под углами, соответствующими начальным фазам, векторы амплитуд 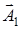и 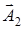. На них, как на сторонах, построить параллелограмм, диагональ которого и будет амплитудой результирующего колебания. Ее величину определить, используя теорему косинусов.

А =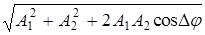

Подставить числовые значения

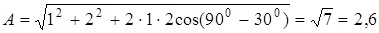см.

Начальную фазу результирующего колебания определить по тангенсу угла j ₀.

,

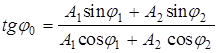откуда начальная фаза

.

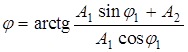Подставить данные

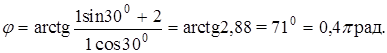
Таким образом параметры результирующего колебания найдены:

А = 2,6 см; Т = 2 с; j = 0,4 p рад.

Написать закон колебания

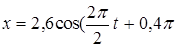) см

или

x = 2,6 cos p (t + 0,4) см.

№ 15. Материальная точка участвует одновременно в двух взаимно перпендикулярных гармонических колебаниях, уравнения которых имеют вид:

x = cos pt, (1)

y = 2cos 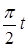, (2)

(амплитуда - в см, время - в с).

Определить траекторию точки и построить ее с соблюдением масштаба.

Р е ш е н и е.

Для определения траектории необходимо получить зависимость координат y = f(x). Для этого из уравнений (1) и (2) исключить время. Применив формулу косинуса половинного угла

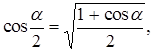
можно записать

y=2 .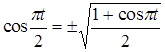

Так как cos p t = x (1), то

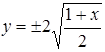; у = .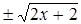

или

y ² = 2 +2 x.

х	у =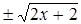
-1
-0,75	± 0,1
-0,5	± 1
	± 1,41
0,5	± 1,73
	± 2

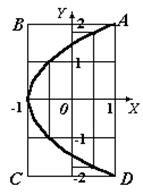
Полученное уравнение представляет собой уравнение параболы, ось которой лежит на оси Оx. Как показывают уравнения (1) и (2), амплитуда колебаний точки по оси Оx равна 1, а по оси Оy = 2. Следовательно, абсциссы всех точек траектории заключены в пределах от -1 до +1, а ординаты от -2 до +2.

Для построения траектории по уравнению (3) найти значения y, соответствующие ряду значений х, удовлетворяющих условию | x | £ 1.

Начертив координатные оси и выбрав масштаб, построить точки. Соединив их плавной кривой, получить траекторию точки. Она представляет собой часть параболы, заключенной внутри прямоугольника амплитуд АВСД. Из уравнений (1) и (2) находим периоды колебаний по горизонтальной и вертикальной осям Т _х и Т _у

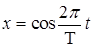, х = соs pt, y = 2cos .

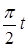t, с	x	y	положение точки
			положение А
	-1		вершина параболы
		- 2	положение D

Приравнивая аргументы, выразим Т _х

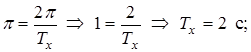аналогично - Т _у = 4 с.

Следовательно, когда точка совершит одно полное колебание по оси Оx, она совершит только половину полного колебания по оси Оy. После этого она будет двигаться в обратном направлении.

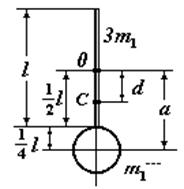
№ 16. Физический маятник представляет собой стержень длиной l = 1 м и массой 3 m ₁ с прикрепленным к одному из его концов обручем диаметром D = l /2и массой m ₁. Горизонтальная ось маятника проходит через середину стержня перпендикулярно ему. Определить период T колебаний этого маятника.

Р е ш е н и е.

1. Записать формулу периода колебаний физического маятника

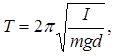(1)

где I - момент инерции маятника относительно оси колебаний; m - его масса; d - расстояние от центра масс маятника (точка С) до оси колебаний (точка О).

2. Определить момент инерции системы. Момент инерции маятника равен сумме моментов инерции стержня I ₁ и обруча I ₂

I = I ₁ + I ₂. (2)

Момент инерции стержня относительно оси, перпендикулярной стержню и проходящей через его центр масс, определить по формуле 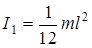. В данном случае m = 3m и

.

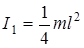Момент инерции обруча найти по теореме Штейнера

I ₂ = I ₀ + ma ²,

где I₂ = момент инерции обруча относительно произвольной оси; I ₀ - момент инерции, относительно оси, проходящей через центр масс обруча параллельно заданной оси; а - расстояние между указанными осями.

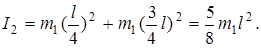
Найти момент инерции системы, подставив выражения I ₁ и I ₂ в формулу (2).

.

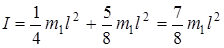3. Найти расстояние d от оси колебаний до центра масс маятника

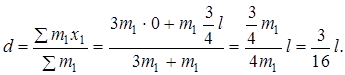
4. Определить период колебаний Т, подставив в формулу (1) момент инерции маятника I, расстояние d, массу системы (m = m ₁ +3 m ₁ = 4 m ₁).

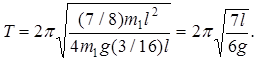
Т = 2,17 с.

№ 17. Волна распространяется по прямой со скоростью v = 20 м/с. Две точки, находящиеся на этой прямой на расстоянии l ₁ = 12 м и l ₂ = 15 м от источника волн, колеблются по закону синуса с одинаковыми амплитудами А = 0,1 м и с разностью фаз Dj = 0,75 p. Найти: длину волны l; написать уравнение волны; найти смещение указанных точек в момент времени t = 1,2 с.

Р е ш е н и е.

1. Точки, находящиеся друг от друга на расстоянии, равном длине волны l, колеблются с разностью фаз, равной 2 p; точки, находящиеся друг от друга на любом расстоянии D l, колеблются с разностью фаз

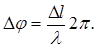
Решить это уравнение относительно l

,

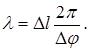где D l - расстояние между точками, равное 3 м.

Подставить значения величин

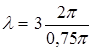= 8 м.

2. Записать уравнение плоской волны

s = A sin (w t – k x),

где к - волновое число 2p/ l,

или s = A sin w (t - ).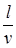

Найти циклическую частоту w,

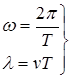решая систему относительно w, получаем

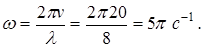
Написать уравнение волны

s = 0,1sin5 p (t - ).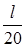

3. Найти смещение s, подставляя в это уравнение значения t и l.

s ₁ = 0,1sin5p(1,2 - 12/20) = 0,1sin3 p = 0;

s ₂ = 0,1sin5p(1,2 - 15/20) = 0,1sin2,25 p = 1sin0,25p = 0,071 м.

4.2. ТРЕНИРОВОЧНЫЕ ЗАДАЧИ

1. Точка движется по окружности радиусом R = 4 м. Закон ее движения выражается уравнением S = A + Bt ², где А = 6 м, В = -2 м/с². Найти момент времени t, когда нормальное ускорение точки а _n = 9 м/с², скорость v, тангенциальное ускорение а _t и полное ускорение точки а. (Ответ. 1,5 с; -6 м/c; -4 м/c²; 9,84 м/с²).

2. Две материальные точки движутся согласно уравнениям: x = A ₁ t +B ₁ t ² + C ₁ t ³ и x ₂ = A ₂ t + B ₂ t ² + C ₂ t ³, где А ₁ = 4 м/с; В ₁ = 8 м/с²; С ₁ = -16 м/с³; A ₂ = 2 м/c; B ₂ = -4 м/с²; С ₂ = 1 м/с³. В какой момент времени t ускорения этих точек будут одинаковыми? Найти скорости v ₁ и v ₂ точек в этот момент. (Ответ. 0,235 с; 5,1 м/с; 0,286 м/с).

3. Шар массой m ₁ = 10 кг сталкивается с шаром массой m ₂ = 4 кг. Скорость первого шара v ₁ = 4 м/c, второго - v ₂ = 12 м/с. Найти общую скорость u шаров после удара в двух случаях: 1) когда малый шар нагоняет большой шар, движущийся в том же направлении; 2) когда шары движутся навстречу друг другу. Удар считать прямым, центральным, неупругим. (Ответ. 6,28 м/с; -0, 573 м/с).

4. В лодке массой М = 240 кг стоит человек массой m = 60 кг. Лодка плывет со скоростью v = 2 м/с. Человек прыгает с лодки в горизонтальном направлении со скоростью u = 4 м/c (относительно лодки). Найти скорость лодки после прыжка человека: 1) вперед по движению лодка; 2) в сторону, противоположную движению лодки. (Ответ. 1м/с; 3 м/с).

5. Человек, стоящий в лодке, сделал шесть шагов вдоль нее и остановился. На сколько шагов передвинулась лодка, если масса лодки в два раза больше массы человека или в два раза меньше? (Ответ: 2 шага, 4 шага).

6. Из пружинного пистолета выстрелили пулькой, масса которой m = 5 г. Жесткость пружины к = 1,25 кН/м. Пружина была сжата на D l = 8 см. Определить скорость пульки при вылете из пистолета. (Ответ. 40 м/c).

7. Шар массой m ₁ = 200 г, движущийся со скоростью v ₁ = 10 м/с, ударяет неподвижный шар массой m ₂ = 800 г. Удар прямой, центральный, упругий. Определить скорости шаров после удара. (Ответ. -6 м/с; 4 м/с).

8. Шар, движущийся горизонтально, столкнулся с неподвижным шаром и передал ему 64% своей кинетической энергии. Шары упругие, удар прямой, центральный. Во сколько раз масса второго шара больше первого? (Ответ. в 4 раза).

9. Цилиндр, расположенный горизонтально, может вращаться около оси, совпадающей с осью цилиндра. Масса цилиндра m ₁ = 12 кг. На цилиндр намотали шнур, к которому привязали гирю массой m ₂ = 1 кг. С каким ускорением будет опускаться гиря? (Ответ. 1,4 м/с²; 8,4 Н).

10. Через блок, выполненный в виде колеса. Перекинута нить, к концам которой привязаны грузы m ₁= 100г и m ₂ = 300 г. Массу колеса считать равномерно распределенной по ободу, массой спиц пренебречь. Определить ускорение, с которым будут двигаться грузы, и силы натяжения по обе стороны блока. (Ответ. 3,27 м/с²; 1,31 Н; 1,9 Н).

11. Двум одинаковым маховикам, находящимся в покое, сообщили одинаковую угловую скорость w = 63 рад/с и предоставили их самим себе. Под действием сил трения первый маховик остановился через одну минуту, а второй сделал до полной остановки N = 300 об. У какого маховика тормозящий момент больше и во сколько раз? (Ответ. У первого больше в 1,2 раза).

12. Шар скатывается с наклонной плоскости высотой h = 90 см. Какую линейную скорость будет иметь центр шара в тот момент, когда шар скатится с наклонной плоскости? (Ответ. 3,55 м/с).

13. На верхней поверхности горизонтального диска, который может вращаться вокруг вертикальной оси, проложены по окружности радиуса r = 50 см рельсы игрушечной железной дороги. Масса диска М = 10 кг, его радиус R = 60 см. На рельсы диска был поставлен заводной паровозик m = 1 кг и выпущен из рук. Он начал двигаться относительно рельсов со скоростью и = 0.8 м/с. С какой угловой скоростью будет вращаться диск? (Ответ. 0,195 рад/с).

14. Платформа в виде диска вращается по инерции около вертикальной оси с частотой n ₁ = 14 об/мин. На краю платформы стоит человек. Когда человек перешел в центр платформы, частота возросла до n ₂ = 25 об/мин. Масса человека m = 70 кг. Определить массу платформы М Момент инерции человека рассчитывать, как для материальной точки. (Ответ. 210 кг).

15. Искусственный спутник вращается вокруг Земли по круговой орбите на высоте h = 3200 км над Землей. Определить линейную скорость спутника. (Ответ. 6,45 км/с).

16. Точка совершает гармонические колебания. В некоторый момент времени смещение точки х = 5 см, скорость v = 20 см/с и ускорение а = -80 см/с². Найти циклическую частоту и период колебаний, фазу колебаний в рассматриваемый момент времени и амплитуду колебаний. (Ответ. 4 с ^-1; 1,57 с; p /4 рад; 7,07 см).

17. Точка совершает гармонические колебания, уравнение которых имеет вид: х = А sin w t, где А = 5 см, w = 2 с^-1. Найти момент времени (ближайший к началу отсчета), в который потенциальная энергия точки Е _п =10^-4 Дж, а возвращающая сила F = 5×10^-3 Н. Определить также фазу колебаний в этот момент времени. (Ответ. 2.04 с; 4,07 рад).

18. Два гармонических колебания, направленных по одной прямой, имеющих одинаковые амплитуды и периоды, складываются в одно колебание той же амплитуды. Найти разность фаз складываемых колебаний. (Ответ. 120⁰ или 240⁰).

19. Точка совершает одновременно два гармонических колебания, происходящих по взаимно перпендикулярным направлениям и выражаемых уравнениями: х = A ₁cos w ₁t и y = A ₂cos w ₂(t + t), где А ₁ = 4 см; А ₂ = 8 см; w ₁ = p с^-1; w ₂ = p с^-1; t = 1 с. Найти уравнение траектории и начертить ее с соблюдением масштаба. (Ответ. 2 х + у = 0.).

20. Поперечная волна распространяется вдоль упругого шнура со скоростью v = 15 м/с. Период колебаний точек шнура Т = 1,2 с. Определить разность фаз Dj колебаний двух точек, лежащих на луче и отстоящих от источника волн на расстояниях х ₁ = 20 м и х ₂ = 30 м. (Ответ. 200⁰).

Дата добавления: 2014-12-16