Потенциальный барьер конечной ширины

План лекции

ОСОБЕННОСТИ ЭНЕРГЕТИЧЕСКОГО СПЕКТРА ЧАСТИЦ В СИСТЕМАХ ПОНИЖЕНОЙ РАЗМЕРНОСТИ

ЛЕКЦИЯ №3

1.1. Потенциальный барьер конечной ширины.

1.2. Интерференционные эффекты при надбарьерном пролете частиц.

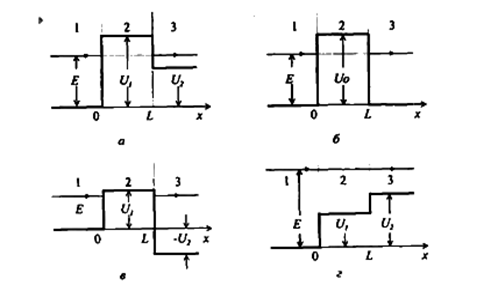
В реальной физической ситуации мы всегда имеем дело с барь­ером конечной ширины. Найдем коэффициенты отражения и про­хождения при движении частицы через прямоугольный потенци­альный барьер ширины I и высоты U₁ в предположении, что энер­гия частицы U ₂<Е< U ₁ (рис. 1.2, а).

Используя результаты разд. 1.1, можем сразу записать решения уравнения Шредингера для трех областей (1, 2 и 3):

(1.2.1)

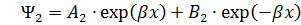
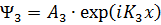
где К₁ , ,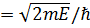

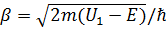При записи уравнений (1.2.1) учтено, что в области 3 нет ис­точников частиц и рассеивающих центров, т.е. будет распростра­няться только прошедшая волна.

Подставив (1.2.1) в (1.1. 10) и (1.1. 11), получим

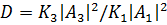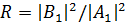, (1.2.2)

Амплитуды В₁ и A₃ найдем из системы линейных алгебраиче­ских уравнений, полученной с использованием условия непрерыв­ности волновой функции и ее первой производной на границе двух областей.

Так, при х = 0 имеем

А₁+В₁=А₂+В₂,

(1.2.3)

Рис. 1.2 Энергетическая диаграмма прямоугольного потенциального барьера

При x=L

(1.2.4)

Решив систему уравнений (1.2.3), (1.2.4), для несимметричного барьера (рис. 1.2,а) получим

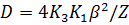, (1.2.5)

(1.2.6)

Отсюда для случая симметричного барьера (рис 1.2 б), когда K₁=K₃, запишем

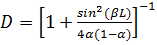(1.2.7)

(1.2.8)

Анализ выражений (1.2.5) и (1.2.7) показывает, что в случае барьера конечной ширины и высоты появляется конечная вероят­ность частице пройти под барьером, что абсолютно невозможно в классическом случае, так как при E<U₀ формально значение кине­тической энергии T становится отрицательным:

T = E-U₀<0.

Проникновение частицы с энергией E<U₀ через потенциальный барьер - чисто квантово-механический эффект, что видно из фор­мулы (1.2.5) (если положить в ней =0, получаем D=0). Это явле­ние носит название туннельного эффекта.

Отметим, что коэффициенты прохождения (1.2.5) и отражения (1.2.6) оказываются симметричными по индексам 1 и 3. Это озна­чает, что проницаемость барьера одинакова для потоков, па­дающих справа и слева. Из уравнения (1.2.5) также следует, что прошедший поток монотонно стремится к нулю, если либо К₁, либо К₃ стремится к нулю. Заметим также, что проведенный анализ и формулы (1.2.5), (1.2.6) могут быть распространены и на случай барьера, показанного на рис. 1.2, в, путем замены потенциала U₂ на (- U₂).

Дата добавления: 2014-11-28