Контрольной работы 2

МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ

Две первые задачи каждого варианта могут быть решены после усвоения тем 2.1 и 2.2. Прежде чем приступить к их решению, студент должен научиться безукоризненно владеть методом сечений для определения внутренних силовых факторов. Эти навыки пригодятся студентам для выполнения всех остальных задач второй контрольной работы и некоторых задач контрольной работы № 3.

Первая задача (задачи 61—70) требует от студента умения строить эпюры продольных сил, нормальных напряжений и опреде­лить удлинения или укорочения бруса.

При работе бруса на растяжение и сжатие в его поперечных сече­ниях возникает продольная сила N. Продольная сила в произвольном поперечном сечении бруса численно равна алгебраической сумме проекций на его продольную ось всех внешних сил, действующих на отсеченную часть.

Правило знаков для N: при растяжении продольная сила поло­жительна, при сжатии — отрицательна.

При растяжении (сжатии) бруса в его поперечных сечениях возни­кают нормальные напряжения σ = N/A (А — площадь поперечного сечения). Для нормальных напряжений принимается то же правило знаков, что и для продольных сил.

Изменение длины бруса (удлинение или укорочение) равно алгеб­раической сумме удлинений (укорочений) его отдельных участков и вычисляется по формуле Гука:

где N_i, l_i, A_i — соответственно продольная сила, длина и площадь сечения в пределах каждого участка бруса; Е — модуль продольной упругости.

Последовательность решения задачи:

1. Разбить брус на участки, начиная от свободного конца. Гра­ницами участков являются сечения, в которых приложены внешние силы, и места изменения размеров поперечного сечения.

2. Определить по методу сечений продольную силу для каждого участка (ординаты эпюры N), построить эпюру продольных сил N. Проведя параллельно оси бруса базовую (нулевую) линию эпюры, отложить перпендикулярно ей в произвольном масштабе получаемые значения ординат. Через концы ординат провести линии, проставить знаки и заштриховать эпюру линиями, параллельными ординатам.

3. Для построения эпюры нормальных напряжений определяем напряжения в поперечных сечениях каждого из участков. В пределах каждого участка напряжения постоянны, т. е. эпюра на данном участке изображается прямой, параллельной оси бруса.

4. Перемещение свободного конца бруса определяем как сумму удлинений (укорочений) участков бруса, вычисленных по формуле Гука.

Пример 1. Для данного ступенчатого бруса (рис. 1, а) построить эпюру продольных сил, эпюру нормальных напряжений и определить перемещение свободного конца, если Е = 2∙10⁵МПа;

F₁ = 30кН = 30∙10³ Н; F₂=38∙10³H; F₃ = 42кН = 42∙10³ Н;

А₁ = 1,9 см² = 1,9∙10²мм²

А₂= 3,1 см² = 3,1∙10²мм²

Решение. 1. Отмечаем уча­стки, как показано на рис. 1, а.

2. Определяем значения про­дольной силы N на участках бруса:

N _І= 0; N _ІІ= F₁ = 30 кН; N _ІІІ= F₁ = 30 кН; N _ІV= F₁ – F₂ = - 8 кН;

N _V= F₁ – F₂ –F₃ = - 50кН.

Строим эпюру продольных сил (рис. 1,б).

3. Вычисляем значения нор­мальных напряжений:

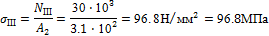
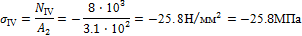
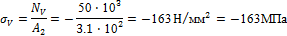
Строим эпюру нормальных напряжений (рис. 1, в).

5. Определяем перемещение свободного конца:

Рис. 1

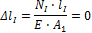
Δ l= Δ lІ + lІІ + lІІІ + Δ lІV + Δ lV Δ l= 0,394+0,0484-0,0516-0,161=0,23 мм Ответ: брус удлиняется на 0,23 мм.

Вторая задача (задачи 71 — 80) может быть решена студентами, если они будут ясно представлять смысл условия прочности при рас­тяжении (сжатии)

σ ≤ [ σ], где [σ]—допускаемое напряжение.

Необходимо знать, что исходя из условия прочности можно решать три вида задач: 1) проверка прочности σ = [σ];

2) проект­ный расчет (подбор сечения) [А]

3) определение допускае­мой нагрузки [N]≤А∙[σ].

В задачах 71 — 75 рассматриваются стержневые системы, работаю­щие на растяжение и сжатие, для которых необходимо выполнить проектный расчет, а также оценить прочность выбранного стандарт­ного сечения стержня. Стержни имеют одинаковые поперечные сечения.

Последовательность решения задачи:

1. Определить реакции стержней, используя уравнения равно­весия для плоской системы сходящихся сил и проверить правильность
найденных реакций.

2. Для наиболее нагруженного стержня, используя условие проч­ности [А] , определить площадь поперечного сечения стержня, подобрать по сортаменту (ГОСТ 8509—72) подходящий номер про­филя и найти стандартное значение площади поперечного сечения стержня.

3. Определить процент пере- или недогрузки наиболее нагружен­ного стержня, используя условие прочности σ≤[σ], при принятых
стандартных размерах площади поперечного сечения.

Пример 2, а. Для данной системы двух стержней одинакового по­перечного сечения, нагруженных силой F=170KH (рис. 2, а), опре­делить: а) требуемую площадь поперечных сечений стержней, состоя­щих из двух равнобоких уголков, и подобрать по ГОСТу (см. прило­жение II) соответствующий профиль уголка;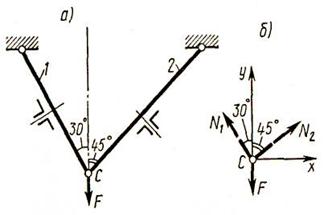

Рис. 2

2) определить процент пере- или недогрузки наиболее нагруженного стержня при принятых стандартных размерах сечения, приняв σ=140МПа.

Решение. 1. В данном примере в шарнире С приложена систе­ма сходящихся сил. Определяем силы N ₁и N ₂ в стержнях 1 и 2 (рис. 2, а), используя уравнения равновесия ΣХ = 0 и ΣY=0;

ΣX= - N₁sin30^o + N₂sin45^o = 0; (1)

ΣY = N₁cos30° + N₂cos45° = 0. (2)

Из (1):

(3)

Подставляем в уравнение (2) выражение (3) N ₁и получаем:

1,41 N ₂ ∙ cos 30° + N ₂∙cos 45° - F = 0;

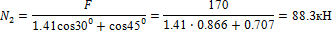
N₁ =1,41 N₂= 1,41∙88,3 = 124,5 кН.

Проверить правильность определения сил N ₁и N ₂можно так, как это показано в примере 1 методических указаний к контрольной работе № 1 по теоретической механике.

2. Определяем требуемую площадь поперечного сечения для наи­более нагруженного стержня:

N_max= N₁ = 124,5 кН; А

Площадь равнобокого уголка подбираем по значению А₁ /2= 8,89/2 = 4,445 см². Используя Приложение 2, назначаем профиль № 6,3 (63∙63∙4), площадью [А] = 4,96 см². Таким образом, требуемая площадь поперечного сечения стержней будет равна: 2[А] =2·4,96 = 9,92 см². Рабочее напряжение в поперечном сечении наиболее нагруженного стержня:

σ = 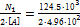= 125,5 Н/мм²= 125,5 МПа.

3.Проверяем прочность наиболее нагруженного стержня:

Недогрузка составляет 10,3%.

В задачах 76 —80 рассматривается система трех стержней одина­ковою поперечного сечения, поддерживающих абсолютно жесткую балку. Для наиболее нагруженного стержня следует найти допускае­мое значение силы F, которая приложена к данной системе.

Последовательность решения задачи:

1. Определить силы в стержнях, используя уравнения равновесия произвольной плоской системы сил, и сделать проверку правильности найденных реакций.

2. Определить допускаемое значение силы, нагружающей систему, используя условие прочности [N] ≤ А·[σ]. Стандартное значение пло­щади равнобокого уголка, заданного в условии задачи, взять по ГОСТу 8509—72 из Приложения 2.

Пример 2, б. Абсолютно жесткая балка (рис. 3, а) поддерживается тремя стержнями одинакового поперечного сечения, представляющего собой два равнобоких уголка с размерами 40∙40·4. Определить допускаемое значение силы F, если σ=160МПа. Весом балки пре­небречь.

Рис. 3

Решение. 1. Выбираем расчетную схему (рис. 3, а), представ­ляющую собой плоскую стержневую систему, для которой следует определить силы в стержне, используя уравнения равновесия произ­вольной плоской системы сил (рис. 3, б):

Σ M_D= - N₁·BD + F·AD = 0; (1)

Σ X = N₂ sin30^o – N₃ sin45^o = 0; (2)

Σ M_В =F·АB - N₂ cos30^o· BD – N₃ cos45⁰∙ BD = 0 (3)

Из (1):

N₁ = (4)

Из (2):

(5)

В уравнение (3) подставляем вместо N₂ выражение (5):

F·АB – 1,41∙ N₃ cos30^o· BD – N₃ cos45⁰∙ BD = 0(6)

Из (6)

(7)

Подставляя (7) в (5), получаем:

N₂ = 1,41 N₃ = 1,41 · 0.26 F = 0,366 F (8)

Проверяем правильность реакций N₁ , N₂, N₃.

Σ Y= - F – N₂ cos30⁰- N₃ cos45° + N₁ = -F - 0,366 ∙0,866 F – 0.26∙0.707 F + l,5 F =0.

Σ Y =0, следовательно, реакции стержней определены верно.

2. Так как все три стержня по условию имеют одинаковое попе­речное сечение (рис. 3, а), то допускаемое значение силы F опреде­ляем для наиболее нагруженного стержня, каким является стержень 1.

Следовательно, N_max=N₁= 1,5 F. Исходя из условия прочности:

[N] =1,5F = [σ]·2 A и учитывая, что площадь равнобокого уголка (40∙40·4) А = 3,08 см² (см. Приложение 2), получаем значение допус­каемой силы

Третья задача (задачи 81—90). К решению этой задачи сле­дует приступить после изучения темы «Кручение».

Кручением называют такой вид нагружения бруса, при котором в его поперечных сечениях возникает только один внутренний силовой фактор - крутящий момент М_к (или M_z).

Крутящий момент в произвольном поперечном сечении бруса равен алгебраической сумме внешних моментов, действующих на отсе­ченную часть:

М_к = Σ М_i (имеется в виду, что плоскости действия всех внешних скручивающих моментов M_i перпендикулярны продольной оси бруса).

Будем считать крутящий момент положительным, если для наблю­дателя, смотрящего на проведенное сечение, он представляется на­правленным по часовой стрелке. Соответствующий внешний момент направлен против часовой стрелки (рис.4).

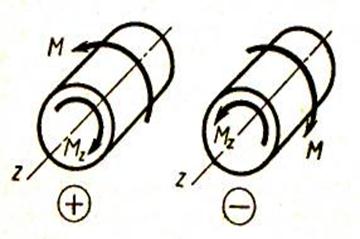Рис. 4

В третьей задаче необходимо выполнить проектный расчет вала круглого или кольцевого поперечно­го сечения из условий прочности и из условий жесткости; из двух полу­ченных значений диаметров следует выбрать наибольшее значение.

Последовательность решения задачи:

1. Определить внешние скручивающие моменты по формуле М = Р/ω, где Р - мощность, ω — угловая скорость.

2. Определить уравновешивающий момент, используя уравнение равновесия Σ М_i = 0, так как при равномерном вращении вала алгеб­раическая сумма приложенных к нему внешних скручивающих (вра­щающих) моментов равна нулю.

3. Пользуясь методом сечений, построить эпюру крутящих момен­тов по длине вала.

4. Для участка вала, в котором возникает наибольший крутящий момент, определить диаметр вала круглого или кольцевого сечения из условия прочности и жесткости. Для кольцевого сечения вала при­нять соотношение диаметров c=d_o/d, d_o — внутренний диаметр коль­ца; d — наружный диаметр кольца.

Из условия прочности:	Из условия жесткости:
где МZmax - наибольший крутящий момент; Wp — полярный момент сопротивления кручению; [τк] - допускаемое касательное напряжение.	1Р — полярный момент инерции сечения; G - модуль упругости при сдвиге; [φо] — допускаемый угол закручивания сечения.
Сечение вала — круг
Необходимый по прочности диаметр вала:	Необходимый по жесткости диаметр вала:
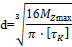
Сечение вала — кольцо
·(1 – с ^4)	·(1 – с ^4)
Необходимый по прочности наружный диаметр кольца:	Необходимый по жесткости на­ружный диаметр кольца:
Угол закручивания бруса (участка бруса), имеющего постоянное поперечное сечение, при условии, что крутящий момент во всех сечениях одинаков, определяется по формуле:

Пример 3. Для заданного стального бруса (рис. 5) требуется: 1) построить эпюру крутящих моментов; 2) определить из расчета на прочность и жесткость диаметр каждого из участков бруса, полагая по ва­рианту (а) поперечное сечение вала - круг; по варианту (б) - поперечное се­чение вала — кольцо, имеющее соотно­шение диаметров с = d_o/d = 0,8, принимая [τ_к] = 60 Н/мм² и [φ₀]=0,02 рад/м=0,02∙10^-3 рад/мм. Полученные по расчету значения диаметров округлить до ближайших четных или оканчива­ющихся на 5 чисел (в мм); 4) при принятых значениях диаметров рассчитать полный угол закручивания концевого сечения бруса. Принять М₁ =1,2 кН∙м; М₂ =1,7 кН∙м; G=8∙10⁴ МПа.

1,2

2,9

Эпюра М_Z [кН·м]

Рис. 5

Решение: 1. Определяем крутящий момент по участкам вала: М_Z1=М₁ =1,2 кН∙м; М_Z2 =М₁ + М₂ =1,2 +1,7 = 2,9 кН∙м; Строим эпюру крутящих моментов М_Z (рис. 5, б). 2. Исходя из эпюры М_Z: М_Zmax =2,9 кН∙м. 3. Определяем диаметр вала из условий прочности и жесткости:

а) Сечение вала – круг:

Из условия прочности: Принимаем d = 80 мм.

Из условия жесткости: Принимаем d = 66 мм.

Требуемый диаметр получился больше из расчета на прочность, поэтому его принимаем как окончательный d = 80 мм.

б) Сечение вала — кольцо:

Из условия прочности: Принимаем d = 95 мм.

Из условия жесткости: 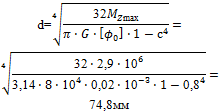Принимаем d = 75 мм.

Требуемые диаметры окончательно принимаем из расчетов на прочность: d = 95 мм, d₀ = 76 мм.

5. Определяем полярный момент инерции сечения:

Сечение вала – круг:	Сечение вала — кольцо:
	·(1 – с ^4)= =

6. Угол закручивания концевого сечения бруса: φ = φ₁ + φ₂

Сечение вала – круг:	Сечение вала — кольцо:
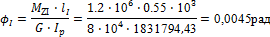
φ = φI + φII =0.0010 + 0.0020=0.0030 рад	φ = φI + φII =0.0045 + 0.0089=0.0134 рад

Четвертая задача (задачи 91—100). К решению этой задачи сле­дует приступить после изучения темы «Геометрические характеристики плоских сечений».

Последовательность решения задачи:

1. Определяют положение центра тяжести сечения.

2. Проводят центральные оси для каждого профиля проката. Эти оси называются центральными осями. Для первой фигуры проводят оси х₁ и у₁ для второй — х₂ и у₂ и т.д.

3. Проводят главные центральные оси. Они проходят через центр тяжести всего сечения. Одну из осей совмещают с осью симметрии (в задании все сечения имеют такую ось), а вторую проводят через центр тяжести сечения перпендикулярно первой. Вертикальная ось обозначается v, а горизонтальная — и.

4. Находят моменты инерции сечения относительно главных центральных осей. В общем виде моменты инерции сечения оп­ределяют по формулам:

относительно оси и

J _u =J ^I_u +J ^II_u +...+ J ⁿ_u

относительно оси v

J _v =J ^I_v +J ^II _v +...+ J ⁿ_v

где J_u и J_v — моменты инерции сечения относительно главных центральных осей и и v (главные центральные моменты инер­ции); J ^I_u ,J ^II_u , J ⁿ_u — моменты инерции простых фигур (1, 2,......, п) относительно главной центральной оси и; J ^I_v,J ^II _v ,J ⁿ_v ^— то же, относительно оси v.

Моменты инерции простых фигур относительно осей и и v определяются по формулам: относительно оси и

J ^I_{u =}J ^I_Х1 +а²₁А₁ ; J ^II_{u =}J ^II_Х2 +а²₂А₂ и т.д.

относительно оси v

J ^I _{v =}J ^I _Y1 +b²₁А₁ ; J ^II_{v =}J ^II _Y2 +b²₂А₂ и т.д.

где J_x1, J_x2,..,J_xn — моменты инерции простых фигур (1, 2,......, п) относительно собственных центральных осей х_1, х₂,..., х _n. Они определяются по таблицам ГОСТов (см. Приложения) для профи­лей прокатной стали и формулам для простых геометрических фи­гур (см. Приложения); J_y1,J_y2,..., J_yn — то же, относительно осей у_и ,у₂,..., у _п; а_1, а ₂,..., а _n— расстояние от главной центральной оси и до центральных осей х_1, х₂,..., х_п; b_1, b ₂,..., b _n — то же, от оси v до осей у₁, у₂,..., у_п; А₁, А₂..., А_п — площади сечений профилей про­катной стали или простых геометрических фигур.

Если главная центральная ось совпадает с собственной цен­тральной осью какого-нибудь профиля или фигуры, то момент инерции ее относительно главной центральной оси равен мо­менту инерции относительно собственной оси, так как расстоя­ние между ними равно нулю.

При определении геометрических характеристик необходимо учитывать, что профили проката на заданном сечении могут быть ориентированы иначе, чем в ГОСТах. Например, верти­кальная по ГОСТу ось у на заданном сечении может оказаться горизонтальной, а горизонтальная ось х — вертикальной. Поэто­му необходимо внимательно следить за тем, относительно каких осей следует брать геометрические характеристики. На это будет обращено особое внимание в рассматриваемых примерах.

Пример 4. Определить момент инерции сечения, показанного на рис. 6, относительно главной цен­тральной оси, не являющейся осью симметрии сечения. Сечение состо­ит из двутавра № 24 и швеллера № 24а.

Решение. 1. Центр тяжести сече­ния найден ранее (х_с = 6,11 см; у_с= 0).

2. Проведем центральные оси х_1, х₂ и у₁, у₂. Оси х₁ и х₂ совпали.

3. Проведем главные центральные оси. Ось и совмещаем сосью симметрии, а ось v проводим через центр тяжести С пер­пендикулярно оси и. Оси и, х₁ и х₂ совпали.

Рис. 6

4. Определим момент инерции сечения относительно оси v, так какпо условию требуется найти момент инерции только отно­сительно оси, не являющейся осью симметрии. Запишем фор­мулу

J _v =J ^I_v +J ^II _v

В этой формуле

J ^I _{v =} J ^I _Y1 +b²₁А₁ = 198 + (-6,11)² · 34,8 = 1497 см⁴;

J ^II_{v =}J ^II _Y2 +b²₂А₂ = 254 + (6,47)^2· 32,9 = 1631 см⁴,

где J ^I _Y1= 198см⁴; А₁ = 34,8см² (Приложение 1); J ^II _Y2 =254см⁴;

А₂ = 32,9см² (см. Приложение 3); b₁ = -6,11 см; b₂ = b _дв / 2+ b_шв – z_(0)шв=(11,5/2)+9,5 – 6,11--2,67=6,47 см (см. рис. 6).

Тогда J_v =1497+ 1631 = 3128 см⁴.

Ответ: J_v= 3128 см⁴.

Пятая задача (задачи 101—110).

К решению этой задачи сле­дует приступить после изучения темы «Изгиб».

Изгиб — это такой вид нагружения бруса, при котором в его поперечных сечениях возникают изгибающие моменты. В большинстве случаев одновременно с изги­бающими моментами возникают и поперечные силы; такой изгиб назы­вают поперечным: если поперечные силы не возникают, изгиб назы­вают чистым. Изгибающий момент М_И в произвольном поперечном сечении бруса численно равен алгебраической сумме моментов внеш­них сил, действующих на отсеченную часть, относительно центра тя­жести сечения: M_И = Σ М. Поперечная сила в произвольном попереч­ном сечении бруса численно равна алгебраической сумме внешних сил, действующих на отсеченную часть: Q = Σ F. Причем все внешние силы и моменты действуют в главной продольной плоскости бруса и расположены перпендикулярно продольной оси бруса.

Правило знаков для поперечной силы: силам, поворачивающим
отсеченную часть балки относительно рассматриваемого сечения по
ходу часовой стрелки, приписывается знак плюс (рис. 7, а), а силам,
поворачивающим отсеченную часть балки относительно рассматривае­мого сечения против хода часовой стрелки, приписывается знак минус
(рис. 7, б).

Правило знаков для изгибающих моментов: внешним моментом, изгибающим мысленно закрепленную в рассматриваемом сечении отсе­ченную часть бруса выпуклостью вниз, приписывается знак плюс (рис. 8, а), а моментам, изгибающим, отсеченную часть бруса выпук­лостью вверх, — знак минус (рис. 8, б).

Между изгибающим моментом М_Х, поперечной силой Q_У и интен­сивностью распределенной нагрузки q существуют дифференциальные зависимости:

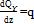
На основе метода сечений и дифференциальных зависимостей уста­навливается взаимосвязь эпюр М_Х и Q_У между собой и с внешней нагрузкой, поэтому достаточно вычислить ординаты эпюр для харак­терных сечений и соединить их линиями. Характерными являются сечения балки, где приложены сосредоточенные силы и моменты (вклю­чая опорные сечения), а также сечения, ограничивающие участки с равномерно распределенной нагрузкой.

Рис. 7 Рис. 8

Приведем некоторые правила построения эпюр.

Для эпюры поперечных сил:

1. На участке, нагруженном равномерно распределенной нагруз­кой, эпюра изображается прямой, наклоненной к оси балки.

2. На участке, свободном от распределенной нагрузки, эпюра изображается прямой, параллельной оси балки.

3. В сечении балки, где приложена сосредоточенная пара сил, поперечная сила не изменяет значения.

4. В сечении, где приложена сосредоточенная сила, значение поперечной силы меняется скачкообразно на значение, равное прило­женной силе.

5. В концевом сечении балки поперечная сила численно равна сосредоточенной силе (активной или реактивной), приложенной в этом сечении. Если в концевом сечении балки не приложена сосредоточен­ная сила, то поперечная сила в этом сечении равна нулю.

Для эпюры изгибающих моментов:

1. На участке, нагруженном равномерно распределенной нагруз­кой, эпюра моментов изображается квадратичной параболой. Выпук­лость параболы направлена навстречу нагрузке.

2. На участке, свободном от равномерно распределенной нагрузки, эпюра моментов изображается прямой линией.

3. В сечении балки, где приложена сосредоточенная пара сил, изгибающий момент меняется скачкообразно на значение, равное мо­менту приложенной пары.

4. Изгибающий момент в концевом сечении балки равен нулю, если в нем не приложена сосредоточенная пара сил. Если же в кон­цевом сечении приложена активная или реактивная пара сил, то изги­бающий момент в сечении равен моменту приложенной пары.

5. На участке, где поперечная сила равна нулю, балка испытывает чистый изгиб, и эпюра изгибающих моментов изображается прямой, параллельной оси балки.

6. Изгибающий момент принимает экстремальное значение в сече­нии, где эпюра поперечных сил проходит через нуль, меняя знаки с «+» на «—» или с «—» на «+».

В рассматриваемой задаче требуется построить эпюры поперечных сил и изгибающих моментов, а также подобрать размеры попереч­ного сечения балки, выполненной из прокатного профиля — двутавра.

Условие прочности для балок с сечениями, симметричными отно­сительно нейтральной оси, имеет вид:

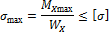
где W_Х — осевой момент сопротивления сечения.

Для подбора сечения балки (проектного расчета) из условия проч­ности определяют необходимое значение осевого момента сопротив­ления:

По найденному моменту сопротивления W_Х подбирают соответ­ствующее сечение по сортаменту (см. Приложение 1).

Для закрепленной одним концом балки строить эпюры целесооб­разно со свободного конца (чтобы избежать определения опорных реакций в заделке).

Последовательность решения задачи:

1. Балку разделить на участки по характерным сечениям.

2. Определить вид эпюры поперечных сил на каждом участке в зависимости от внешней нагрузки, вычислить поперечные силы в характерных сечениях и построить эпюру поперечных сил.

3. Определить вид эпюры изгибающих моментов на каждом участ­ке в зависимости от внешней нагрузки, вычислить изгибающие мо­менты в характерных сечениях и построить эпюру изгибающих мо­ментов.

4. Для данной балки, имеющей по всей длине постоянное попе­речное сечение, выполнить проектный расчет, т. е. определить W_Х в опас­ном сечении, где изгибающий момент имеет наибольшее по модулю значение.

Пример 5. Для заданной консольной балки (поперечное сече­ние—двутавр, [σ]=160МПа) построить эпюры Q_У и М_Х и подобрать сечение по сортаменту.

Решение. 1. Делим балку на участки по характерным сече­ниям А, В, С (рис. 9, а).

2. Определяем значения поперечной силы Q_У в характерных се­чениях и строим эпюру (рис. 9, б):

3. Определяем значения изгибающего момента М_Х в характерных
сечениях и строим эпюру (рис. 9, в):

Рис. 9

М_А =0;

4. Исходя из эпюры М_Х (рис. 9, в)

М_{Х max} = 15 кН∙м =15∙10⁶ Н·мм;

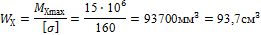
В соответствии с ГОСТ 8239—72 выбираем двутавр № 16 (см. При­ложение 1).

Шестая задача (задачи 111 — 120). Для того чтобы решить пятую задачу, необходимо внимательно изучить тему «Изгиб», методические указания к задаче 4, а также приведенный далее пример.

Последовательность решения задачи та же, что и пятой. Отли­чие лишь в том, что шестую задачу начинают решать с определения реакций опор балки и проверки правильности найденных реакций.

Пример 6. Для заданной двухопорной балки (рис. 10, а) опре­делить реакции опор, построить эпюры поперечных сил, изгибающих моментов и определить размеры поперечного сечения (h, b, d) в форме прямоугольника или круга, приняв для прямоугольника h/b =1,5. Счи­тать [σ] = 160 МПа.

Рис. 10

Решение. 1. Определяем опорные реакции и проверяем их найденные значения:

Σ М_D = 0; Σ M_D = M₁ - F₂∙CD - M₂ - R_B·BD + F_l∙OD = 0;

Σ М _В =0; ΣM_B= F₁· OB - M₂+F₂∙BC +R_D·BD + М₁ = 0;

Так как реакция R_D получилась со знаком минус, то изменяем ее первоначальное направление на противоположное. Истинное направле­ние реакции R_d — вниз (рис. 10, б).

Проверка: ΣY = - F + R_B + F₂ —R_D = — 18+ 10 + 30 - 22 = 0.

Условие статики ΣY = 0 выполняется, следовательно, реакции опор определены верно. При построении эпюр используем только истинные направления реакций опор.

2. Делим балку на участки по характерным сечениям О, В, С, D
(рис. 10, б).

3. Определяем в характерных сечениях значения поперечной силы Q_Y
и строим эпюру слева направо (рис. 10, в):

Q₀^ПР = - F₁ = -18кН;

Q_В^ЛЕВ = - F₁ = - 18 кН;

Q_В^ПР = -F₁ + R_B = -18+10= - 8кН;

Q_С^ЛЕВ = -F₁ + R_B= -18+10= - 8кН;

Q_С^ПР = -F_l + R_B+F₂ = - 18+ 10 + 30 = 22 кН;

Q_D^ЛЕВ = - F ₁ + R_B + F₂ = 22 кН.

4. Вычисляем в характерных сечениях значения изгибающего мо­мента М_Х и строим эпюру (рис. 10, г):

М₀ = 0; М_В= - F₁ · AB= - 18∙5= - 90кН·м;

М_С^ЛЕВ = -F₁· OC + R_B·BC= -18·9+10·4= - 122 кН · м;

М_С^ПР = —F₁ · OC + R_B·BC + M₂= -18·9+10·4+10= -112 кН · м;

М_D^ЛЕВ = - F₁· OD + R_В ·BD + M₂ + F₂· CD = -18·15+10·10 + 10 + 30·6= 20 кН·м.

5. Вычисляем размеры сечения данной балки из условий прочности
на изгиб по двум вариантам: а) сечение — прямоугольник с заданным
соотношением сторон (рис. 10, е); б) сечение — круг (рис. 10, д). Вы­числение размеров прямоугольного сечения:

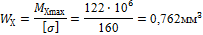
Используя формулу и учитывая, что h = 1,5b, нахо­дим

Используя формулу 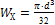, находим диаметр круглого сечения

Дата добавления: 2014-12-16