Багатовимірне ранжування статистичної сукупності

Ранжування – це встановлення відповідної послідовності розміщення одиниць статистичної сукупності за допомогою попарного їхнього порівняння. Впорядкування одиниць сукупності (ранжування) згідно з рангами (пріоритетами) дає змогу визначати перевагу однієї одиниці перед іншою, встановлювати їхню належність до певної групи. Ранжування широко застосовують для оцінювання привабливості різних інвестиційних проектів, якості і сертифікації продукції, показників соціально-економічного розвитку та ін.

У тому разі, коли кожна одиниця статистичної сукупності відображена лише однією ознакою, упорядкування можна виконати, замінивши значення ознаки відповідними рангами. Якщо одиниця сукупності характеризується декількома ознаками, виникає потреба в обчисленні інтегральної оцінки одиниці сукупності – комплексного показника, який характеризує властивість одиниці сукупності в найзагальнішій формі її прояву, враховуючи сумарну дію значень різних за своєю суттю ознак.

Нехай сукупність складається з n одиниць, кожна з яких описується значеннями m ознак, а х_іj – значення j-ої ознаки для і-ої одиниці сукупності. Тоді значення ознак і-ої одиниці сукупності можна задати вектором 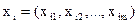. Перетворення векторних величин на скалярні (інтегральні оцінки) 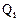називають агрегуванням (скаляризацією). Агрегування ознак ґрунтується на теорії “адитивної цінності”, згідно з якою цінність цілого еквівалентна сумі цінностей його складових.

Визначення інтегральної оцінки передбачає виконання таких процедур:

• вибір множини ознак;

• вибір методу стандартизації ознак;

• вибір методу агрегування стандартизованих ознак.

Формування множини ознак полягає у виборі ознак, значення яких відіграють вагому роль у визначенні загальної властивості одиниці сукупності. Воно повинно відбуватися на підставі якісного аналізу статистичної сукупності або на основі номенклатури ознак загальноприйнятих систем класифікації техніко-економічної інформації, соціальних і демографічних явищ тощо. Наприклад, щоб визначити інтегральну оцінку рівня якості металорізального верстата для порівняння його з базовою моделлю множина ознак може містити такі показники: річна продуктивність у разі безвідмовної роботи (тис.год.); частка простоювань через відмову (%); вартість верстата (тис.грн.); річні витрати на ремонт (тис.грн.); інші річні експлуатаційні витрати (тис.грн.); термін служби (років).

Для забезпечення інформаційної спрямованості показників їх поділяють на стимулятори 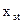і дестимулятори . Стимулятори прямо впливають на інтегральну оцінку 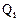, а дестимулятори – обернено. У разі агрегування дестимулятори перетворюються на стимулятори і навпаки за допомогою таких співвідношень:

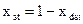, (2.1)

або

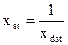. (2.2)

Здебільшого ознаки мають різні одиниці вимірювання, у зв’язку з чим адитивне агрегування вимагає приведення їх до однієї основи. Цю процедуру називаютьстандартизацією, згідно з якою вектор первинних значень ознак і-ої одиниці сукупності 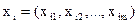замінюють на вектор стандартизованих значень .

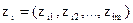Існують різні методи стандартизації, але всі вони передбачають відносне зіставлення емпіричних значень показника з певними величинами (А, q):

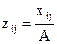, (2.3)

або

. (2.4)

Як А вибирають 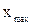, , 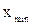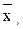або (еталонне значення j-ої ознаки), а q являє собою одиницю стандартизації.

Інтегральну оцінку 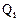для ознак з однаковою вагомістю визначають за такою формулою:

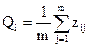
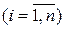, (2.5)

а для ознак з різною вагомістю за іншою формулою:

, (2.6)

де 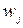- вага j-ої ознаки, причому 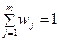, 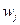>0.

Якщо для техніко-економічних показників, які характеризують властивості одиниці статистичної сукупності, існують стандарти або інші нормативні значення 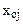, упорядкування сукупності можна виконати за допомогою інтегральної оцінки рівня відхилення від еталону. Стандартизовані значення розраховують за такою формулою:

. (2.7)

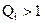Порівняльний (рейтинговий) аналіз часто здійснюють на підставі інтегральної оцінки, зіставляючи значення ознак із середніми (). Очевидно, що при рівень розвитку (інтенсивності) явища в і-ій одиниці сукупності перевищує середній у сукупності, а при 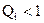- нижчий за середній.

Рейтинг окремих одиниць сукупності може бути встановлений також на підставі стандартизованих значень, які визначають за такою формулою:

, (2.8)

де 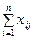- загальний обсяг значень j-ої ознаки в сукупності, 0< <1.

Тоді інтегральна оцінка і-ої одиниці сукупності буде дорівнювати:

. (2.9)

Стандартизовані значення можна розрахувати на підставі відхилень значень ознаки від мінімального і максимального значень показника в сукупності за такими формулами:

- для стимуляторів ; (2.10)

- для дестимуляторів . (2.11)

Значення 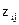при цьому показує позицію і-ої одиниці сукупності в діапазоні варіації за j-ою ознакою. Якщо j-та ознака набуває великих значень, то 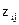наближається до 1, а в протилежному випадку – до 0. Тому, чим вищий рівень ознак і-ої одиниці сукупності, тим більшого значення набуває інтегральна оцінка .

Приклад 2.1. З урахуванням техніко-економічних параметрів металорізальних верстатів (табл.2.1), визначити інтегральні оцінки їхньої якості.

Таблиця 2.1

Марка верстата	Вартість, тис.грн.	Річна продуктивність, тис.грн.	Річні експлуатаційні витрати, тис.грн.	Термін служби, роки
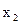
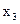
А	75,35	25,50	2,60
Б	97,80	26,70	2,80
В	110,60	28,00	3,10
Г	85,00	26,00	2,50

Показники та є стимуляторами, а та 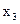- дестимуляторами. Для стандартизації значень ознак скористаємося залежностями (2.10) і (2.11). Матриця стандартизованих значень має вигляд:

.

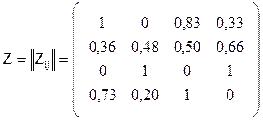Допустимо, що показникам , та 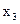надається вага , а 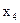- вага . Тоді з урахуванням (2.6) отримаємо такі інтегральні оцінки обладнання:

;

;

;

.

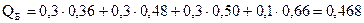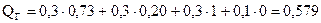Розраховані вище інтегральні показники свідчать, що найкращим можна вважати металорізальний верстат А.

Відносну позицію і-ої одиниці у статистичній сукупності можна встановити за допомогою таксономічного показника, який визначають за формулою:

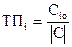, (2.12)

де - відстань, яка характеризує позицію і-ої одиниці сукупності відносно вибраної бази порівняння; 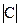- відстань між верхньою і нижньою точками діапазону (стандартний діапазон варіації ознак).

Для обчислення таксономічного показника спочатку виконують стандартизацію відхилень від середньої:

- для стимуляторів 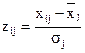; (2.13)

- для дестимуляторів , (2.14)

де - середнє квадратичне відхилення j-ої ознаки у статистичній сукупності.

Розраховують інтегральну оцінку з використанням стандартного діапазону варіації для всіх ознак на одному й тому ж рівні:

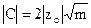, (2.15)

де - точка, взята за базу порівняння.

Наприклад, якщо за базу порівняння вибрати , а ознакова множина складається з 4-х елементів, то .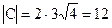

Позицію і-ої одиниці сукупності відносно вибраної бази порівняння можна тлумачити як евклідову відстань:

. (2.16)

Якщо за базу порівняння вибрана нижня межа діапазону варіації, то чим більшим є значення таксономічного показника, тим вищою є інтенсивність прояву явища в одиниці сукупності.

Дата добавления: 2014-12-16