Основи кластерного аналізу

До методів кластерного аналізу належать методи класифікації багатовимірної статистичної сукупності, які ґрунтуються на понятті відстані між досліджуваними об’єктами. Для формування груп (кластерів) однорідних одиниць у кожний кластер включають подібні згідно з вибраною просторовою метрикою одиниці сукупності.

Термін “кластерний аналіз” (cluster – згусток – англ.) запропонований К.Тріоном. У загальному випадку методи кластерного аналізу (автоматичної класифікації, розпізнавання образів без навчаючої вибірки, таксономії, як їх ще називають) розв’язують задачу оптимального поділу початкової множини статистичних спостережень 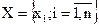на k підмножин (кластерів, класів, таксонів) 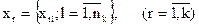згідно з вибраним критерієм якості. Переважно кількість кластерів k наперед невідома.

Найвживанішими у практиці кластерного аналізу вважають хеммінгову та евклідову міри відстані.

Хеммінгову відстань застосовують для ознак, що набувають лише значення 0 або 1. Її обчислюють за такою формулою:

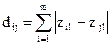, (2.19)

де 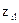і 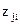- стандартизовані значення l-ої ознаки в і-ій та j-ій одиниці сукупності.

Звичайну евклідову відстань застосовують для кількісних ознак з однаковими ваговими коефіцієнтами. Її обчислюють за такою формулою:

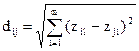. (2.20)

Зважену евклідову відстань застосовують для кількісних ознак, які мають різну вагу. Її обчислюють за модифікованою формулою (2.20):

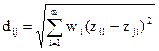, (2.21)

де 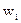- вага 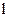-ої ознаки.

З урахуванням способів формування кластерів розрізняють ітеративні та ієрархічні методи кластерного аналізу.

В основу ітеративних методів покладено оптимізацію вибраного показника якості класифікації. Попередньо виконують деякий орієнтовний поділ статистичної сукупності на класи, для кожного з яких визначають багатовимірні середні (центри тяжіння).

Після цього розраховують відстані окремих одиниць сукупності до центрів тяжіння кластерів. Одиницю сукупності приєднують до того кластера, відстань до центра тяжіння якого є найменшою. Далі розраховують нові центри тяжіння і процедуру формування кластерів повторяють. Як наслідок, мінімізують внутрішньогрупові дисперсії і забезпечують однорідність сформованих кластерів.

Серед ієрархічних методів кластерного аналізу найчастіше застосовують агломеративні методи – послідовне об’єднання двох найближчих кластерів. Початково вважають, що кожна одиниця сукупності становить окремий кластер. Інформаційною базою кластерної процедури слугує матриця відстаней між кластерами, розмірність якої на кожному кроці об’єднання кластерів понижується на одиницю. Найближчі кластери – це кластери, яким відповідає мінімальний елемент у матриці відстаней. Після об’єднання кластерів здійснюють коригування матриці відстаней за одним з алгоритмів:

• одиничного зв’язку (“найближчого сусіда”);

• повного зв’язку (“найдальшого сусіда”);

• середнього зв’язку.

У першому випадку за відстань між кластерами беруть відстань між найменш віддаленими елементами кластерів, а у другому – між найвіддаленішими елементами кластерів. Алгоритм середнього зв’язку використовує середню відстань між елементами кластеру.

Під час формування кластерів можна застосовувати обмеження, зміст яких полягає у заданні максимально можливих відстаней між елементами кластера. Елементи, які не відповідають таким обмеженням, треба зарахувати до різних кластерів.

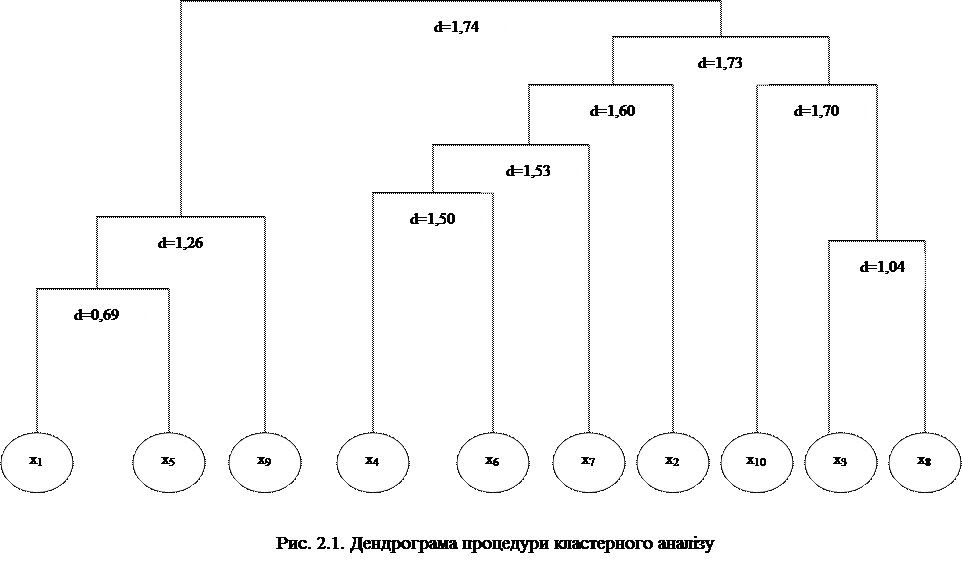
Результати кластерного аналізу можна подавати у вигляді таблиць (матриць), які містять основні характеристики статистичних ознак у кластерах, або у вигляді деревоподібних діаграм (дендрограм), які репрезентують розподіл одиниць сукупності на групи під час окремих кроків виконання процедури кластерного аналізу. На одній осі дендрограми відкладають номери одиниць статистичної сукупності, а на другій – відстані, за якими їх об’єднують у кластери.

Приклад 2.2. Користуючись агломеративною процедурою, здійснити класифікацію десяти фірм, показники маркетингової діяльності яких подані у табл.2.2.

Таблиця 2.2

Порядковий номер фірми	Обсяг продажу, млн.грн.	Рентабельність, %	Співвідношення “якість-ціна”, балів
х1	х2	х3

Продовження табл.2.2

Для формування матриці відстаней виконаємо стандартизацію змінних. Для цього знаходимо:

; ;

; ;

; .

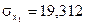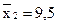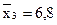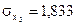Матриця стандартизованих значень змінних має вигляд:

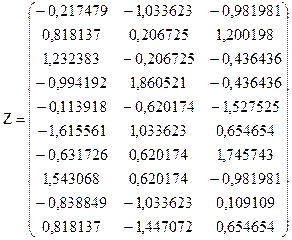
Результати проміжних розрахунків для процедури кластеризації згідно з ієрархічним методом (ознаки вважаються рівновагомими, а об’єднання кластерів здійснюється за алгоритмом одиничного зв’язку) відображено в табл.2.3. Розподіл одиниць сукупності за групами під час виконання кроків кластерного аналізу наведено на рис.2.1.

Таблиця 2.3

Результати процедури кластерного аналізу

Іте-ра- ція	Клас-тери	Евклідова відстань між кластерами
												Мінімальна відстань: d(1,5)=0,692304
2,715302 1,755985 3,045812 0,692304 2,984411 3,216694 2,415486 1,255618 1,980407	1,738135 2,949262 2,998827 2,627597 1,603328 2,336316 2,339774 1,741454	3,038279 1,781556 3,292374 2,986732 1,038222 2,295949 1,703097	2,849422 1,503442 2,536089 2,876416 2,949206 3,926217	3,1228 3,538484 2,140487 1,837127 2,512845	1,52622 3,581404 2,274732 3,475159	3,488582 2,335918 2,750651	3,098233 2,73452	1,792808
	1,5	1,5									Мінімальна відстань: d(3,8)=1,038222
2,715302 1,755985 2,849422 2,984411 3,216694 2,140487 1,255618 1,980407	1,738135 2,949262 2,627597 1,603328 2,336316 2,339774 1,741454	3,038279 3,292374 2,986732 1,038222 2,295949 1,703097	1,503442 2,536089 2,876416 2,949206 3,926217	1,52622 3,581404 2,274732 3,475159	3,488582 2,335918 2,750651	3,098233 2,73452	1,792808

Продовження табл.2.3

	1,5 3,8	1,5		3,8						Мінімальна відстань: d(1,5; 9)=1,255618
2,715302 1,755985 2,849422 2,984411 3,216694 1,255618 1,980407	1,738135 2,949262 2,627597 1,603328 2,339774 1,741454	2,876416 3,292374 2,986732 2,295949 1,703097	1,503442 2,536089 2,949206 3,926217	1,52622 2,274732 3,475159	2,335918 2,750651	1,792808
	1,5,9 3,8	1,5,9		3,8					Мінімальна відстань: d(4,6)=1,503442
2,339774 1,755985 2,849422 2,274732 2,335918 1,792808	1,738135 2,949262 2,627597 1,603328 1,741454	2,876416 3,292374 2,986732 1,703097	1,503442 2,536089 3,926217	1,52622 3,475159	2,750651
	1,5,9 3,8 4,6	1,5,9		3,8	4,6			Мінімальна відстань: d(4,6; 7)=1,52622
2,339774 1,755985 2,274732 2,335918 1,792808	1,738135 2,627597 1,603328 1,741454	2,876416 2,986732 1,703097	1,52622 3,475159	2,750651

Закінчення табл.2.3

	1,5,9 3,8 4,6,7	1,5,9		3,8	4,6,7		Мінімальна відстань: d(4,6,7; 2)=1,603328
2,339774 1,755985 2,274732 1,792808	1,738135 1,603328 1,741454	2,876416 1,703097	2,750651
	1,5,9 3,8 4,6,7,2	1,5,9	3,8	4,6,7,2		Мінімальна відстань: d(3,8; 10)=1,703097
1,755985 2,274732 1,792808	1,738135 1,703097	1,741454
	1,5,9 3,8,10 4,6,7,2	1,5,9	3,8,10	4,6,7,2	Мінімальна відстань: d(3,8,10; 4,6,7,2)=1,738135
1,755985 2,274732	1,738135
	1,5,9 3,8,10,4,6,7,2	1,5,9	3,8,10,4,6,7,2
1,738135

Дата добавления: 2014-12-16