Вторая итерация

Для второй итерации в качестве начального значения вектора весовых коэффициентов используется значение, полученное на конечном шаге первой итерации.

5.12. Выполняются пункты 5.2 – 5.11. Если по результатам второй ите-рации не достигается выполнения условия непревышения предельно допус-тимых ошибок обучения, проводится третья итерация и так до тех пор, пока на будет выполнено условие непревышения ошибок обучения для всех воз-можных входных векторов. По достижении этого условия обучение выбран-ного нейрона заканчивается.

6. Выбирается следующий нейронный элемент и сигнал, на который этот элемент должен быть настроен.

7. Выполняются п.п. 4 – 12 для обучения выбранного нейронного элемента.

8. Выполняются п.п. 6.- 7 для обучения всех нейронных элементов сети.

9. Путем подачи на вход сети всех распознаваемых образов подтверждается единичная реакция каждого нейронного элемента только на входной сигнал, соответствующий образу, распознаваемым данным элемен-том. В случае ошибочного решения, принимаемого сетью, выполнить про-верку правильности приведения расчетов, выполняемых при проектирова-нии.

6.2.4. Пример. Выполнить проектирование сети, предназначенной для распознавания двух образов, при условии, что на входе сети кроме распоз-наваемых объектов может присутствовать и мешающий образ.

1. Проводится анализ задания на проектирование. Выполняется кодиро-вание (при необходимости) входной информации. Определяется размерность входного вектора и необходимое для решения задачи распознавания число нейронов.

Представим распознаваемые образы и мешающий образ в виде кодиро-ванных последовательностей, в которых единицей будем кодировать заштри-хованные квадратики, а нулем – незаштрихованные. В соответствии с вы-бранным типом кодирования образы могут быть представлены кодами:

распознаваемые объекты – 1100 и 1010, мешающий объект – 1001 (выбор порядка кодирования произволен, но одинаков для всех образов).

Так как размерность кодов во всех случаях одинакова и равна 4, то раз-мерность входного вектора принимается равной 4. В связи с тем, что число распознаваемых полезных образов равно 2, то число нейронов в сети выбира-ется равным 2.

2. Разрабатывается структурная схема нейронной сети. Осуществляется закрепление каждого из нейронов за распознаваемым образом.

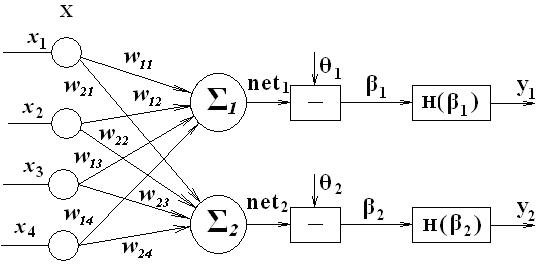
Рис. 7

Будем считать, что первый нейрон должен обеспечить распознавание первого образа, а второй – второго.

3. Выбирается правило расчета весовых коэффициентов.

Расчет вектора весовых коэффициентов в процессе обучения производится в соответствии с выражением

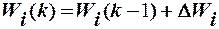
где 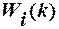- рассчитываемое значение вектора весовых коэффициентов на к-том шаге, 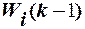- значение вектора весовых коэффициентов, полученное на предыдущем шаге, 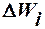- корректирующее слагаемое, получаемое в соответствии с выражением

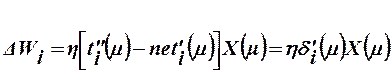
где ……….(расписать входящие обозначения)

4. Выполним выбор параметров первого нейронного элемента.

Примем значение коэффициента обучения h=0,6.

Пороговое значение θ₁=2, так как число единиц в коде, соответству-ющем первому образу равно 2.

Определим желаемые реакции первого нейрона на полезный образ и мешающие для него образы как

t´´_{1жел пол} (1) = θ₁ + ∆

и t´´_{1жел меш} (2,3) = θ₁ -∆.

Выберем ∆= 0,5 (так как само значение θ₁ небольшое).

Тогда t´´_{1жел пол} (1) =2,5, а t´´_{1жел меш} (2,3) = 1,5.

Максимально допустимые ошибки обучения δ_{max пол} и δ_{max меш} примем равными 0,1.

5. Расчет вектора весовых коэффициентов первого нейронного элемен-та.

5.1. Зададим следующие начальные значения компонент вектора весо-вых коэффициентов:

w₁₁=0,3; w₁₂=0,6; w₁₃=0,5; w₁₄=0,8.

5.2. На вход сети подаем первый сигнал, код которого равен 1100.

5.3. Для заданного начального значения весового вектора для первого сигнала (μ=1) определяется сетевая функция

net´₁(1)= ,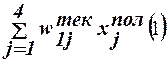

где в качестве текущих значений составляющих весового вектора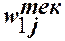

выбираются их начальные значения.

net´₁(1)=0,3•1+0,6•1+0,5•0+0,8•0=0,9

5.4. Определяем ошибку обучения в соответствии с выражением.

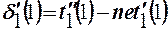
где 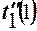= t´´_{1жел пол} (1) =2,5.

С учетом этого 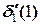=2,5-0,9=1,6.

5.5. Полученное значение ошибки обучения больше, чем δ_{max пол} =0,1.

Поэтому выполним коррекцию вектора весовых коэффициентов в соответст-вии с выражением

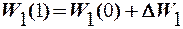
где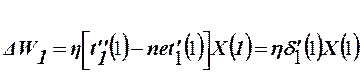

Тогда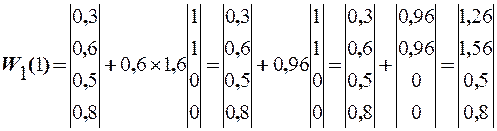

5.6. На вход сети подается сигнал, характеризующий второй (мешаю-щий) образ, код которого равен 1010.

5.7. С учетом скорректированного значения весового вектора для второго сигнала определяется сетевая функция

net´₁(2)= ,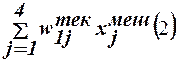

где в качестве текущих значений составляющих весового вектора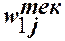

выбираются их скорректированные значения.

net´₁(2)=1,26•1+1,56•0+0,5•1+0,8•0=1,76

5.8. Определяем ошибку обучения в соответствии с выражением

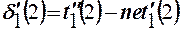
где 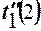= t´´_{1жел меш} (2) = 1,5.

С учетом этого 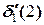=1,5-1,76=-0,26.

5.9. Полученное значение ошибки обучения больше, чем δ_{max меш} =0,1. Поэтому выполним коррекцию вектора весовых коэффициентов в соответст-вии с выражением

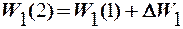
где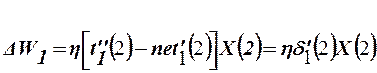

Тогда

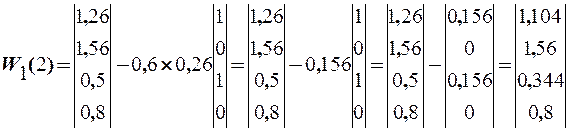
5.10. На вход сети подается сигнал, характеризующий третий (мешаю-щий) образ, код которого равен 1001.

5.11. С учетом скорректированного значения весового вектора для третьего сигнала определяется сетевая функция

net´₁(3)= ,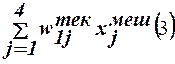

где в качестве текущих значений составляющих весового вектора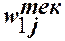

выбираются их скорректированные ранее в пункте 5.9 значения.

net´₁(3)=1,104•1+1,56•0+0,344•0+0,8•1=1,904

5.12. Определяем ошибку обучения в соответствии с выражением

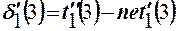
где 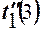= t´´_{1жел меш} (2) = 1,5.

С учетом этого 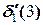=1,5-1,904=-0,404.

5.13. Полученное значение ошибки обучения больше, чем

δ_{max меш} =0,1.

Поэтому выполним коррекцию вектора весовых коэффициентов в соот-ветствии с выражением

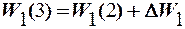
где

Тогда

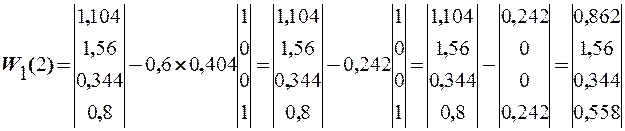
Так как не на одном из шагов не было достигнуто выполнение условия не-превышения получаемой ошибки обучения предельно допустимой, перехо-дим ко второй итерации.

Вторая итерация.

5.14. На вход сети подаем первый сигнал, код которого равен 1100.

5.15. Для полученного на первой итерации значения весового вектора определяется сетевая функциядля первого сигнала (μ=1)

net´₁(1)= ,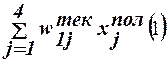

где в качестве текущих значений составляющих весового вектора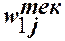

выбираются их значения, полученные на первой итерации.

net´₁(1)=0,862•1+1,56•1+0,344•0+0,558•0=2,422

5.16. Определяем ошибку обучения в соответствии с выражением.

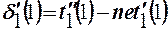
где 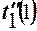= t´´_{1жел пол} (1) =2,5.

С учетом этого 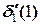=2,5-2,422=0,078.

5.17. Полученное значение ошибки обучения меньше, чем δ_{max пол} =0,1. Поэтому значение вектора весовых коэффициентов не изменяем.

5.18. На вход сети подается сигнал, характеризующий второй (мешаю-щий) образ, код которого равен 1010.

5.19. С учетом значения весового вектора определяется сетевая функ-ция для второго сигнала

net´₁(2)= ,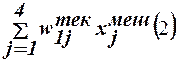

где в качестве текущих значений составляющих весового вектора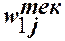

выбираются их значения, полученные на предыдущем шаге.

net´₁(2)=0,862•1+1,56•0+0,344•1+0,558•0=1,206

5.20. Определяем ошибку обучения в соответствии с выражением

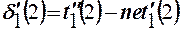
где 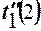= t´´_{1жел меш} (2) = 1,5.

С учетом этого 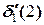=1,5-1,206=0,294.

5.21. Полученное значение ошибки обучения больше, чем

δ_{max меш} =0,1. Поэтому выполним коррекцию вектора весовых коэффици-ентов в соответствии с выражением

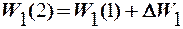
где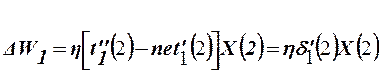

Тогда

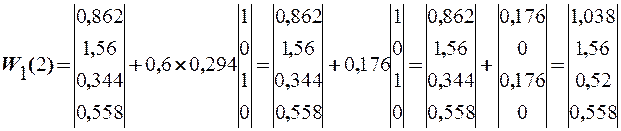
5.22. На вход сети подается сигнал, характеризующий третий (мешаю-щий) образ, код которого равен 1001.

5.23. С учетом скорректированного значения весового вектора для третьего сигнала определяется сетевая функция

net´₁(3)= ,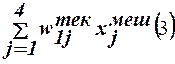

где в качестве текущих значений составляющих весового вектора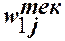

выбираются их скорректированные ранее в пункте 5.9 значения.

net´₁(3)=1,038•1+1,56•0+0,52•0+0,558•1=1,596

5.24. Определяем ошибку обучения в соответствии с выражением

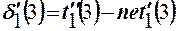
где 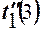= t´´_{1жел меш} (2) = 1,5.

С учетом этого 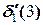=1,5-1,596=-0,096.

5.25. Полученное значение ошибки обучения меньше, чем

δ_{max меш} =0,1. Поэтому значение вектора весовых коэффициентов не изме-няем.

Так как на одном из шагов не было достигнуто выполнение условия непревышения получаемой ошибки обучения предельно допустимой, пере-ходим к третьей итерации.

5.26.Процесс продолжается до тех пор, пока для всех сигналов ошибки обучения не будут превышать максимально допустимые ошибки.

5.27. После окончания процесса обучения первого нейрона переходим к обучению второго нейрона. Этот процесс полностью аналогичен процессу обучения первого нейронного элемента за исключением того, что полезным для него считается уже второй сигнал, а первый выступает уже в качестве мешающего наряду с третьим сигналом. В соответствии с этим изменяются и желаемые результаты, то есть

t´´_{2жел пол} (2) = θ₂ + ∆,

t´´_{2жел меш} (1,3) = θ₂ -∆.

и при θ₂=2 и∆= 0,5

t´´_{2жел пол} (2) = 2,5,

t´´_{2жел меш} (1,3) = 1,5.

5.28. После окончания определения векторов весовых коэффициентов для обоих нейронных элементов производим проверку правильности работы сети путем подачи на её вход всех распознаваемых образов и удостоверяем-ся, что единичная реакция каждого элемента наблюдается только в том слу-чае, когда на входе сети присутствует сигнал, для распознавания которого обучался данный нейрон.

Дата добавления: 2014-12-16