Слой Гроссберга

Слои Кохоненна

НОРМАЛЬНОЕ ФУНКЦИОНИРОВАНИЕ

В своей простейшей форме слой Кохонена функционирует в духе «победи-тель забирает все», т. е. для данного входного вектора один и только один нейрон Кохонена выдает на выходе логическую единицу, все остальные вы-дают ноль.

Каждый нейрон слоя Кохонена соответствует структурной схеме, при-веденной на рис.1 при выборе в качестве функции преобразования функции Хевисайда.

Ассоциированное с каждым нейроном Кохонена множество весов соеди-няет его с каждым входом. Например, на рис. 8 нейрон Кохонена К₁ имеет веса w₁₁, w₁₂, …, w_1m, составляющие весовой вектор W ₁. Они соединяются через входной слой с входными сигналами х ₁, x ₂, …, x _m, составляющими входной вектор X. Подобно нейронам большинства сетей выход net_i каждо-го i-того нейрона Кохонена является просто суммой взвешенных входов. Это может быть выражено следующим образом:

(25)

или в векторной записи

N = W^TX, (26)

где N – вектор выходов сетевых функций net слоя Кохонена.

Нейрон Кохонена с максимальным значением net является «победителем». Его выходу присваивается значение, равное единице, а остальным - ноль.

Слой Гроссберга функционирует в сходной манере. Его выход net является взвешенной суммой выходов k₁,k₂,..., k_n слоя Кохонена, образующих вектор К. Вектор соединяющих весов, обозначенный через V, состоит из весов v₁₁, v ₁₂,..., v _pn. Тогда выход net_j каждого нейрона Гроссберга есть

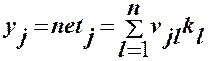, (27)

Y = KV,

где Y – выходной вектор слоя Гроссберга, К – выходной вектор слоя Кохоне-на, V – матрица весов слоя Гроссберга.

Если слой Кохонена функционирует таким образом, что лишь у одного нейрона значение величины net равно единице, а у остальных равна нулю, то лишь один элемент вектора К отличен от нуля, и вычисления очень прос-ты. Фактически каждый нейрон слоя Гроссберга лишь выдает величину веса, который связывает этот нейрон с единственным ненулевым нейроном Кохо-нена.

Дата добавления: 2014-12-16