
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Решение задач ЛП не обладающих очевидным начальным базисом двухэтапным симплекс-методом
|
|
|
|
Симплекс-метод решения задач ЛП, обладающих очевидным начальным базисом и заданных в каноническом виде
Задача 3. Решить задачу линейного программирования, заданную в каноническом виде и имеющую очевидный начальный базис:
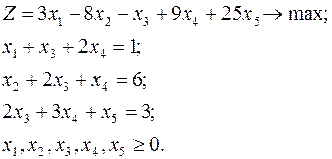
Выпишем матрицу ограничений:
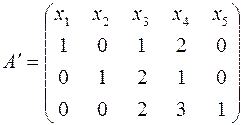 .
.
Очевидный начальный базис 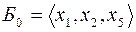 , т.к. путем перестановки столбцов при этих переменных получается единичная подматрица.
, т.к. путем перестановки столбцов при этих переменных получается единичная подматрица.
Выражаем из ограничений базисные переменные 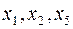 через небазисные:
через небазисные: 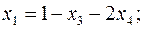
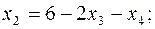
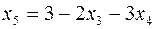 и подставляем в
и подставляем в 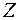 :
:
. 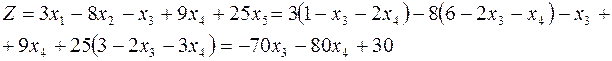
Переносим неизвестные влево:
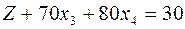 - Z-строка начальной симплекс-таблицы.
- Z-строка начальной симплекс-таблицы.
Строим начальную симплекс-таблицу (смотрите таблицу 4).
Таблица4
| Б | Z | x1 | x2 | x3 | x4 | x5 | Реш. | 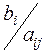
| Ком. |
| Z | - | Опт. | |||||||
| x1 | - | ||||||||
| x2 | - | ||||||||
| x5 | - |
Данная симплекс-таблиц оптимальна,. Получаем
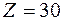 - максимальное значение при значениях переменных:
- максимальное значение при значениях переменных:
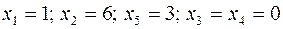 .
.
Проверка:
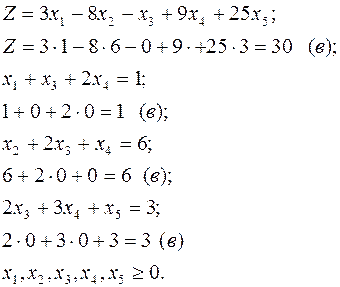
Задача 4. Предприятие может производить 3 вида продукции 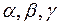 . Для их производства используются 2 вида ресурсов А и В, запасы которых
. Для их производства используются 2 вида ресурсов А и В, запасы которых 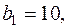
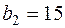 . Прибыль от реализации единицы продукции
. Прибыль от реализации единицы продукции 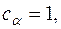
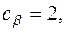
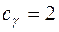 .
.
Технологическая матрица имеет вид:
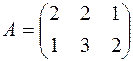 .
.
Рынок показывает, что продукт 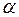 должен производиться в объеме не менее 5 единиц.
должен производиться в объеме не менее 5 единиц.
Требуется найти оптимальный план производства 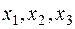 , при котором выполняются все ограничения и прибыль
, при котором выполняются все ограничения и прибыль 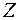 максимальна.
максимальна.
Получаем задачу ЛП:
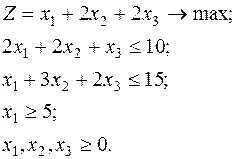 (1)
(1)
Приведем (1) к каноническому виду, вводя остаточные переменные:
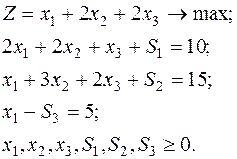 (2)
(2)
Выписывает расширенную матрицу ограничений для (2):
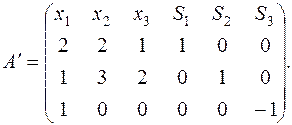
Т.к. в матрице 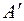 нет столбца вида
нет столбца вида 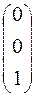 матрице
матрице 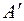 нет, поэтому в 3-ем ограничении отсутствует очевидная базисная переменная и данная задача не имеет очевидного базиса.
нет, поэтому в 3-ем ограничении отсутствует очевидная базисная переменная и данная задача не имеет очевидного базиса.
Первый этап. На первом этапе решается вспомогательная 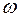 - задача, целью решения которой является нахождение начального базиса
- задача, целью решения которой является нахождение начального базиса 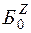 основной
основной 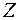 - задачи.
- задачи.
Вводим ряд искусственных переменных 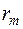 , количество которых равно количеству недостающих базисных переменных и рассматриваем новую целевую функцию:
, количество которых равно количеству недостающих базисных переменных и рассматриваем новую целевую функцию: 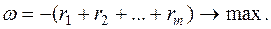
Математическая модель задачи:
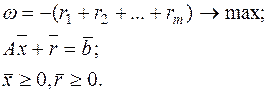 (3),
(3),
где 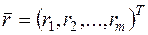 – вектор искусственных переменных.
– вектор искусственных переменных.
Вводим в 3-е ограничение вводим искусственную переменную 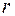 и решаем задачу вида:
и решаем задачу вида:
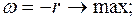
при ограничениях:
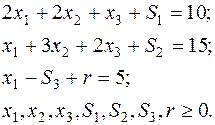 (4)
(4)
Выписываем расширенную матрицу ограничений для (4):
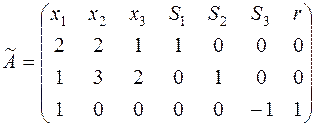
Так как в матрице 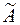 есть единичная подматрица, образованная столбцами при переменных
есть единичная подматрица, образованная столбцами при переменных 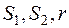 , следовательно
, следовательно 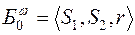 - очевидный начальный базис для
- очевидный начальный базис для 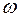 - задачи.
- задачи.
Выражаем базисную переменную 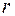 из ограничения и исключаем из целевой функции:
из ограничения и исключаем из целевой функции: 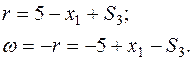
Переносим неизвестные влево:
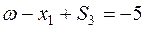 - w - строка начальной симплекс-таблицы.
- w - строка начальной симплекс-таблицы.
Строим начальную симплекс-таблицу (таблица 5) w - задачи и доводим ее до оптимальной.
Таблица 5
| Б | ω | x1 | x2 | x3 | S1 | S2 | S3 | r | Реш. | bi/ai | Комм. |
| ω | -1 | -5 | - | не опт. | |||||||
| S1 | х1→Б | ||||||||||
| S2 | Б→r | ||||||||||
| r | -1 | ||||||||||
| w | - | опт. | |||||||||
| S1 | -2 | - | |||||||||
| S2 | -1 | - | |||||||||
| X1 | -1 | - |
Т.к. 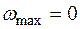 , значит, I этап завершен успешно, и искусственная переменная
, значит, I этап завершен успешно, и искусственная переменная 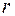 выведена из базиса.
выведена из базиса.
Второй этап. На II этапе в качестве начального базиса основной задачи принимаем оптимальный базис вспомогательной задачи, т.е. 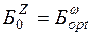 .Возвращаемся к целевой функции
.Возвращаемся к целевой функции 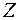 исходной задачи, и столбцы искусственных переменных
исходной задачи, и столбцы искусственных переменных 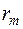 удаляем из симплекс-таблицы.
удаляем из симплекс-таблицы.
Выражаем базисную переменную 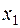 из оптимальной симплекс- таблицы и исключаем из целевой функции
из оптимальной симплекс- таблицы и исключаем из целевой функции 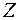 :
:
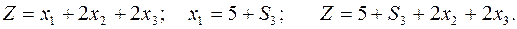
Переносим неизвестные влево: 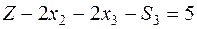 –
– 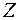 - строка начальной симплекс-таблицы основной задачи.
- строка начальной симплекс-таблицы основной задачи.
Строим начальную симплекс-таблицу основной задачи и доводим ее до оптимальной (таблица 6).
Таблица 6
| Б | Z | x1 | x2 | x3 | S1 | S2 | S3 | Реш. | bi/ai | Ком. |
| Z | -2 | -2 | -1 | - | Не опт. | |||||
| S1 | x3→Б | |||||||||
| S2 | Б→S1 | |||||||||
| x1 | -1 | - | ||||||||
| Z | - | Опт. | ||||||||
| x3 | - | |||||||||
| S2 | -1 | -2 | -3 | - | ||||||
| x1 | -1 | - |
Имеем:
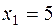 – объем производства I – го продукта.
– объем производства I – го продукта.
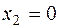 – II продукт не производится.
– II продукт не производится.
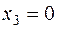 – III продукт не производится.
– III продукт не производится.
S1 = 0 – ресурс А используется полностью.
S2 = 10 – остаток ресурса В.
S3 = 0 – превышение производства продукта 1 над плановым заданием.
Замечание 4. Если 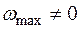 , тогда исходная задача несовместима; переход ко 2-му этапу не осуществляется;
, тогда исходная задача несовместима; переход ко 2-му этапу не осуществляется;
Экономическая интерпретация алгоритма симплекс-метода и оптимальной симплекс-таблицы
Задача 5. Предприятие может выпускать 3 различных вида продукции, цены реализации которых равны соответственно 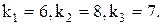 При производстве используются два вида ресурсов запасы, которых
При производстве используются два вида ресурсов запасы, которых 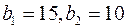 , а цены закупки единицы ресурса
, а цены закупки единицы ресурса 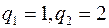 .
.
Технологическая матрица имеет вид:
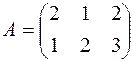 .
.
Определить оптимальный план работы предприятия, дать экономический анализ для каждой итераций поиска решения с помощью симплекс-метода.
Решение.
Пусть 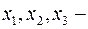 искомые объемы производства продуктов 1,2,3.
искомые объемы производства продуктов 1,2,3.
Найдем по формуле (1) ценовые коэффициенты переменных 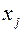 в функции прибыли.
в функции прибыли.
Имеем:
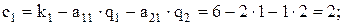
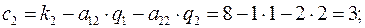
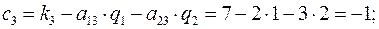
таким образом, производство продуктов 1,2 рентабельно, производство продукта 3 нерентабельно.
Задача ЛП о нахождении оптимального плана имеет вид:
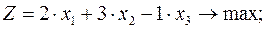
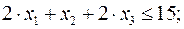
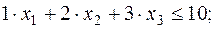
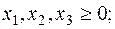
Приведем задачу (10) к каноническому виду:
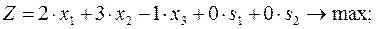
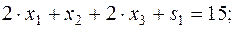
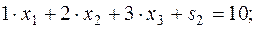
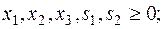
Начальный базис задачи: 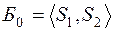 .
.
Z – строка начальной симплекс-таблицы 7:
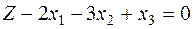 .
.
Таблица 7
| Б | Z | x1 | x2 | x3 | S1 | S2 | Реш. | bi/aij | Ком. |
| Z | -2 | -3 | - | Не опт. | |||||
| S1 | x2→Б | ||||||||
| S2 | Б→S2 |
Экономический анализ:
Производства нет: 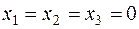 .
.
Прибыль равна 0: 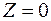 .
.
Остатки ресурсов их запасам: 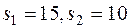 .
.
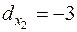 => план не оптимален, целесообразно включить в производство продукт 2, при этом прибыль составит 3руб. на 1 ед. дополнительного производства продукта 2 т.е.
=> план не оптимален, целесообразно включить в производство продукт 2, при этом прибыль составит 3руб. на 1 ед. дополнительного производства продукта 2 т.е. 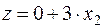 .
.
При увеличении 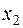 остатки ресурсов уменьшаются:
остатки ресурсов уменьшаются:
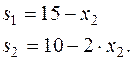
Максимально возможный объём производства продукта. 2:
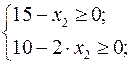 →
→ 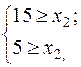 →
→ 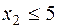 →
→ 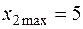 .
.
Следовательно, производство продукта 2 можно увеличить до 5 ед. При этом ресурс 2 расходуется полностью: 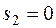 , а остаток ресурса составит:
, а остаток ресурса составит: 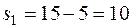 ед. Новый план производства представлен в таблице 8.
ед. Новый план производства представлен в таблице 8.
Таблица 8
| Б | Z | x1 | x2 | x3 | S1 | S2 | Реш. | bi/aij | Ком. |
| Z | -1/2 | 11/2 | 3/2 | - | Не опт. | ||||
| S1 | 3/2 | 1/2 | -1/2 | 20/3 | x2→Б | ||||
| x2 | 1/2 | 3/2 | 1/2 | Б→S2 |
Экономический анализ:
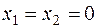 - продукты 1 и 3 не производятся,
- продукты 1 и 3 не производятся,
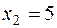 - объём производства продукта 2;
- объём производства продукта 2;
 - размер получаемой прибыли.
- размер получаемой прибыли.
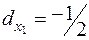 => план не оптимален; целесообразно увеличивать производство продукта 1, при этом прибыль увеличивается на 0.5 руб. на 1 ед. увеличения производства продукта 1, т.е.
=> план не оптимален; целесообразно увеличивать производство продукта 1, при этом прибыль увеличивается на 0.5 руб. на 1 ед. увеличения производства продукта 1, т.е. 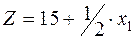 .
.
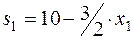 , остаток ресурса 1 идет на производство продукта 1.
, остаток ресурса 1 идет на производство продукта 1.
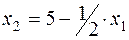 - производство продукта 2 уменьшается, т.к. необходимо освободить часть ресурса 2 для производства продукта 1.
- производство продукта 2 уменьшается, т.к. необходимо освободить часть ресурса 2 для производства продукта 1.
Максимально возможный объём производства продукта. 2:
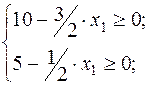 →
→ 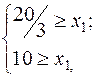 →
→ 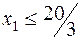 →
→ 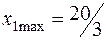 .
.
Следовательно, производство продукта 1 можно увеличить до 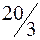 ед. При этом ресурс 1 расходуется полностью:
ед. При этом ресурс 1 расходуется полностью: 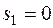 , а объём производства товара 2 уменьшится до:
, а объём производства товара 2 уменьшится до: 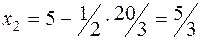 ед.
ед.
Оптимальный план производства представлен в таблице 9.
Таблица 9
| Б | Z | x1 | x2 | x3 | S1 | S2 | Реш. | bi/aij | Ком. |
| Z | 17/3 | 1/3 | 4/3 | 55/3 | - | опт. | |||
| x1 | 1/3 | 2/3 | -1/2 | 20/3 | - | ||||
| x2 | 4/3 | -1/3 | 2/3 | 5/3 | - |
Экономический анализ:
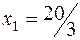 - производство продукта 1;
- производство продукта 1;
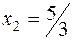 - производство продукта 2;
- производство продукта 2;
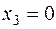 - продукт 3 не производится.
- продукт 3 не производится.
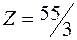 - максимальная прибыль.
- максимальная прибыль.
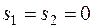 - ресурсы используются полностью.
- ресурсы используются полностью.
Экономический анализ ресурсов:
Таблица 10
| Ресурс | Отаток | Статус | Ценность | Комментарий |
| дефицит | 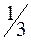
| Цена на ресурс может возрасти не более чем на 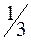 руб., но его выгодно будет использовать Закупка 1 ед. ресурса по текущей цене и включение в производство дает дополнительную прибыль руб., но его выгодно будет использовать Закупка 1 ед. ресурса по текущей цене и включение в производство дает дополнительную прибыль 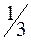 руб. руб.
| ||
| дефицит | 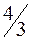
| Цена на ресурс может возрасти не, более чем на 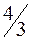 руб., но его выгодно будет использовать. Закупки 1 ед. ресурса по текущей цене и включение в производство дает дополнительную прибыль руб., но его выгодно будет использовать. Закупки 1 ед. ресурса по текущей цене и включение в производство дает дополнительную прибыль 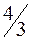 руб. руб.
|
Вывод: В первую очередь стоит приобретать ресурс 2 как более ценный.
Экономический анализ продуктов:
Таблица 11
| Продукт | Статус | Относительная оценка в опт плане | Комментарий |
| базисный | Выгодный, производится в объеме 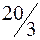 и дает вклад в прибыль и дает вклад в прибыль 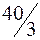 руб. руб.
| ||
| базисный | Выгодный, производится в объеме 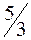 и дает вклад в прибыль и дает вклад в прибыль 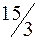 руб. руб.
| ||
| не базисный | 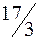
| Не производится. Убыток от производства 1 ед. продукта по сравнению с опт. планом составит 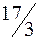 руб. Производство станет выгодным, если цена реализации увеличивается, по крайней мере, на руб. Производство станет выгодным, если цена реализации увеличивается, по крайней мере, на 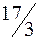 руб. руб.
|
Транспортная задача линейного программирования
Задача 6. На двух складах хранится однородный товар в объёмах 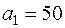 ,
, 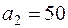 . Его необходимо доставить в четыре магазина, потребности которых b1=30, b2=30, b3=20, b4=20. Удельные транспортные затраты на перевозки:
. Его необходимо доставить в четыре магазина, потребности которых b1=30, b2=30, b3=20, b4=20. Удельные транспортные затраты на перевозки: 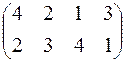 . Для данной задачи составить оптимальный план перевозок.
. Для данной задачи составить оптимальный план перевозок.
Определим тип задачи:
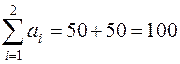 - суммарные запасы;
- суммарные запасы;
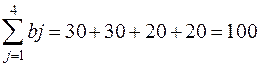 - суммарные потребности.
- суммарные потребности.
Т.к. 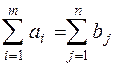 , то задача закрытая.
, то задача закрытая.
Если выполняется неравенство 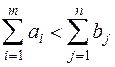 - транспортная задача называется открытой транспортной задачей с избыточным спросом. Она может быть приведена к закрытой задаче, если ввести в рассмотрение условного поставщика
- транспортная задача называется открытой транспортной задачей с избыточным спросом. Она может быть приведена к закрытой задаче, если ввести в рассмотрение условного поставщика 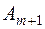 , величина запасов у которого:
, величина запасов у которого: 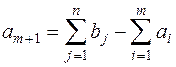 , а удельные транспортные затраты по перевозке груза от условного поставщика ко всем потребителям принимаются равными 0:
, а удельные транспортные затраты по перевозке груза от условного поставщика ко всем потребителям принимаются равными 0: 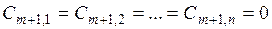 . Компоненты
. Компоненты 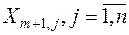 найденного плана поставок означают количество товара, которое недополучит потребитель
найденного плана поставок означают количество товара, которое недополучит потребитель 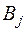 .При этом матрица планирования транспортной задачи дополняется одной строкой.
.При этом матрица планирования транспортной задачи дополняется одной строкой.
Если выполняется неравенство 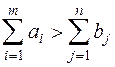 - транспортная задача называется открытой транспортной задачей с избыточным предложением. Она может быть приведена к закрытой задаче, если ввести в рассмотрение условного потребителя
- транспортная задача называется открытой транспортной задачей с избыточным предложением. Она может быть приведена к закрытой задаче, если ввести в рассмотрение условного потребителя 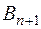 , величина запасов у которого:
, величина запасов у которого: 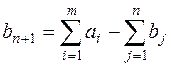 , а удельные транспортные затраты по перевозке груза от условного поставщика ко всем потребителям принимаются равными 0:
, а удельные транспортные затраты по перевозке груза от условного поставщика ко всем потребителям принимаются равными 0: 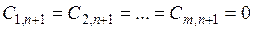 . Компоненты
. Компоненты 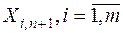 , найденного плана поставок означают количество товара, которое останется у поставщика
, найденного плана поставок означают количество товара, которое останется у поставщика 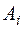 после того как потребности всех потребителей будут удовлетворены. При этом матрица планирования транспортной задачи дополняется одним столбцом
после того как потребности всех потребителей будут удовлетворены. При этом матрица планирования транспортной задачи дополняется одним столбцом
Определим тип задачи:
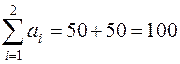 - суммарные запасы;
- суммарные запасы;
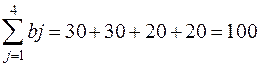 - суммарные потребности.
- суммарные потребности.
Т.к. 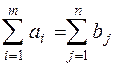 , то задача закрытая.
, то задача закрытая.
Не учитывая удельные транспортные затраты на перевозку груза, начинаем удовлетворять потребности 1-го потребителя B1 за счёт 1-го поставщика A1. Потребности потребителя B1 удовлетворены, а у поставщика A1 осталось 20 ед. товара, поэтому за счёт A1 пытаемся удовлетворить потребности B2 (переходим на клетку вправо). На складе A1 товара не осталось, а потребности B2 не удовлетворены, поэтому удовлетворяем его потребности за счёт склада А2 (перемещаемся на клетку вниз). Потребности В2 удовлетворены, а на складе А2 осталось 40 ед. товара, поэтому удовлетворяем за счёт его потребности В3 (переходим на клетку вправо). Потребности В3 удовлетворены, а на складе А2 осталось 20 ед. товара, поэтому удовлетворяем за счёт его потребности В4 (переходим на клетку вправо). Всего 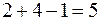 базисных клеток.
базисных клеток.
Начальный план перевозок, полученный методом северо-западного угла, представлен в таблице 12:
Таблица 12
| 4 30 |  2 20 2 20
| 1 | 3 | |
| 2 | 3 10 | 4 20 | 1 20 | |
Клетка называется занятой, если в ней находится какой-либо объём перевозок. Базисом транспортной задачи называется набор 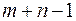 занятых клеток, обладающих следующим свойством: в каждой строке и в каждом столбце должна быть хотя бы одна базисная клетка. Потенциалами строк и столбцов относительно базиса Б называется набор чисел
занятых клеток, обладающих следующим свойством: в каждой строке и в каждом столбце должна быть хотя бы одна базисная клетка. Потенциалами строк и столбцов относительно базиса Б называется набор чисел 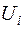 ,
, 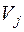 , удовлетворяющие уравнению:
, удовлетворяющие уравнению:
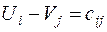 , если
, если 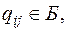 (1)
(1)
где 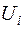 - потенциал
- потенциал  -ой строки;
-ой строки; 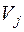 - потенциал
- потенциал 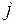 -ого столбца.
-ого столбца.
После того как найдены потенциалы строк и столбцов определяем относительные оценки небазисных клеток по формуле:
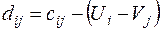 , если
, если 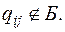 (2)
(2)
Если нет 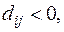 то текущий план оптимален.
то текущий план оптимален.
Проверим на оптимальность начальный план перевозок, представленный в таблице 12.
По базисным клеткам по формуле (1) составим систему уравнений для определения потенциалов строк и столбцов:
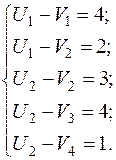
Эта система содержит 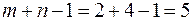 уравнений с
уравнений с 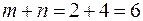 неизвестными. Т.к. уравнений на 1 меньше чем неизвестных, система является неопределённой и одному неизвестному (которое чаще всего встречается) присваивают нулевое значение. После этого остальные потенциалы определяются однозначно.
неизвестными. Т.к. уравнений на 1 меньше чем неизвестных, система является неопределённой и одному неизвестному (которое чаще всего встречается) присваивают нулевое значение. После этого остальные потенциалы определяются однозначно.
Пусть 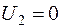 , тогда
, тогда 
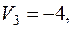
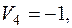
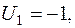
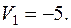
Вычисляем по формуле (2) относительные оценки небазисных клеток:
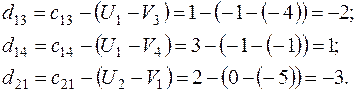
Т.к. есть 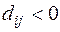 , текущий план не оптимален.
, текущий план не оптимален.
В таблице 13 представлен начальный план перевозок, проверенный на оптимальность:
Таблица 13
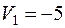
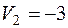
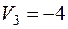
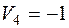
| 4 30 |  2 20 2 20
| 1 -2 | 3 1 | |
| 2 -3 | 3 10 | 4 20 | 1 20 | |

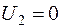
Примечание: в правом нижнем угле указаны относительные оценки небазисных клеток.
Если план не оптимален, то выбираем клетку с наименьшей отрицательной относительной оценкой и включаем эту клетку в базис, т.е. 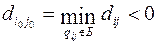
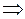
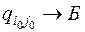 . (3)
. (3)
Чтобы найти клетку, исключаемую из базиса, строим цикл пересчёта, который начинается с клетки 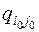 и в дальнейшем проходит по базисным клеткам. Циклом называется замкнутая ломаная линия, вершины которой расположены в базисных клетках, а звенья – вдоль строк и столбцов, причём в каждой строке и каждом столбце соединяются либо две клетки, либо не одной. Если ломаная цикла пересекается, то точки пересечения вершинами не являются.
и в дальнейшем проходит по базисным клеткам. Циклом называется замкнутая ломаная линия, вершины которой расположены в базисных клетках, а звенья – вдоль строк и столбцов, причём в каждой строке и каждом столбце соединяются либо две клетки, либо не одной. Если ломаная цикла пересекается, то точки пересечения вершинами не являются.
В клетках, расположенных в вершинах цикла перераспределяем объёмы перевозок. К клетке вводимой в базис добавляем некоторую величину Θ (промежуточная рента), из следующей клетки Θ вычитаем, далее прибавляем и т.д. Промежуточная рента Θ равна минимальному объёму перевозок в тех клетках, где Θ вычитаем. Базисная клетка, в которой объём перевозок равен Θ выходит из базиса (если таких клеток несколько, то выходит одна, а в других объёмы перевозок равны 0). Следующий план будет дешевле предыдущего на величину
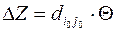 . (4)
. (4)
Произведем перераспределение перевозок и доведем до оптимального план из таблицы 13.
Выбираем наименьшую отрицательную относительную оценку (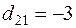 ) и эту клетку включаем в базис (
) и эту клетку включаем в базис (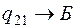 ).
).
В таблице 14 построен цикл пересчёта и перераспределены перевозки:
Таблица 14
4 30
 -Θ -Θ
|  2 20
+Θ 2 20
+Θ
| 1 | 3 | |
| 2 +Θ | 3 10 -Θ | 4 20 | 1 20 | |
Определим промежуточную ренту Θ:
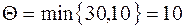
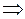
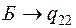 .
.
Уменьшение транспортных затрат: 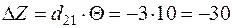 .
.
Новый план перевозок записан в таблице 15(изменяем объёмы перевозок только в клетках, находящихся в вершинах цикла):
Таблица 15
| 4 20 |  2 30 2 30
| 1 | 3 | |
| 2 10 | 3 | 4 20 | 1 20 | |
Проверим новый план на оптимальность.
Потенциалы строк и столбцов:
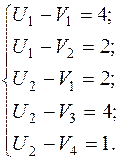
Пусть 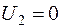 , тогда
, тогда 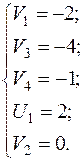
Относительные оценки:
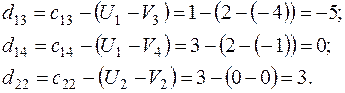
В таблице 16 представлен начальный план перевозок, проверенный на оптимальность:
Таблица 16
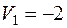
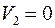
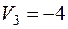
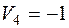
| 4 20 |  2 30 2 30
| 1 -5 | 3 0 | |
| 2 10 | 3 3 | 4 20 | 1 20 | |
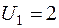
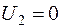
Т.к. есть 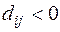 , текущий план не оптимален. Вводим клетку
, текущий план не оптимален. Вводим клетку 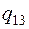 в базис и строим цикл пересчёта.
в базис и строим цикл пересчёта.
Новый план перевозок представлен в таблице 17.
Таблица 17
 4 20
-Θ 4 20
-Θ
|  2 30 2 30
| 1 +Θ | 3 | |
| 2 10 +Θ | 3 | 4 20 -Θ | 1 20 | |
Определим промежуточную ренту:
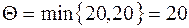
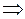
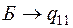 .
.
Уменьшение транспортных затрат: 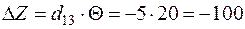 .
.
Новый план перевозок (смотри таблицу 18):
Таблица 18
| 4 |  2 30 2 30
| 1 20 | 3 | |
| 2 30 | 3 | 4 0 | 1 20 | |
Проверим новый план на оптимальность.
Потенциалы строк и столбцов:
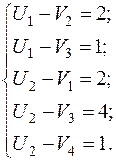 Пусть
Пусть 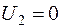 , тогда
, тогда 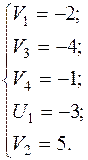
Относительные оценки:
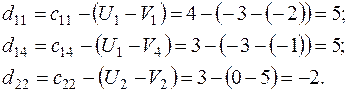
План перевозок имеет вид (смотри таблицу 19):
Таблица 19
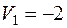
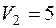
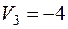
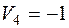
| 4 5 |  2 30 2 30
| 1 20 | 3 5 | |
| 2 30 | 3 -2 | 4 0 | 1 20 | |
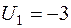
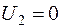
Т.к. есть 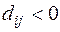 , текущий план не оптимален. Вводим клетку
, текущий план не оптимален. Вводим клетку 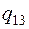 в базис и строим цикл пересчёта (смотри таблицу20).
в базис и строим цикл пересчёта (смотри таблицу20).
Таблица 20
| 4 |   2 30
-Θ 2 30
-Θ
| 1 20 +Θ | 3 | |
| 2 30 | 3 +Θ | 4 0 -Θ | 1 20 | |
Определим промежуточную ренту:
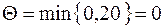
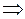
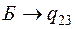 .
.
Уменьшение транспортных затрат: 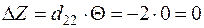 .
.
Новый план перевозок (смотри таблицу 21):
Таблица 21
| 4 |  2 30 2 30
| 1 20 | 3 | |
| 2 30 | 3 0 | 4 | 1 20 | |
Проверим новый план на оптимальность.
Потенциалы строк и столбцов:
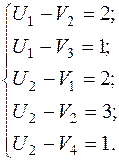 Пусть
Пусть 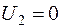 , тогда
, тогда 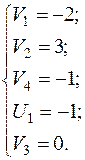
Относительные оценки:
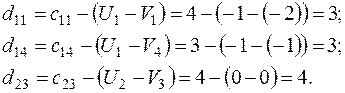
Т.к. нет 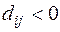 , текущий план оптимален.
, текущий план оптимален.
Стоимость перевозок по этому плану:
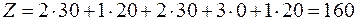 .
.
Минимальная стоимость перевозок в размере 160 руб. достигается, если перевезти с 1-го склада во 2-ой магазин 30 ед. товара и в 3-ий магазин 20 ед., а со 2-го склада – 30 ед. в 1-ый магазин и 20 ед. в 4-ый магазин.
|
|
|
|
|
Дата добавления: 2014-12-16; Просмотров: 685; Нарушение авторских прав?; Мы поможем в написании вашей работы!