Контрольная работа по дисциплине

«МЕТОДЫ ОПТИМАЛЬНЫХ РЕШЕНИЙ»

ВАРИАНТ 2

1. Дана задача линейного программирования

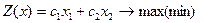
при ограничениях:

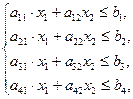
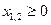
Графическим методом найти оптимальные решения при стремлении целевой функции к максимальному и минимальному значениям.

Значения коэффициентов целевой функции и системы ограничений

Значения	№ варианта
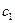
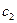
	-1
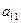
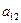
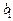
	-3
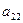
	-2
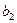
	-6
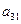
	-1

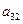
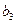
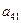
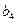
РЕШЕНИЕ:

Необходимо найти максимальное значение целевой функции F = 3x₁-x₂ → max, при системе ограничений:

5x1+2x2≤30	(1)
-3x1-2x2≤-6	(2)
-x1+x2≤0	(3)
x2≤5	(4)
x1≥0	(5)
x2≥0	(6)

Построим область допустимых решений, т.е. решим графически систему неравенств. Для этого построим каждую прямую и определим полуплоскости, заданные неравенствами (полуплоскости обозначены штрихом).

Построим уравнение 5x₁+2x₂ = 30 по двум точкам.

Для нахождения первой точки приравниваем x₁ = 0. Находим x₂ = 15. Для нахождения второй точки приравниваем x₂ = 0. Находим x₁ = 6. Соединяем точку (0;15) с (6;0) прямой линией. Определим полуплоскость, задаваемую неравенством. Выбрав точку (0; 0), определим знак неравенства в полуплоскости: 5 • 0 + 2 • 0 - 30 ≤ 0, т.е. 5x₁+2x₂ - 30≤ 0 в полуплоскости нижепрямой.

Построим уравнение -3x₁-2x₂ = -6 по двум точкам.

Для нахождения первой точки приравниваем x₁ = 0. Находим x₂ = 3. Для нахождения второй точки приравниваем x₂ = 0. Находим x₁ = 2. Соединяем точку (0;3) с (2;0) прямой линией. Определим полуплоскость, задаваемую неравенством. Выбрав точку (0; 0), определим знак неравенства в полуплоскости: -3 • 0 - 2 • 0 + 6 ≥ 0, т.е. -3x₁-2x₂ + 6≤ 0 в полуплоскости вышепрямой.

Построим уравнение -x₁+x₂ = 0 по двум точкам.

Для нахождения первой точки приравниваем x₁ = 1. Находим x₂ = 1. Для нахождения второй точки приравниваем x₂ = 1. Находим x₁ = 1. Соединяем точку (1;1) с (1;1) прямой линией. Определим полуплоскость, задаваемую неравенством. Выбрав точку (0; 0), определим знак неравенства в полуплоскости: -1 • 0 + 1 • 0 - 0 ≥ 0, т.е. -x₁+x₂ - 0≤ 0 в полуплоскости вышепрямой.

Построим уравнение x₂ = 5.

Эта прямая проходит через точку x₂ = 5 параллельно оси OX1. Определим полуплоскость, задаваемую неравенством. Выбрав точку (0; 0), определим знак неравенства в полуплоскости: 1 • 0 - 5 ≤ 0, т.е. x₂ - 5≤ 0 в полуплоскости ниже прямой.

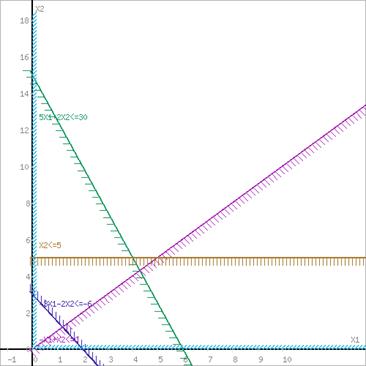
или

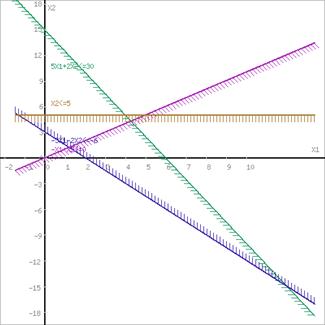
Границы области допустимых решений

Пересечением полуплоскостей будет являться область, координаты точек которого удовлетворяют условию неравенствам системы ограничений задачи.
Обозначим границы области многоугольника решений.

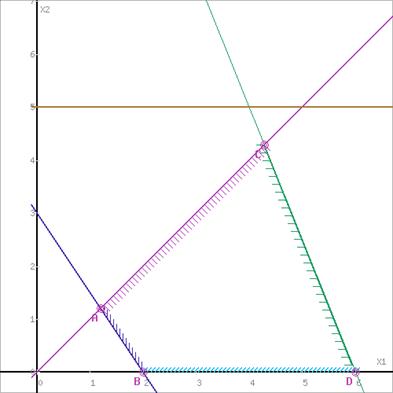
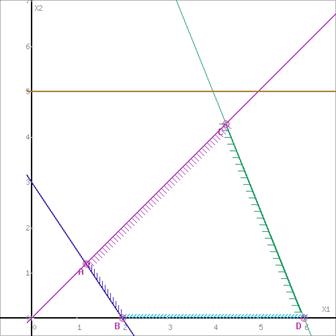
Рассмотрим целевую функцию задачи F = 3x₁-x₂ → max.
Построим прямую, отвечающую значению функции F = 0: F = 3x₁-x₂ = 0. Вектор-градиент, составленный из коэффициентов целевой функции, указывает направление максимизации F(X). Начало вектора – точка (0; 0), конец – точка (3; -1). Будем двигать эту прямую параллельным образом. Поскольку нас интересует максимальное решение, поэтому двигаем прямую до последнего касания обозначенной области. На графике эта прямая обозначена пунктирной линией.

Область допустимых решений представляет собой треугольник.

Прямая F(x) = const пересекает область в точке D. Так как точка D получена в результате пересечения прямых (5) и (1), то ее координаты удовлетворяют уравнениям этих прямых:
x₂=0
5x₁+2x₂=30
Решив систему уравнений, получим: x₁ = 6, x₂ = 0
Откуда найдем максимальное значение целевой функции:
F(X) = 3*6 - 1*0 = 18

Необходимо найти минимальное значение целевой функции F = 3x₁-x₂ → min, при системе ограничений:

5x1+2x2≤30	(1)
-3x1-2x2≤-6	(2)
-x1+x2≤0	(3)
x2≤5	(4)
x1≥0	(5)
x2≥0	(6)

Построим область допустимых решений, т.е. решим графически систему неравенств. Для этого построим каждую прямую и определим полуплоскости, заданные неравенствами (полуплоскости обозначены штрихом).
Построим уравнение 5x₁+2x₂ = 30 по двум точкам.
Для нахождения первой точки приравниваем x₁ = 0. Находим x₂ = 15. Для нахождения второй точки приравниваем x₂ = 0. Находим x₁ = 6. Соединяем точку (0;15) с (6;0) прямой линией. Определим полуплоскость, задаваемую неравенством. Выбрав точку (0; 0), определим знак неравенства в полуплоскости: 5 • 0 + 2 • 0 - 30 ≤ 0, т.е. 5x₁+2x₂ - 30≤ 0 в полуплоскости нижепрямой.
Построим уравнение -3x₁-2x₂ = -6 по двум точкам.
Для нахождения первой точки приравниваем x₁ = 0. Находим x₂ = 3. Для нахождения второй точки приравниваем x₂ = 0. Находим x₁ = 2. Соединяем точку (0;3) с (2;0) прямой линией. Определим полуплоскость, задаваемую неравенством. Выбрав точку (0; 0), определим знак неравенства в полуплоскости: -3 • 0 - 2 • 0 + 6 ≥ 0, т.е. -3x₁-2x₂ + 6≤ 0 в полуплоскости вышепрямой.
Построим уравнение -x₁+x₂ = 0 по двум точкам.
Для нахождения первой точки приравниваем x₁ = 1. Находим x₂ = 1. Для нахождения второй точки приравниваем x₂ = 1. Находим x₁ = 1. Соединяем точку (1;1) с (1;1) прямой линией. Определим полуплоскость, задаваемую неравенством. Выбрав точку (0; 0), определим знак неравенства в полуплоскости: -1 • 0 + 1 • 0 - 0 ≥ 0, т.е. -x₁+x₂ - 0≤ 0 в полуплоскости вышепрямой.
Построим уравнение x₂ = 5.
Эта прямая проходит через точку x₂ = 5 параллельно оси OX1. Определим полуплоскость, задаваемую неравенством. Выбрав точку (0; 0), определим знак неравенства в полуплоскости: 1 • 0 - 5 ≤ 0, т.е. x₂ - 5≤ 0 в полуплоскости ниже прямой.

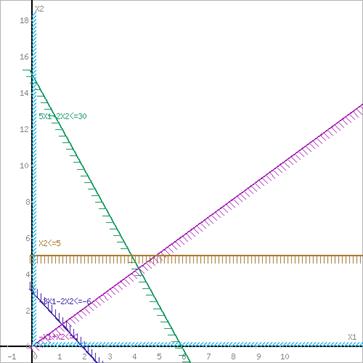
или

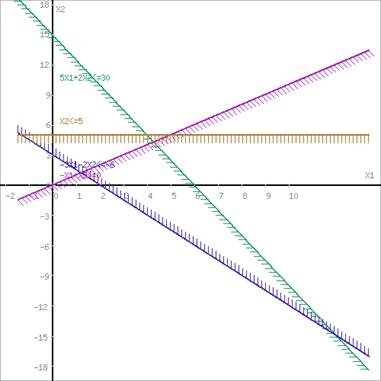
Границы области допустимых решений

Пересечением полуплоскостей будет являться область, координаты точек которого удовлетворяют условию неравенствам системы ограничений задачи.
Обозначим границы области многоугольника решений.

Рассмотрим целевую функцию задачи F = 3x₁-x₂ → min.
Построим прямую, отвечающую значению функции F = 0: F = 3x₁-x₂ = 0. Вектор-градиент, составленный из коэффициентов целевой функции, указывает направление минимизации F(X). Начало вектора – точка (0; 0), конец – точка (3; -1). Будем двигать эту прямую параллельным образом. Поскольку нас интересует минимальное решение, поэтому двигаем прямую до первого касания обозначенной области. На графике эта прямая обозначена пунктирной линией.

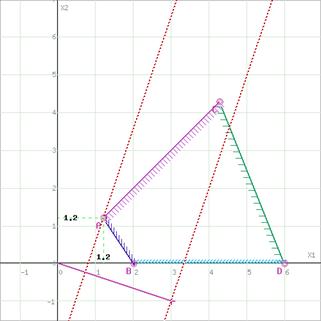
Область допустимых решений представляет собой треугольник.

Прямая F(x) = const пересекает область в точке A. Так как точка A получена в результате пересечения прямых (2) и (3), то ее координаты удовлетворяют уравнениям этих прямых:
-3x₁-2x₂=-6
-x₁+x₂=0
Решив систему уравнений, получим: x₁ = 1.2, x₂ = 1.2
Откуда найдем минимальное значение целевой функции:
F(X) = 3*1.2 - 1*1.2 = 2.4

2. Фирма изготовляет два вида красок для внутренних (В) и наружных (Н) работ. Для их производства используют исходные продукты: пигмент и олифу. Расходы исходных продуктов и максимальные суточные запасы указаны в таблице.

Расходы и суточные запасы исходных продуктов

Исходный продукт	Расход исходных продуктов на 1 т краски	Суточный запас, т
Краска Н	Краска В
Пигмент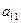
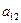
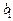
Олифа

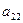
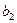
Изучение рынка сбыта показало, что суточный спрос на краску для наружных (внутренних) работ никогда не превышает 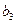т в сутки. Цена продажи 1 т краски для наружных работ 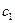ден. ед.

Какое количество краски каждого вида должна производить фирма, чтобы доход от реализации продукции был максимален?

Значения коэффициентов условий задачи

Значения	№ варианта
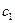
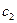
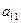
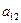
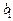
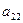
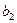
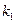
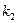
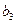
	2,5

РЕШЕНИЕ:

Необходимо найти максимальное значение целевой функции F = x₁+x₂ → max, при системе ограничений:

2x1+x2≤6	(1)
x1+2x2≤6	(2)
x1≤2.5	(3)
x1≥0	(4)
x2≥0	(5)

Построим область допустимых решений, т.е. решим графически систему неравенств. Для этого построим каждую прямую и определим полуплоскости, заданные неравенствами (полуплоскости обозначены штрихом).
Построим уравнение 2x₁+x₂ = 6 по двум точкам.
Для нахождения первой точки приравниваем x₁ = 0. Находим x₂ = 6. Для нахождения второй точки приравниваем x₂ = 0. Находим x₁ = 3. Соединяем точку (0;6) с (3;0) прямой линией. Определим полуплоскость, задаваемую неравенством. Выбрав точку (0; 0), определим знак неравенства в полуплоскости: 2 • 0 + 1 • 0 - 6 ≤ 0, т.е. 2x₁+x₂ - 6≤ 0 в полуплоскости нижепрямой.
Построим уравнение x₁+2x₂ = 6 по двум точкам.
Для нахождения первой точки приравниваем x₁ = 0. Находим x₂ = 3. Для нахождения второй точки приравниваем x₂ = 0. Находим x₁ = 6. Соединяем точку (0;3) с (6;0) прямой линией. Определим полуплоскость, задаваемую неравенством. Выбрав точку (0; 0), определим знак неравенства в полуплоскости: 1 • 0 + 2 • 0 - 6 ≤ 0, т.е. x₁+2x₂ - 6≤ 0 в полуплоскости нижепрямой.
Построим уравнение x₁ = 2.5.
Эта прямая проходит через точку x₁ = 2.5 параллельно оси OX2. Определим полуплоскость, задаваемую неравенством. Выбрав точку (0; 0), определим знак неравенства в полуплоскости: 1 • 0 - 2.5 ≤ 0, т.е. x₁ - 2.5≤ 0 в полуплоскости левее прямой.

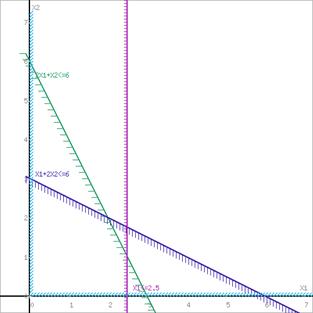
или

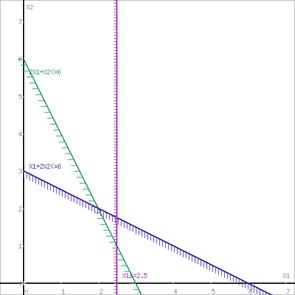
Границы области допустимых решений

Пересечением полуплоскостей будет являться область, координаты точек которого удовлетворяют условию неравенствам системы ограничений задачи.
Обозначим границы области многоугольника решений.

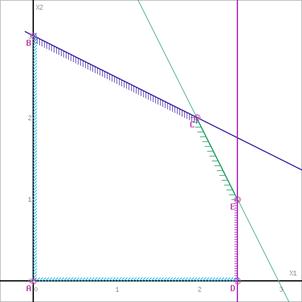
Рассмотрим целевую функцию задачи F = x₁+x₂ → max.
Построим прямую, отвечающую значению функции F = 0: F = x₁+x₂ = 0. Вектор-градиент, составленный из коэффициентов целевой функции, указывает направление максимизации F(X). Начало вектора – точка (0; 0), конец – точка (1; 1). Будем двигать эту прямую параллельным образом. Поскольку нас интересует максимальное решение, поэтому двигаем прямую до последнего касания обозначенной области. На графике эта прямая обозначена пунктирной линией.

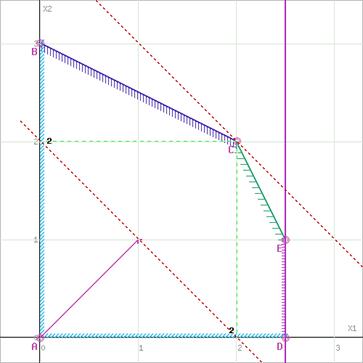
Область допустимых решений представляет собой многоугольник

Прямая F(x) = const пересекает область в точке C. Так как точка C получена в результате пересечения прямых (1) и (2), то ее координаты удовлетворяют уравнениям этих прямых:
2x₁+x₂=6
x₁+2x₂=6
Решив систему уравнений, получим: x₁ = 2, x₂ = 2
Откуда найдем максимальное значение целевой функции:
F(X) = 1*2 + 1*2 = 4

Дата добавления: 2014-12-16