Проверка опорного плана на оптимальность

Решить транспортную задачу, заданную распределительной таблицей.

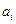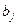
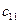
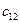
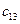
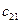
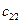
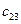
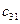
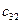
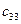
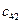
Значение коэффициентов распределительной таблицы.

Значения	№ варианта

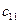
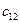
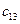
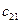
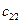
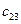
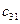
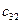
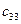
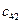
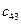
РЕШЕНИЕ:

Транспортная задача.

Стоимость доставки единицы груза из каждого пункта отправления в соответствующие пункты назначения задана матрицей тарифов

Распределительный метод является одним из вариантов базового симплексного метода. Поэтому идея распределительного метода (как и симплексного) содержит такие же три существенных момента.

Прежде всего отыскивается какое-то решение задачи — исходный опорный план. Затем посредством специальных показателей опорный план проверяется на оптимальность. Если план оказывается не оптимальным, переходят к другому плану. При этом второй и последующие планы должны быть лучше предыдущего. Так за несколько последовательных переходов от не оптимального плана приходят к оптимальному.

				Запасы
Потребности

Проверим необходимое и достаточное условие разрешимости задачи.

∑ a = 30 + 25 + 15 + 30 = 100

∑ b = 40 + 20 + 40 = 100

Условие баланса соблюдается. Запасы равны потребностям. Следовательно, модель транспортной задачи является закрытой.

Занесем исходные данные в распределительную таблицу.

				Запасы
Потребности

Первая итерация заключается в определении исходного опорного плана и проверке его на оптимальность.

Определение исходного опорного плана. Первый опорный план может быть найден посредством различных способов: по правилу северо-западного угла, приоритету ближайших пунктов, способу минимального элемента С=(cij), способу Фогеля и по способу Лебедева-Тихомирова.

Этап I. Поиск первого опорного плана.

1. Используя метод наименьшей стоимости, построим первый опорный план транспортной задачи.

Суть метода заключается в том, что из всей таблицы стоимостей выбирают наименьшую, и в клетку, которая ей соответствует, помещают меньшее из чисел a_i, или b_j.

Затем, из рассмотрения исключают либо строку, соответствующую поставщику, запасы которого полностью израсходованы, либо столбец, соответствующий потребителю, потребности которого полностью удовлетворены, либо и строку и столбец, если израсходованы запасы поставщика и удовлетворены потребности потребителя.

Из оставшейся части таблицы стоимостей снова выбирают наименьшую стоимость, и процесс распределения запасов продолжают, пока все запасы не будут распределены, а потребности удовлетворены.

Искомый элемент равен 1

Для этого элемента запасы равны 25, потребности 20. Поскольку минимальным является 20, то вычитаем его.

x₂₂ = min(25,20) = 20.

	x
			25 - 20 = 5
	x
	20 - 20 = 0

Искомый элемент равен 1

Для этого элемента запасы равны 30, потребности 40. Поскольку минимальным является 30, то вычитаем его.

x₄₁ = min(30,40) = 30.

	x
	x
		x	30 - 30 = 0
40 - 30 = 10

Искомый элемент равен 2

Для этого элемента запасы равны 5, потребности 10. Поскольку минимальным является 5, то вычитаем его.

x₂₁ = min(5,10) = 5.

	x
		x	5 - 5 = 0
	x
		x
10 - 5 = 5

Искомый элемент равен 3

Для этого элемента запасы равны 15, потребности 40. Поскольку минимальным является 15, то вычитаем его.

x₃₃ = min(15,40) = 15.

	x
		x
x	x		15 - 15 = 0
		x
		40 - 15 = 25

Искомый элемент равен 4

Для этого элемента запасы равны 30, потребности 25. Поскольку минимальным является 25, то вычитаем его.

x₁₃ = min(30,25) = 25.

	x		30 - 25 = 5
		x
x	x
		x
		25 - 25 = 0

Искомый элемент равен 6

Для этого элемента запасы равны 5, потребности 5. Поскольку минимальным является 5, то вычитаем его.

x₁₁ = min(5,5) = 5.

	x		5 - 5 = 0
		x
x	x
		x
5 - 5 = 0

				Запасы
	6[5]		4[25]
	2[5]	1[20]
			3[15]
	1[30]
Потребности

В результате получен первый опорный план, который является допустимым, так как все грузы из баз вывезены, потребность магазинов удовлетворена, а план соответствует системе ограничений транспортной задачи.

2. Подсчитаем число занятых клеток таблицы, их 6, а должно быть m + n - 1 = 6. Следовательно, опорный план является невырожденным.

Значение целевой функции для этого опорного плана равно:

F(x) = 6*5 + 4*25 + 2*5 + 1*20 + 3*15 + 1*30 = 235

Значение целевой функции для этого опорного плана равно:

6*5 + 4*25 + 2*5 + 1*20 + 3*15 + 1*30 = 235

Этап II. Улучшение опорного плана.

Шаг 1. Определяем оценку для каждой свободной клетки.

(1;2): В свободную клетку (1;2) поставим знак «+», а в остальных вершинах многоугольника чередующиеся знаки «-», «+», «-».

				Запасы
	6[5][-]	2[+]	4[25]
	2[5][+]	1[20][-]
			3[15]
	1[30]
Потребности

Цикл приведен в таблице (1,2 → 1,1 → 2,1 → 2,2).

Оценка свободной клетки равна Δ₁₂ = (2) - (6) + (2) - (1) = -3.

(2;3): В свободную клетку (2;3) поставим знак «+», а в остальных вершинах многоугольника чередующиеся знаки «-», «+», «-».

				Запасы
	6[5][+]		4[25][-]
	2[5][-]	1[20]	5[+]
			3[15]
	1[30]
Потребности

Цикл приведен в таблице (2,3 → 2,1 → 1,1 → 1,3).

Оценка свободной клетки равна Δ₂₃ = (5) - (2) + (6) - (4) = 5.

(3;1): В свободную клетку (3;1) поставим знак «+», а в остальных вершинах многоугольника чередующиеся знаки «-», «+», «-».

				Запасы
	6[5][-]		4[25][+]
	2[5]	1[20]
	5[+]		3[15][-]
	1[30]
Потребности

Цикл приведен в таблице (3,1 → 3,3 → 1,3 → 1,1).

Оценка свободной клетки равна Δ₃₁ = (5) - (3) + (4) - (6) = 0.

(3;2): В свободную клетку (3;2) поставим знак «+», а в остальных вершинах многоугольника чередующиеся знаки «-», «+», «-».

				Запасы
	6[5][-]		4[25][+]
	2[5][+]	1[20][-]
		6[+]	3[15][-]
	1[30]
Потребности

Цикл приведен в таблице (3,2 → 3,3 → 1,3 → 1,1 → 2,1 → 2,2).

Оценка свободной клетки равна Δ₃₂ = (6) - (3) + (4) - (6) + (2) - (1) = 2.

(4;2): В свободную клетку (4;2) поставим знак «+», а в остальных вершинах многоугольника чередующиеся знаки «-», «+», «-».

				Запасы
	6[5]		4[25]
	2[5][+]	1[20][-]
			3[15]
	1[30][-]	3[+]
Потребности

Цикл приведен в таблице (4,2 → 4,1 → 2,1 → 2,2).

Оценка свободной клетки равна Δ₄₂ = (3) - (1) + (2) - (1) = 3.

(4;3): В свободную клетку (4;3) поставим знак «+», а в остальных вершинах многоугольника чередующиеся знаки «-», «+», «-».

				Запасы
	6[5][+]		4[25][-]
	2[5]	1[20]
			3[15]
	1[30][-]		2[+]
Потребности

Цикл приведен в таблице (4,3 → 4,1 → 1,1 → 1,3).

Оценка свободной клетки равна Δ₄₃ = (2) - (1) + (6) - (4) = 3.

Опорный план является неоптимальным, поскольку имеются отрицательны оценки клеток (1,2;) равные: (-3).

Переход от неоптимального опорного плана к лучшему.

Поскольку в исходном опорном плане рассматриваемой задачи свободная клетка (1;2) имеет отрицательную оценку, то для получения плана, обеспечивающего меньшее значение целевой функции, эту клетку следует занять возможно большей поставкой, не нарушающей при этом условий допустимости плана.

Из грузов х_ij стоящих в минусовых клетках, выбираем наименьшее, т.е. у = min (1, 1) = 5. Прибавляем 5 к объемам грузов, стоящих в плюсовых клетках и вычитаем 5 из Х_ij, стоящих в минусовых клетках. В результате получим новый опорный план.

				Запасы
		2[5]	4[25]
	2[10]	1[15]
			3[15]
	1[30]
Потребности

2*5 + 4*25 + 2*10 + 1*15 + 3*15 + 1*30 = 220

Шаг 2. Определяем оценку для каждой свободной клетки.

(1;1): В свободную клетку (1;1) поставим знак «+», а в остальных вершинах многоугольника чередующиеся знаки «-», «+», «-».

				Запасы
	6[+]	2[5][-]	4[25]
	2[10][-]	1[15][+]
			3[15]
	1[30]
Потребности

Цикл приведен в таблице (1,1 → 1,2 → 2,2 → 2,1).

Оценка свободной клетки равна Δ₁₁ = (6) - (2) + (1) - (2) = 3.

(2;3): В свободную клетку (2;3) поставим знак «+», а в остальных вершинах многоугольника чередующиеся знаки «-», «+», «-».

				Запасы
		2[5][+]	4[25][-]
	2[10]	1[15][-]	5[+]
			3[15]
	1[30]
Потребности

Цикл приведен в таблице (2,3 → 2,2 → 1,2 → 1,3).

Оценка свободной клетки равна Δ₂₃ = (5) - (1) + (2) - (4) = 2.

(3;1): В свободную клетку (3;1) поставим знак «+», а в остальных вершинах многоугольника чередующиеся знаки «-», «+», «-».

				Запасы
		2[5][-]	4[25][+]
	2[10][-]	1[15][+]
	5[+]		3[15][-]
	1[30]
Потребности

Цикл приведен в таблице (3,1 → 3,3 → 1,3 → 1,2 → 2,2 → 2,1).

Оценка свободной клетки равна Δ₃₁ = (5) - (3) + (4) - (2) + (1) - (2) = 3.

(3;2): В свободную клетку (3;2) поставим знак «+», а в остальных вершинах многоугольника чередующиеся знаки «-», «+», «-».

				Запасы
		2[5][-]	4[25][+]
	2[10]	1[15]
		6[+]	3[15][-]
	1[30]
Потребности

Цикл приведен в таблице (3,2 → 3,3 → 1,3 → 1,2).

Оценка свободной клетки равна Δ₃₂ = (6) - (3) + (4) - (2) = 5.

(4;2): В свободную клетку (4;2) поставим знак «+», а в остальных вершинах многоугольника чередующиеся знаки «-», «+», «-».

				Запасы
		2[5]	4[25]
	2[10][+]	1[15][-]
			3[15]
	1[30][-]	3[+]
Потребности

Цикл приведен в таблице (4,2 → 4,1 → 2,1 → 2,2).

Оценка свободной клетки равна Δ₄₂ = (3) - (1) + (2) - (1) = 3.

(4;3): В свободную клетку (4;3) поставим знак «+», а в остальных вершинах многоугольника чередующиеся знаки «-», «+», «-».

				Запасы
		2[5][+]	4[25][-]
	2[10][+]	1[15][-]
			3[15]
	1[30][-]		2[+]
Потребности

Цикл приведен в таблице (4,3 → 4,1 → 2,1 → 2,2 → 1,2 → 1,3).

Оценка свободной клетки равна Δ₄₃ = (2) - (1) + (2) - (1) + (2) - (4) = 0.

Из приведенного расчета видно, что ни одна свободная клетка не имеет отрицательной оценки, следовательно, дальнейшее снижение целевой функции Fx невозможно, поскольку она достигла минимального значения.

Таким образом, последний опорный план является оптимальным.

Минимальные затраты составят:

2*5 + 4*25 + 2*10 + 1*15 + 3*15 + 1*30 = 220

Если в оптимальном решении задачи имеется несколько оценок равных нулю, то это является свидетельством того, что среди бесчисленного множества решений этой задачи существуют еще решения, являющиеся также оптимальными, поскольку значение целевой функции остается одинаковым — минимальным. Их принято называть альтернативными.

Анализ оптимального плана.

Из 1-го склада необходимо груз направить в 2-й магазин (5), в 3-й магазин (25)

Из 2-го склада необходимо груз направить в 1-й магазин (10), в 2-й магазин (15)

Из 3-го склада необходимо весь груз направить в 3-й магазин

Из 4-го склада необходимо весь груз направить в 1-й магазин

5. Решить транспортную задачу. Заданы мощности поставщиков а_j (j = 1, 2, 3), емкости потребителей b_j (j = 1, 2, 3) и матрица стоимостей перевозок единицы продукции от каждого поставщика каждому потребителю. Требуется найти план перевозок, при котором суммарные транспортные затраты будут наименьшими.

 

b_j

5.2.

аj

РЕШЕНИЕ:

Математическая модель транспортной задачи:

F = ∑∑c_ijx_ij, (1)

при условиях:

∑x_ij = a_i, i = 1,2,…, m, (2)

∑x_ij = b_j, j = 1,2,…, n, (3)

x_ij ≥ 0

Запишем экономико-математическую модель для нашей задачи.

Переменные:

x₁₁ – количество груза из 1-го склада в 1-й магазин

x₁₂ – количество груза из 1-го склада в 2-й магазин

x₁₃ – количество груза из 1-го склада в 3-й магазин

x₂₁ – количество груза из 2-го склада в 1-й магазин

x₂₂ – количество груза из 2-го склада в 2-й магазин

x₂₃ – количество груза из 2-го склада в 3-й магазин

x₃₁ – количество груза из 3-го склада в 1-й магазин

x₃₂ – количество груза из 3-го склада в 2-й магазин

x₃₃ – количество груза из 3-го склада в 3-й магазин

Ограничения по запасам:

x₁₁ + x₁₂ + x₁₃ ≤ 17

x₂₁ + x₂₂ + x₂₃ ≤ 30

x₃₁ + x₃₂ + x₃₃ ≤ 15

Ограничения по потребностям:

x₁₁ + x₂₁ + x₃₁ ≥ 40

x₁₂ + x₂₂ + x₃₂ ≥ 12

x₁₃ + x₂₃ + x₃₃ ≥ 20

Целевая функция:

8x₁₁ + 4x₁₂ + 9x₁₃ + 6x₂₁ + 3x₂₂ + 7x₂₃ + 5x₃₁ + 2x₃₂ + 4x₃₃ → min

С целью составления двойственной задачи переменные x_ij в условии (2) заменим на u₁, u₂, u_i,.., u_m, а переменные x_ij в условия (3) на v₁, v₂, v_j,.., v_n.

Поскольку каждая переменная x_ij входит в условия (2,3) и целевую функцию (1) по одному разу, то двойственную задачу по отношению к прямой транспортной задаче можно сформулировать следующим образом.

Требуется найти не отрицательные числа u_i (при i = 1,2,…,m) и v_j (при j = 1,2,..,n), обращающие в максимум целевую функцию

G = ∑a_iu_i + ∑b_jv_j

при условии

u_i + v_j ≤ c_ij, i = 1,2,..,m; j = 1,2,..,n (4)

В систему условий (4) будет mxn неравенств. По теории двойственности для оптимальных планов прямой и двойственной задачи для всех i,j должно быть:

u_i + v_j ≤ c_ij, если x_ij = 0,

u_i + v_j = c_ij, если x_ij ≥ 0,

Эти условия являются необходимыми и достаточными признаками оптимальности плана транспортной задачи.

Числа u_i, v_j называются потенциалами. Причем число u_i называется потенциалом поставщика, а число v_j – потенциалом потребителя.

По первой теореме двойственности в оптимальном решении значения целевых функций прямой и двойственных задач совпадают: F = G.

Стоимость доставки единицы груза из каждого пункта отправления в соответствующие пункты назначения задана матрицей тарифов

				Запасы
Потребности

Проверим необходимое и достаточное условие разрешимости задачи.

∑a = 17 + 30 + 15 = 62

∑b = 40 + 12 + 20 = 72

Как видно, суммарная потребность груза в пунктах назначения меньше запасов груза на базах. Следовательно, модель исходной транспортной задачи является открытой. Чтобы получить закрытую модель, введем дополнительную (фиктивную) потребность, равной 10 (72—62). Тарифы перевозки единицы груза из базы во все магазины полагаем равны нулю.

Занесем исходные данные в распределительную таблицу.

				Запасы
Потребности

Этап I. Поиск первого опорного плана.

1. Используя метод наименьшей стоимости, построим первый опорный план транспортной задачи.

Суть метода заключается в том, что из всей таблицы стоимостей выбирают наименьшую, и в клетку, которая ей соответствует, помещают меньшее из чисел a_i, или b_j.

Затем, из рассмотрения исключают либо строку, соответствующую поставщику, запасы которого полностью израсходованы, либо столбец, соответствующий потребителю, потребности которого полностью удовлетворены, либо и строку и столбец, если израсходованы запасы поставщика и удовлетворены потребности потребителя.

Из оставшейся части таблицы стоимостей снова выбирают наименьшую стоимость, и процесс распределения запасов продолжают, пока все запасы не будут распределены, а потребности удовлетворены.

Искомый элемент равен 2

Для этого элемента запасы равны 15, потребности 12. Поскольку минимальным является 12, то вычитаем его.

x₃₂ = min(15,12) = 12.

	x
	x
			15 - 12 = 3
	12 - 12 = 0

Искомый элемент равен 4

Для этого элемента запасы равны 3, потребности 20. Поскольку минимальным является 3, то вычитаем его.

x₃₃ = min(3,20) = 3.

	x
	x
x			3 - 3 = 0
		20 - 3 = 17

Искомый элемент равен 6

Для этого элемента запасы равны 30, потребности 40. Поскольку минимальным является 30, то вычитаем его.

x₂₁ = min(30,40) = 30.

	x
	x	x	30 - 30 = 0
x
40 - 30 = 10

Искомый элемент равен 8

Для этого элемента запасы равны 17, потребности 10. Поскольку минимальным является 10, то вычитаем его.

x₁₁ = min(17,10) = 10.

	x		17 - 10 = 7
	x	x
x
10 - 10 = 0

Искомый элемент равен 9

Для этого элемента запасы равны 7, потребности 17. Поскольку минимальным является 7, то вычитаем его.

x₁₃ = min(7,17) = 7.

	x		7 - 7 = 0
	x	x
x
		17 - 7 = 10

Искомый элемент равен 0

Для этого элемента запасы равны 10, потребности 10. Поскольку минимальным является 10, то вычитаем его.

x₄₃ = min(10,10) = 10.

	x
	x	x
x
			10 - 10 = 0
		10 - 10 = 0

				Запасы
	8[10]		9[7]
	6[30]
		2[12]	4[3]
			0[10]
Потребности

В результате получен первый опорный план, который является допустимым, так как все грузы из баз вывезены, потребность магазинов удовлетворена, а план соответствует системе ограничений транспортной задачи.

2. Подсчитаем число занятых клеток таблицы, их 6, а должно быть m + n - 1 = 6. Следовательно, опорный план является невырожденным.

Значение целевой функции для этого опорного плана равно:

F(x) = 8*10 + 9*7 + 6*30 + 2*12 + 4*3 + 0*10 = 359

Этап II. Улучшение опорного плана.

Проверим оптимальность опорного плана. Найдем предварительные потенциалы u_i, v_j. по занятым клеткам таблицы, в которых u_i + v_j = c_ij, полагая, что u₁ = 0.

u₁ + v₁ = 8; 0 + v₁ = 8; v₁ = 8

u₂ + v₁ = 6; 8 + u₂ = 6; u₂ = -2

u₁ + v₃ = 9; 0 + v₃ = 9; v₃ = 9

u₃ + v₃ = 4; 9 + u₃ = 4; u₃ = -5

u₃ + v₂ = 2; -5 + v₂ = 2; v₂ = 7

u₄ + v₃ = 0; 9 + u₄ = 0; u₄ = -9

	v1=8	v2=7	v3=9
u1=0	8[10]		9[7]
u2=-2	6[30]
u3=-5		2[12]	4[3]
u4=-9			0[10]

Опорный план не является оптимальным, так как существуют оценки свободных клеток, для которых u_i + v_j > c_ij

(1;2): 0 + 7 > 4; ∆₁₂ = 0 + 7 - 4 = 3

(2;2): -2 + 7 > 3; ∆₂₂ = -2 + 7 - 3 = 2

max(3,2) = 3

Выбираем максимальную оценку свободной клетки (1;2): 4

Для этого в перспективную клетку (1;2) поставим знак «+», а в остальных вершинах многоугольника чередующиеся знаки «-», «+», «-».

				Запасы
	8[10]	4[+]	9[7][-]
	6[30]
		2[12][-]	4[3][+]
			0[10]
Потребности

Цикл приведен в таблице (1,2 → 1,3 → 3,3 → 3,2).

Из грузов х_ij стоящих в минусовых клетках, выбираем наименьшее, т.е. у = min (1, 3) = 7. Прибавляем 7 к объемам грузов, стоящих в плюсовых клетках и вычитаем 7 из Х_ij, стоящих в минусовых клетках. В результате получим новый опорный план.

				Запасы
	8[10]	4[7]
	6[30]
		2[5]	4[10]
			0[10]
Потребности

Проверим оптимальность опорного плана. Найдем предварительные потенциалы u_i, v_j. по занятым клеткам таблицы, в которых u_i + v_j = c_ij, полагая, что u₁ = 0.

u₁ + v₁ = 8; 0 + v₁ = 8; v₁ = 8

u₂ + v₁ = 6; 8 + u₂ = 6; u₂ = -2

u₁ + v₂ = 4; 0 + v₂ = 4; v₂ = 4

u₃ + v₂ = 2; 4 + u₃ = 2; u₃ = -2

u₃ + v₃ = 4; -2 + v₃ = 4; v₃ = 6

u₄ + v₃ = 0; 6 + u₄ = 0; u₄ = -6

	v1=8	v2=4	v3=6
u1=0	8[10]	4[7]
u2=-2	6[30]
u3=-2		2[5]	4[10]
u4=-6			0[10]

Опорный план не является оптимальным, так как существуют оценки свободных клеток, для которых u_i + v_j > c_ij

(3;1): -2 + 8 > 5; ∆₃₁ = -2 + 8 - 5 = 1

(4;1): -6 + 8 > 0; ∆₄₁ = -6 + 8 - 0 = 2

max(1,2) = 2

Выбираем максимальную оценку свободной клетки (4;1): 0

Для этого в перспективную клетку (4;1) поставим знак «+», а в остальных вершинах многоугольника чередующиеся знаки «-», «+», «-».

				Запасы
	8[10][-]	4[7][+]
	6[30]
		2[5][-]	4[10][+]
	0[+]		0[10][-]
Потребности

Цикл приведен в таблице (4,1 → 4,3 → 3,3 → 3,2 → 1,2 → 1,1).

Из грузов х_ij стоящих в минусовых клетках, выбираем наименьшее, т.е. у = min (3, 2) = 5. Прибавляем 5 к объемам грузов, стоящих в плюсовых клетках и вычитаем 5 из Х_ij, стоящих в минусовых клетках. В результате получим новый опорный план.

				Запасы
	8[5]	4[12]
	6[30]
			4[15]
	0[5]		0[5]
Потребности

Проверим оптимальность опорного плана. Найдем предварительные потенциалы u_i, v_j. по занятым клеткам таблицы, в которых u_i + v_j = c_ij, полагая, что u₁ = 0.

u₁ + v₁ = 8; 0 + v₁ = 8; v₁ = 8

u₂ + v₁ = 6; 8 + u₂ = 6; u₂ = -2

u₄ + v₁ = 0; 8 + u₄ = 0; u₄ = -8

u₄ + v₃ = 0; -8 + v₃ = 0; v₃ = 8

u₃ + v₃ = 4; 8 + u₃ = 4; u₃ = -4

u₁ + v₂ = 4; 0 + v₂ = 4; v₂ = 4

	v1=8	v2=4	v3=8
u1=0	8[5]	4[12]
u2=-2	6[30]
u3=-4			4[15]
u4=-8	0[5]		0[5]

Опорный план является оптимальным, так все оценки свободных клеток удовлетворяют условию u_i + v_j ≤ c_ij.

Минимальные затраты составят:

F(x) = 8*5 + 4*12 + 6*30 + 4*15 + 0*5 + 0*5 = 328

Проверим оптимальность найденного плана по первой теореме двойственности (в оптимальном решении значения целевых функций прямой и двойственных задач совпадают: F = G).

G = 0•17 -2•30 -4•15 -8•10 + 8•40 + 4•12 + 8•20 = 328

Анализ оптимального плана.

Из 1-го склада необходимо груз направить в 1-й магазин (5), в 2-й магазин (12)

Из 2-го склада необходимо весь груз направить в 1-й магазин

Из 3-го склада необходимо весь груз направить в 3-й магазин

Потребность 1-го магазина остается неудовлетворенной на 5 ед.

Оптимальный план является вырожденным, так как базисная переменная x₄₁=0.

Потребность 3-го магазина остается неудовлетворенной на 5 ед.

Оптимальный план является вырожденным, так как базисная переменная x₄₃=0.

Дата добавления: 2014-12-16