
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Составить математическую модель и решить задачу симплексным методом
|
|
|
|
В производстве пользующихся спросом двух изделий, А или В, принимают участие 3 цеха. На изготовление одного изделия А первый цех затрачивает  час, второй цех -
час, второй цех - 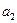 час, третий цех -
час, третий цех -  час. На изготовление одного изделия В первый цех затрачивает
час. На изготовление одного изделия В первый цех затрачивает 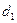 час, второй цех -
час, второй цех -  час, третий цех -
час, третий цех - 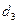 час. На производство обоих изделий первый цех может затратить не более
час. На производство обоих изделий первый цех может затратить не более 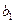 час, второй цех не более
час, второй цех не более 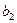 час, третий цех – не более
час, третий цех – не более 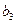 час.
час.
От реализации одного изделия А фирма получает доход 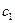 руб., изделие В -
руб., изделие В - 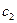 руб.
руб.
Определить максимальный доход от реализации всех изделий А и В.
Значение коэффициентов условия задачи
| Значения | № варианта | |

| ||

| ||

| ||
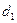
| ||

| ||
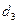
| ||
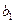
| ||
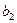
| ||
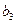
| ||
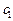
| ||
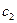
|
РЕШЕНИЕ:
Математическая модель
10х1 + 18 х2 ≤ 1238
9х1+ 15х2 ≤ 1118
3х1 + х2 ≤ 523
Для постановки задачи на максимум целевую функцию запишем так:
11х1 + 13 х2→ max
Решим прямую задачу линейного программирования симплексным методом, с использованием симплексной таблицы.
Определим максимальное значение целевой функции F(X) = 11x1 + 13x2 при следующих условиях-ограничений.
10x1 + 18x2≤1238
9x1 + 15x2≤1118
3x1 + x2≤523
Для построения первого опорного плана систему неравенств приведем к системе уравнений путем введения дополнительных переменных (переход к канонической форме).
В 1-м неравенстве смысла (≤) вводим базисную переменную x3. В 2-м неравенстве смысла (≤) вводим базисную переменную x4. В 3-м неравенстве смысла (≤) вводим базисную переменную x5.
10x1 + 18x2 + 1x3 + 0x4 + 0x5 = 1238
9x1 + 15x2 + 0x3 + 1x4 + 0x5 = 1118
3x1 + 1x2 + 0x3 + 0x4 + 1x5 = 523
Матрица коэффициентов A = a(ij) этой системы уравнений имеет вид:
Базисные переменные это переменные, которые входят только в одно уравнение системы ограничений и притом с единичным коэффициентом.
Экономический смысл дополнительных переменных: дополнительные переменные задачи ЛП обозначают излишки сырья, времени, других ресурсов, остающихся в производстве данного оптимального плана.
Решим систему уравнений относительно базисных переменных: x3, x4, x5
Полагая, что свободные переменные равны 0, получим первый опорный план:
X1 = (0,0,1238,1118,523)
Базисное решение называется допустимым, если оно неотрицательно.
| Базис | B | x1 | x2 | x3 | x4 | x5 |
| x3 | ||||||
| x4 | ||||||
| x5 | ||||||
| F(X0) | -11 | -13 |
Переходим к основному алгоритму симплекс-метода.
1. Проверка критерия оптимальности.
Текущий опорный план неоптимален, так как в индексной строке находятся отрицательные коэффициенты.
2. Определение новой базисной переменной.
В качестве ведущего выберем столбец, соответствующий переменной x2, так как это наибольший коэффициент по модулю.
3. Определение новой свободной переменной.
Вычислим значения Di по строкам как частное от деления: bi / ai2
и из них выберем наименьшее:
min (1238: 18, 1118: 15, 523: 1) = 687/9
Следовательно, 1-ая строка является ведущей.
Разрешающий элемент равен (18) и находится на пересечении ведущего столбца и ведущей строки.
| Базис | B | x1 | x2 | x3 | x4 | x5 | min |
| x3 | 687/9 | ||||||
| x4 | 748/15 | ||||||
| x5 | |||||||
| F(X1) | -11 | -13 |
4. Пересчет симплекс-таблицы.
Формируем следующую часть симплексной таблицы.
Вместо переменной x3 в план 1 войдет переменная x2.
Строка, соответствующая переменной x2 в плане 1, получена в результате деления всех элементов строки x3 плана 0 на разрешающий элемент РЭ=18
На месте разрешающего элемента в плане 1 получаем 1.
В остальных клетках столбца x2 плана 1 записываем нули.
Таким образом, в новом плане 1 заполнены строка x2 и столбец x2.
Все остальные элементы нового плана 1, включая элементы индексной строки, определяются по правилу прямоугольника.
Для этого выбираем из старого плана четыре числа, которые расположены в вершинах прямоугольника и всегда включают разрешающий элемент РЭ.
НЭ = СЭ - (А*В)/РЭ
СТЭ - элемент старого плана, РЭ - разрешающий элемент (18), А и В - элементы старого плана, образующие прямоугольник с элементами СТЭ и РЭ.
Представим расчет каждого элемента в виде таблицы:
| B | x 1 | x 2 | x 3 | x 4 | x 5 |
| 1238: 18 | 10: 18 | 18: 18 | 1: 18 | 0: 18 | 0: 18 |
| 1118-(1238 • 15):18 | 9-(10 • 15):18 | 15-(18 • 15):18 | 0-(1 • 15):18 | 1-(0 • 15):18 | 0-(0 • 15):18 |
| 523-(1238 • 1):18 | 3-(10 • 1):18 | 1-(18 • 1):18 | 0-(1 • 1):18 | 0-(0 • 1):18 | 1-(0 • 1):18 |
| 0-(1238 • -13):18 | -11-(10 • -13):18 | -13-(18 • -13):18 | 0-(1 • -13):18 | 0-(0 • -13):18 | 0-(0 • -13):18 |
Получаем новую симплекс-таблицу:
| Базис | B | x1 | x2 | x3 | x4 | x5 |
| x2 | 619/9 | 5/9 | 1/18 | |||
| x4 | 259/3 | 2/3 | -5/6 | |||
| x5 | 4088/9 | 22/9 | -1/18 | |||
| F(X1) | 8047/9 | -34/9 | 13/18 |
1. Проверка критерия оптимальности.
Текущий опорный план неоптимален, так как в индексной строке находятся отрицательные коэффициенты.
2. Определение новой базисной переменной.
В качестве ведущего выберем столбец, соответствующий переменной x1, так как это наибольший коэффициент по модулю.
3. Определение новой свободной переменной.
Вычислим значения Di по строкам как частное от деления: bi / ai1
и из них выберем наименьшее:
min (687/9: 5/9, 861/3: 2/3, 4542/9: 24/9) = 1234/5
Следовательно, 1-ая строка является ведущей.
Разрешающий элемент равен (5/9) и находится на пересечении ведущего столбца и ведущей строки.
| Базис | B | x1 | x2 | x3 | x4 | x5 | min |
| x2 | 687/9 | 5/9 | 1/18 | 1234/5 | |||
| x4 | 861/3 | 2/3 | -5/6 | 1291/2 | |||
| x5 | 4542/9 | 24/9 | -1/18 | 1859/11 | |||
| F(X2) | 8941/9 | -37/9 | 13/18 |
4. Пересчет симплекс-таблицы.
Формируем следующую часть симплексной таблицы.
Вместо переменной x2 в план 2 войдет переменная x1.
Строка, соответствующая переменной x1 в плане 2, получена в результате деления всех элементов строки x2 плана 1 на разрешающий элемент РЭ=5/9
На месте разрешающего элемента в плане 2 получаем 1.
В остальных клетках столбца x1 плана 2 записываем нули.
Таким образом, в новом плане 2 заполнены строка x1 и столбец x1.
Все остальные элементы нового плана 2, включая элементы индексной строки, определяются по правилу прямоугольника.
Представим расчет каждого элемента в виде таблицы:
| B | x 1 | x 2 | x 3 | x 4 | x 5 |
| 687/9: 5/9 | 5/9: 5/9 | 1: 5/9 | 1/18: 5/9 | 0: 5/9 | 0: 5/9 |
| 861/3-(687/9 • 2/3):5/9 | 2/3-(5/9 • 2/3):5/9 | 0-(1 • 2/3):5/9 | -5/6-(1/18 • 2/3):5/9 | 1-(0 • 2/3):5/9 | 0-(0 • 2/3):5/9 |
| 4542/9-(687/9 • 24/9):5/9 | 24/9-(5/9 • 24/9):5/9 | 0-(1 • 24/9):5/9 | -1/18-(1/18 • 24/9):5/9 | 0-(0 • 24/9):5/9 | 1-(0 • 24/9):5/9 |
| 8941/9-(687/9 • -37/9):5/9 | -37/9-(5/9 • -37/9):5/9 | 0-(1 • -37/9):5/9 | 13/18-(1/18 • -37/9):5/9 | 0-(0 • -37/9):5/9 | 0-(0 • -37/9):5/9 |
Получаем новую симплекс-таблицу:
| Базис | B | x1 | x2 | x3 | x4 | x5 |
| x1 | 619/5 | 9/5 | 1/10 | |||
| x4 | 19/5 | -6/5 | -9/10 | |||
| x5 | 758/5 | -22/5 | -3/10 | |||
| F(X2) | 6809/5 | 34/5 | 11/10 |
1. Проверка критерия оптимальности.
Среди значений индексной строки нет отрицательных. Поэтому эта таблица определяет оптимальный план задачи.
Окончательный вариант симплекс-таблицы:
| Базис | B | x1 | x2 | x3 | x4 | x5 |
| x1 | 619/5 | 9/5 | 1/10 | |||
| x4 | 19/5 | -6/5 | -9/10 | |||
| x5 | 758/5 | -22/5 | -3/10 | |||
| F(X3) | 6809/5 | 34/5 | 11/10 |
Оптимальный план можно записать так:
x1 = 1234/5
F(X) = 11•1234/5 = 13614/5
Анализ оптимального плана.
В оптимальный план вошла дополнительная переменная x4. Следовательно, при реализации такого плана имеются недоиспользованные ресурсы 2-го вида в количестве 34/5
В оптимальный план вошла дополнительная переменная x5. Следовательно, при реализации такого плана имеются недоиспользованные ресурсы 3-го вида в количестве 1513/5
Значение 0 в столбце x1 означает, что использование x1 - выгодно.
Значение 64/5> 0 в столбце x2 означает, что использование x2 - не выгодно.
Значение 11/10 в столбце x3 означает, что теневая цена (двойственная оценка) равна 11/10.
|
|
|
|
|
Дата добавления: 2014-12-16; Просмотров: 2516; Нарушение авторских прав?; Мы поможем в написании вашей работы!