Численные методы и обработка данных

Матричные операции линейной алгебры

Операторы и функции

Некоторые специальные символы:

a (:, j) – j-й столбец матрицы a;

a (i,:) – i-я строка матрицы a;

a (j: k) – элементы a _j, a _j+1, …, a _k;

a (:) – записывает все элементы массива a в виде столбца;

a (m,:) =[ ] – удаляет из матрицы строку m;

a ’ – транспонированная матрица а;

a. ’ – транспонирование массива;

prod(a) – произведение элементов массива;

prod(a, dim) – произведение элементов столбцов (dim=1) или строк (dim=2);

sum(a) – сумма элементов массива;

sum(a, dim) - сумма элементов столбцов (dim=1) или строк (dim=2).

· det(a) – возвращает определитель квадратной матрицы а;

· rank(a) – возвращает ранг матрицы;

· norm(a) – возвращает норму матрицы а;

· b=orth(a) – возвращает ортонормальный базис матрицы а;

· inv(a) – возвращает матрицу, обратную матрице а;

· spec(a) – возвращает вектор собственных значений матрицы а.

Примеры:

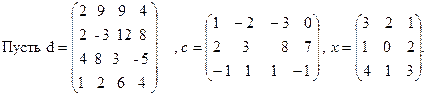
Вычислить: определитель матрицы d; ранг матрицы c; обратную матрицу к матрице x.

Решение:

В командном окне в строках ввода набираем:

--> d=[2 9 9 4; 2 -3 12 8; 4 8 3 -5; 1 2 6 4];

--> c=[1, -2, -3, 0; 2, 3, 8, 7; -1, 1, 1, -1];

-->x=[3 2 1; 1 0 2; 4 1 3];

--> x1=det(d), x2=rank(c), x3=inv(x)

В строках вывода получаем:

x1 =

147.

x2 =

2.

x3 =

-0.4 -1. 0.8

1. 1. -1.

0.2 1. -0.4

Решение систем линейных уравнений

Пример: решить систему линейных уравнений

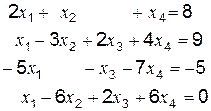
Решение возможно одним из способов (s₁, s₂, s₃ или s₄ – см. приведенную ниже программу).

--> a=[2, 1, 0, 1; 1, -3, 2, 4; -5, 0, -1, -7; 1, -6, 2, 6]; b=[8 9 -5 0];

--> s1=b/a', s2=a\b', s3=b*a'^(-1), s4=b*inv(a')

s1 =

8.1481481 - 1.5185185 11.703704 - 6.7777778

s2 =

8.1481481

- 1.5185185

11.703704

- 6.7777778

s3 =

8.1481481 - 1.5185185 11.703704 - 6.7777778

s4 =

8.1481481 - 1.5185185 11.703704 - 6.7777778

Решить систему линейных уравнений вида 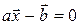можно с помощью функции linsolve: linsolve(a,b). В нашем примере:

a=[2, 1, 0, 1; 1, -3, 2, 4; -5, 0, -1, -7; 1, -6, 2, 6]; b=[8; 9;-5;0]; x=linsolve(a,b)

x =

- 8.1481481

1.5185185

- 11.703704

6.7777778

Если система уравнений имеет бесчисленное множество решений, то выводится одно из них:

a=[2, 1; 4, 2]; b=[-7; -14 ];x=linsolve(a,b)

x =

2.8

1.4

Если система не имеет решений:

a=[2, 1; 4, 2]; b=[-7; -13 ];x=linsolve(a,b)

WARNING:Conflicting linear constraints!

x =

[]

Вычисление корней полинома

Функция roots(c) возвращает вектор-столбец из корней полинома с.

Пример: решить уравнение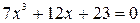

--> x=[7, 0, 12, 23]; d=roots(x)

d =

0.5564046 + 1.6257442i

0.5564046 - 1.6257442i

- 1.1128093

Примечание: Коэффициенты полинома следует вводить в порядке убывания степеней переменной x. Если в уравнении отсутствует слагаемое, содержащее, например, x², то в векторе коэффициентов на соответствующем месте надо ввести 0.

Решение нелинейных уравнений вида f(x)=0

Уравнения бывают алгебраическими и трансцендентными. Алгебраическим называют уравнение вида 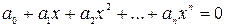. Если уравнение нельзя свести к алгебраическому заменой переменных, то его называют трансцендентным. Пример:

Для решения уравнений, в том числе трансцендентных, в Scilab применяют функцию fsolve(x0,f)

где x0 - начальное приближение, f - функция, описывающая левую часть уравнения f(x)=0.

Пример: решить уравнение

Набираем в окне редактора файл:

function y=f (x)

y= 7 *x. ^3+45 *x. ^2 + 12 *x+ 23;

endfunction

и сохраняем его под именем f.sci. Загружаем его в Scilab (Execute/Load into Scilab).

Для нахождения отрезка [ a, b], на котором отделен корень данного уравнения, построим график функции .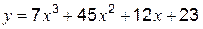

-->x=-8:0.1:-5; plot(x, f(x)); xgrid()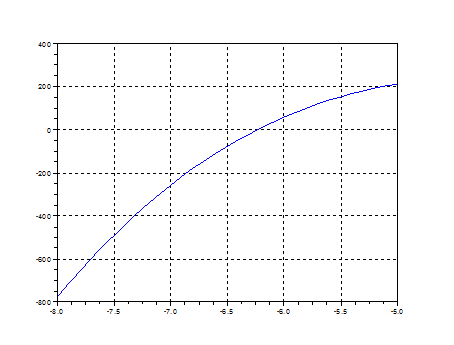

Из графика видно, что корень отделен на отрезке [-6.5, -6]. Найдем его, используя функцию fsolve:

-->x0=-6.5;x1= fsolve(x0,f)

Получаем:

x1 =

- 6.2381997

Систему нелинейных уравнений также можно решить, используя функцию fsolve.

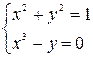
clc

function [y]=ff(x)

y(1)=x(1)^2+x(2)^2-1;

y(2)=x(1)^3-x(2);

endfunction

t=fsolve([-.5,-.5],ff)

t =

- 0.8260314 - 0.5636242

Поиск минимума функции y=f(x) на интервале [ a, b]

Функция [f,xopt]=optim(costf,x0) возвращает локальный минимум функции costf.

Функция возвращает минимум функции (значение f) и точку, в которой этот минимум достигается (xopt).

Главной особенностью функции optim является структура функции costf, которая должна быть такой:

function [f,g,ind]=costf(x,ind)

f=gg(x);//функция, минимум которой мы ищем

g=numdiff(gg,x); //градиент функции f

Дата добавления: 2014-12-17