Способ 2

Способ 1.

Численное интегрирование

При вычислении определенных интегралов от функций, заданных в виде таблицы или в явном виде (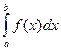), одним из численных методов используют функции intsplin, inttrap, integrate, intg.

С помощью команды intsplin. Это интегрирование экспериментальных данных с помощью сплайн-интерполяции. Известно значение интегрируемой функции в дискретных точках (узлах).

Пример: вычислить интеграл от таблично заданной функции

x		1.4	1.8	2.2	2.6		3.4	3.8	4.2	4.6
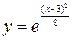
	1.6487	1.3771	1.1972	1.0833	1.0202		1.0202	1.0833	1.1972	1.3771	1.6487

-->x=1:.4:5;

-->y=exp((x-3).^2/8)//значения у в таблице получены табулированием этой функции

-->v=intsplin(x,y)

Получаем:

v =

4.7799684

Или:

-->x=[1 1.4 1.8 2.2 2.6 3 3.4 3.8 4.2 4.6 5];

-->y=[1.6487 1.3771 1.1972 1.0833 1.0202 1 1.0202 1.0833 1.1972 1.3771 1.6487];

-->v=intsplin(x,y)

v =

4.7799328

С помощью команды inttrap. Интегрирование экспериментальных данных с помощью трапецеидальной интерполяции (метод трапеций).

При вычислении интеграла между соседними узлами функция интерполируется линейно. Этот метод вычислений называется методом трапеций.

Вычислим интеграл от той же самой функции

-->x=1:.4:5;

-->y=exp((x-3).^2/8)

-->v=inttrap(x,y)

Получаем:

v =

4.8017553

Способ 3. С помощью команды integrate. Это интегрирование по квадратуре. Может задаваться требуемая точность вычислений.

Синтаксис [x]=integrate(expr,v,x0,x1 [,ea [,er]])

Параметры

expr: подынтегральная функция;

v: переменная интегрирования;

x0, x1: пределы интегрирования;

ea, er: действительные числа. Первое из них – еа - предельная абсолютная ошибка. По умолчанию принимает значение 0. Второе - er -, - предельная относительная ошибка. По умолчанию принимает значение 1.d-8.

Пример: вычислить .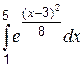

-->integrate('exp((x-3)^2/8)','x',1,5)

ans =

4.7798306

Можно это сделать и так.

Набираем и сохраняем в окне редактора под именем a.sci файл

function g=a(x)

g=exp((x-3).^2/8);

endfunction

Загружаем этот файл в среду Scilab (Load into Scilab).

Далее в строке ввода набираем:

-->integrate('a','x',1,5)

Получаем:

ans =

4.7798306

Дата добавления: 2014-12-17