Момент силы относительно центра (или точки)

Опыт показывает, что под действием силы твердое тело может наряду с поступательным перемещением совершать вращение вокруг того или иного центра. Вращательный эффект силы характеризуется ее момен­том

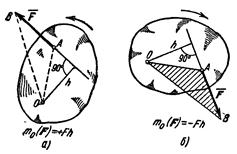
Рассмотрим силуF, приложенную в точке А твердого тела (рис. 15). Допустим, что сила стремится повернуть тело вокруг центра О. Перпендикуляр h, опущенный из центра O на линию действия силы F, на­зывается плечом силы F от­носительно центра О. Так как точку приложения силы можно произвольно переме­щать вдоль линии действия, то, очевидно, вращательный эффект силы будет зависеть: 1) от модуля силы F и длины плеча h; 2) от поло­жения плоскости поворота ОАВ, проходящей через центр О и силуF; 3) от направления поворота к этой плоскости.

Ограничимся пока рассмотрением систем сил, лежащих в одной плоскости. В этом случае

плоскость поворота для всех сил является общей и в дополнительном задании не нуждается. Рис. 15.

Тогда для количественного измерения вращательного эффекта можно ввести следующее понятие о моменте силы: моментом силы F относительно центра О называется величина, равная взятому с соответствующим знаком произведению модуля силы на длину плеча.

Момент силы F относительно центра О будем обозначать сим­волом m₀(F). Следовательно,

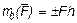
В дальнейшем условимся считать, что момент имеет знак плюс, если сила стремится повернуть тело вокруг центра О против хода ча­совой стрелки, и знак минус, - если по ходу часовой стрелки. Так, для силыF, изображенной на рис. 15, а, момент относительно центра О имеет знак плюс, а для силы, показанной на рис. 15, б, - знак ми­нус.

Отметим следующие свойства момента силы:

1) Момент силы не изменяется при переносе точки приложения силы вдольее линии действия.

2) Момент силы относительно центра О равен нулю только тогда, когда сила равна нулю или когда линия действия силы проходит через центр О (плечо равно нулю).

3) Момент силы численно выражается удвоенной площадью тре­угольника ОАВ (рис. 15, б)

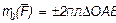
Этот результат следует из того, что

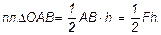
Теорема Вариньона о моменте равнодействующей.

Докажем следующую теорему Вариньона: момент равнодействующей плоской системы сходящихся сил от­носительно любого центра равен алгеб­раической сумме моментов слагаемых сил относительно того же центра.

Рассмотрим систему силF₁, F₂, … F_n, сходящихся в точке А (рис. 16). Возьмем произвольный центр О и проведем через него ось Ох, перпендикулярную к прямой ОА; положительное направление оси Ох выбираем так, чтобы знак проекции любой из сил на эту ось совпадал со знаком ее момента относительно центра О.

Рис. 16.

Для доказательства теоремы найдем соответствующие выражения моментов m₀(F₁), m₀(F₂), …. По формуле 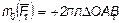. Но, как видно из рисунка, , где F_1x - проекция силы F₁ на ось Ох; сле­довательно

.

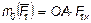Аналогично вычисляются моменты всех других сил.

Обозначим равнодействующую сил F₁, F₂, … F_n,черезR, где 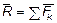. Тогда, по теореме о проекции суммы сил на ось, получим . Умножая обе части этого равенства на ОА, найдем:

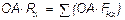
или,

.

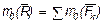Пара сил. Момент пары.

Парой сил называется система двух равных по модулю, параллельных и направленных в противо­положные стороны сил, действующих на абсолютно твердое тело (рис. 17). Система сил, образующих пару, очевидно, не находится в равновесии (см. аксиому 1).

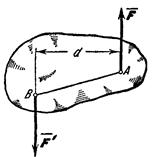Плоскость, проходящая через линии действия сил пары, назы­вается плоскостью действия пары. Расстояние d между линиями действия сил пары называется плечом пары. Действие пары сил на твердое тело сводится к некоторому вращательному эффекту, завися­щему от: 1) модуля F сил пары и длины ее плеча d; 2) положения плоскости действия пары; 3) направления поворота в этой плоскости. Для характеристики этого эффекта вводится понятие момента пары.

Пo аналогии с моментом силы введем следующее определение: моментом пары называется величина, равная взятому с соответствующим знаком, произведению модуля одной из сил пары на ее плечо. Будем обозначать момент пары буквой т или М. Тогда

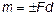Рис. 17.

Момент пары (как и момент силы) будем считать положи­тельным, когда пара стремится повернуть тело против хода часовой стрелки, и отрицательным - когда по ходу часовой стрелки. Из рис. 17 видно, что момент пары равен моменту одной из ее сил относительно точки приложения другой,

т. е.

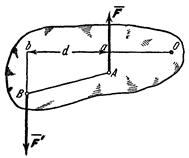Докажем следующую теорему о моментах сил пары: алгебраическая сумма моментов сил пары, относительно любого центра, лежа­щего в плоскости ее действия, не зависит от выбора этого центра и равна моменту пары. В самом деле, беря в плоскости действия пары любую точку О (рис. 18), находим: 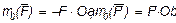. Складывая, эти равенства почленно и замечая, что F' = F и

Ob — Oa = d, где d—плечо пары, полу­чаем: Рис. 18.

Доказанной теоремой удобно пользо­ваться при вычислении моментов сил пары относительно любого центра.

Дата добавления: 2014-12-17