Законы трения скольжения

Изучение данных вопросов необходимо в дальнейшем для изучения динамики движении тел с учетом трения скольжения и трения качения, динамики движения центра масс механической системы, кинетических моментов, для решения задач в дисциплине «Сопротивление материалов».

МОДУЛЬ 2

ЛЕКЦИЯ 3

Модуль 2 состоит из 2-ух лекций в которых изучаются следующие вопросы:

1. Равновесие системы тел.

2. Расчет ферм.

3. Понятие о ферме.

4. Аналитический расчет плоских ферм.

5. Графический расчет плоских ферм.

6. Трение.

7. Законы трения скольжения.

8. Реакции шероховатых связей.

9. Угол трения.

10. Равновесие при наличии трения.

11. Трение качения и верчения.

12. Момент силы относительно центра как вектор.

13. Момент пары сил как вектор.

14. Момент силы относительно оси.

15. Зависимость между моментами силы относительно центра и относительно оси.

16. Приведение пространственной системы сил к данному центру.

17. Условия равновесия произвольной пространственной системы сил.

18. Задачи на равновесие тела под действием пространственной системы сил.

19. Центр тяжести твердого тела.

20. Координаты центров тяжести однородных тел.

21. Центры тяжести некоторых однородных тел.

Равновесие систем тел.

Статический расчет инженерных со­оружений во многих случаях сводится к рассмотрению условий равно­весия конструкции из системы тел, соединенных какими - нибудь свя­зями. Связи, соединяющие части данной конструкции, будем называть внутренними, в отличие от внешних связей, скрепляющих конструк­цию с телами, в нее не входящими (например, с опорами).

Если после отбрасывания внешних связей (опор) конструкция остается жесткой, то для нее задачи статики решаются как для аб­солютно твердого тела.

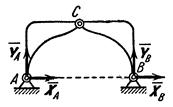
Однако могут встречаться такие инженерные конструкции, кото­рые после отбрасывания внешних связей не остаются жесткими. При­мером такой конструкции является трехшарнирная арка (рис. 22). Если отбросить опоры А и В, то арка не будет жесткой: ее части могут поворачиваться вокруг шар­нира С. Рис. 22.

На основании принципа отвердевания система сил, действующих на такую кон­струкцию, должна при равновесии удов­летворять условиям равновесия твердого тела. Но эти условия, как указывалось, будучи необходимыми, не будут являться достаточными, поэтому из них нельзя будет определить всех неизвестных. Для решения задачи необходимо будет дополнительно рассмотреть равновесие какой-ни­будь одной или нескольких частей конструкции.

Например, составляя условия равновесия для сил, действующих на трех шарнирную арку (см. рис. 22), мы получим три уравнения с четырьмя неизвестными X_A, Y_A, X_B, Y_B. Рассмотрев дополнительно условия равновесия левой (или правой) ее половины, мы получим еще три уравнения, содержащие два новых неизвестных Х_C, Y_C, на рис. 22 не показанных. Решая полученную систему шести уравнений, найдем все шесть неизвестных.

Другой способ решения подобных задач состоит в том, что кон­струкцию сразу расчленяют на отдельные тела и составляют усло­вия равновесия каждого из тел, рассматривая его как свободное. При этом реакции внутренних связей будут попарно равны по модулю и противоположны по направлению. Для конструк­ции из п тел, на каждое из которых действует произвольная плоская си­стема сил, получится таким путем 3n уравнений, позволяющих найти Зn неизвестных (при других системах сил число уравнений соответственно изменится). Если для данной конструк­ции число всех реакций связей будет больше числа уравнений, в которые эти реакции входят, то конструкция будет статически неопределимой.

РАСЧЕТ ФЕРМ

Понятие о ферме. Аналитический расчет плоских ферм.

Фермой называется жесткая конструкция из прямолинейных стержней, соединенных на концах шарнирами. Если все стержни фермы лежат в одной плоскости, ферма называется плоской. Места соединения стержней фермы называют узлами. Все внешние нагрузки к ферме прикладываются только в узлах. При расчете фермы трением в узлах и весом стержней (по сравнению с внешними нагрузками) пренебрегают или распределяют веса стержней по узлам. Тогда на каждый из стержней фермы будут действовать две силы, приложен­ные к его концам, которые при равновесии могут быть направлены только вдоль стержня. Следовательно, можно считать, что стержни фермы работают только на растяжение или на сжатие. Огра­ничимся рассмотрением жестких плоских ферм, без лишних стержней, образованных из треугольников. В таких фермах число стержней k и число узлов п связаны соотношением

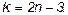
Расчет фермы сводится к определению опорных реакций и уси­лий в ее стержнях.

Опорные реакции можно найти обычными методами статики, рассматривая ферму в целом как твердое тело. Перейдем к определе­нию усилий в стержнях.

Метод вырезания узлов. Этим методом удобно пользоваться, когда надо найти усилия во всех стержнях фермы. Он сводится к по­следовательному рассмотрению условий равновесия сил, сходящихся в каждом из узлов фермы. Ход расчетов поясним на конкретном примере.

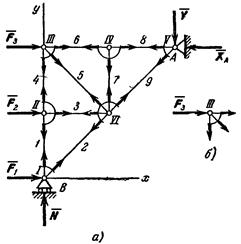Рассмотрим изображенную на рис. 2З,а ферму, образованную из одинаковых равнобедренных прямоугольных треугольников; действую­щие на ферму силы парал­лельны оси х и равны: F₁ = F₂ = F₃ = F = 2.

В этой ферме число узлов n = 6, а число стержней k = 9. Следовательно, соот­ношение выполняется и ферма является жесткой, без лишних стержней.

Составляя уравнения рав­новесия для фермы в целом, найдем, что реакции опор направлены, как пока­зано на рисунке, и численно равны;

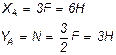
Переходим к определению усилий в стержнях. Рис. 23.

Пронумеруем узлы фермы римскими цифрами, а стержни — арабскими. Искомые усилия будем обозначать S₁ (в стержне 1), S₂ (в стержне 2) и т. д. Отрежем мысленно все узлы вместе со сходящимися в них стержнями от осталь­ной фермы. Действие отброшенных частей стержней заменим силами, которые будут направлены вдоль соответствующих стержней и численно равны искомым усилиям S₁, S₂,... Изображаем сразу все эти силы на рисунке, направляя их от узлов, т. е. считая, все стержни растя­нутыми (рис. 23, а; изображенную картину надо представлять себе для каждого узла так, как это показано на рис. 23, б для узла III). Если в результате расчета величина усилия в каком-нибудь стержне получится отрицательной, это будет означать, что данный стержень не растянут, а сжат. Буквенных обозначений для сил, действующих вдоль стержней, ни рис. 2З не вводам, поскольку ясно, что силы, действующие вдоль стержня 1, равны численно S₁, вдоль стержня 2 — равны S₂ и т. д.

Теперь для сил, сходящихся в каждом узле, составляем последо­вательно уравнения равновесия

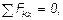
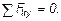
Начинаем с узла 1, где сходятся два стержня, так как из двух уравнений равновесия можно определить только два неизвестных усилия.

Составляя уравнения равновесия для узла 1, получим

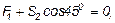
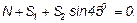
Отсюда находим

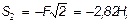
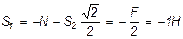
Теперь, зная S₁, переходим к узлу II. Для него уравнения равнове­сия дают

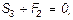
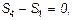
откуда

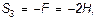
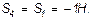
Определив S₄, составляем аналогичным путем уравнения равновесия сначала для узла III, а затем для узла IV. Из этих уравнений находим:

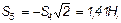
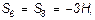
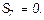
Наконец, для вычисления S₉ составляем уравнение равновесия сил, сходящихся в узле V, проектируя их на ось By. Получим 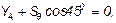откуда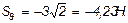

Второе уравнение равновесия для узла V и два уравнения для узла VI можно составить как поверочные. Для нахождения усилий в стержнях эти уравнения не понадобились, так как вместо них были использованы три уравнения равновесия всей фермы в целом при определении N, Х_А, и Y_А.

Окончательные результаты расчета можно свести в таблицу:

№ стержня..........	1	2	3	4	5	6	7	8	9
Усилие в Н.........	-1	-2,82	-2	-1	+1,41	-3	0	-3	-4,23

Как показывают знаки усилий, стержень 5 растянут, остальные стер­жни сжаты; стержень 7 не нагружен (нулевой, стержень).

Наличие в ферме нулевых стержней, подобных стержню 7, обна­руживается сразу, так как если в узле, не нагруженном внешними силами, сходятся три стержня, из которых два направлены вдоль одной прямой, то усилие в третьем стержне равно нулю. Этот результат получается из уравнения равновесия в проекции на ось, перпендикулярную к упомянутым двум стержням.

Если в ходе расчета встретится узел, для которого число неизве­стных больше двух, то можно воспользоваться методом сечений.

Метод сечений (метод Риттера). Этим методом удобно поль­зоваться для определения усилий в отдельных стержнях фермы, в ча­стности, для проверочных расчетов. Идея метода состоит в том, что ферму разделяют на две части сечением, проходящим через три стержня, в которых (или в одном из которых) требуется определить усилие, и рассматривают равновесие одной из этих частей. Действие отброшенной части заменяют соответствующими силами, направляя их вдоль разрезанных стержней от узлов, т. е. считая стержни рас­тянутыми (как и в методе вырезания узлов). Затем составляют урав­нения равновесия, беря центры моментов (или ось проекций) так, чтобы в каждое уравнение вошло только одно неизвестное усилие.

Графический расчет плоских ферм.

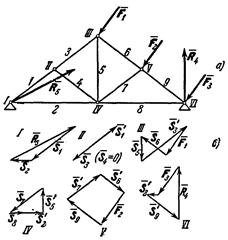Расчет фермы мето­дом вырезания узлов может производиться графически. Для этого сначала, определяют опорные реакции. Затем, последовательно отсекая от фермы каждый из ее узлов, нахо­дят усилия в стержнях, сходящихся в этих узлах, строя соответствую­щие замкнутые силовые многоугольники. Все построения проводятся в масштабе, который должен быть заранее выбран. Рас­чет начинают с узла, в котором сходятся два стержня (иначе не удастся определить неизвест­ные усилия).

В качестве примера рас­смотрим ферму, изображен­ную на рис. 24, а. В этой ферме число узлов n = 6, а число стержней k = 9. Следовательно, соотношение выполняется и ферма является жесткой, без лиш­них стержней. Опорные реак­цииR₄ и R₅ для рассматри­ваемой фермы, изображаем на­ряду с силами F₁, F₂ и F₃, как известные.

Определение усилий в стержнях начинаем с рас­смотрения стержней, сходя­щихся в узле I (узлы нуме­руем римскими цифрами, а стержни - арабскими). Мысленно отрезав от этих стержней остальную часть фермы, отбрасываем ее Рис. 24.

действие отброшенной части также мысленно заменяем силами

S₁ и S₂, которые должны быть направлены вдоль

стержней 1 и 2. Из сходящихся в узле I сил R₅, S₁ и S₂ строим замкнутый треугольник (рис. 24, б). Для этого изображаем сначала в выбранном масштабе известную силу R₅, а затем проводим через ее начало и конец прямые, параллельные стерж­ням 1 и 2. Таким путем будут найдены силы S₁ и S₂, действующие на стержни 1 и 2. Затем рассматриваем равновесие стержней, сходящихся в узле II. Действие на эти стержни отброшенной части фермы мысленно заменяем силами S₁’, S₂, и S₄, направленными вдоль соответствующих стержней; при этом сила S₁ нам известна, так как по равенству дей­ствия и противодействия S₁’ = -S₁. Построив из сил, сходящихся в узле II, замкнутый треугольник (начиная с силы S₁’), найдем вели­чины S₃ и S₄ (в данном случае S₄ = =0). Аналогично находятся усилия в остальных стержнях. Соответствующие силовые многоугольники для всех узлов показаны на рис. 24, б. Последний много­угольник (для узла VI) строится для про­верки, так как все входящие в него силы уже найдены.

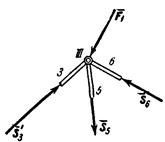
Из построенных многоугольников, зная масштаб, находим величины всех усилий. Знак усилия в каждом стержне опреде­ляется следующим образом. Мысленно вы­резав узел по сходящимся в нем стержням (например, узел III), прикладываем к обрезам стержней найденные силы (рис. 25); сила, направленная от узла (S₅ на рис. 25), растягивает стержень,

а си­ла, направленная к узлу (S₃’ и S₆ на рис. 25) сжимает

его. Рис. 25.

Соглас­но принятому условию растягивающим усилиям приписываем знак «+», а сжимающим - знак «-». В рассмотренном примере

(pиc. 25) стержни 1, 2, 3, 6, 7, 9 сжаты, а стержни 5, 8 растянуты.

ТРЕНИЕ

Опыт показывает, что при стремлении двигать одно тело по поверхности другого в плоскости соприкосновения тел возникает сила сопротивления их относительному скольжению, называемая силой трения скольжения.

Возникновение трения обусловлено, прежде всего, шероховатостью поверхностей, создающей сопротивление перемещению, и наличием сцепления у прижатых друг к другу тел. Изучение всех особенностей явления трения представляет собою довольно сложную физико-меха­ническую проблему, рассмотрение которой выходит за рамки курса теоретической механики.

В инженерных расчетах обычно исходят из ряда установленных опытным путем общих закономерностей, которые с достаточной для практики точностью отражают основные особенности явления трения. Эти закономерности, называемые законами трения скольжения при покое, можно сформулировать следующим образом:

1. При стремлении сдвинуть одно тело по поверхности другого в плоскости соприкосновения тел возникает сила трения(или сила сцепления), величина которой может принимать любые значения от нуля до значения F_пр, называемого предельной силой трения.

Сила трения направлена в сторону, противоположную той, куда действующие силы стремятся сдвинуть тело.

2. Величина предельной силы трения равна произведению стати­ческого коэффициента трения на нормальное давление или нормаль­ную реакцию:

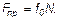
Статический коэффициент трения f₀ — число отвлеченное; он опре­деляется опытным путем и зависит от материала соприкасающихся тел и состояния поверхностей (характер обработки, температура, влажность, смазка и т. п.).

3. Величина предельной силы трения в довольно широких пределах не зависит от размеров соприкасающихся при трении поверхностей.

Объединяя вместе первый и второй законы, получаем, что при равновесии сила трения покоя (сила сцепления) F ≤ F_пр или

Дата добавления: 2014-12-17