Момент силы относительно центра как вектор

Чтобы перейти к решению задач статики для системы сил, как угодно расположенных в пространстве, оказывается необходимым несколько уточнить и расширить ряд введенных ранее понятий. Начнем с понятия о моменте силы.

1. Изображение момента вектором. Момент силы F относительно центра О (см. рис. 29) как характеристика ее враща­тельного эффекта определяется следую­щими тремя элементами:

1) модулем мо­мента, равным произведению модуля силы на плечо, т. е. Fh; 2) плоскостью поворота ОАВ, проходящей через линию действия силы F и центр О; 3) напра­влением поворота в этой плоскости. Когда все силы и центр О лежат в одной пло­скости, необходимость задавать каждый раз плоскость Рис. 29.

поворота ОАВ отпадает, и момент можно определять как скаляр­ную алгебраическую величину, равную ±Fh, где знак указывает направление поворота.

Но в случае сил, произвольно расположенных в пространстве, плоскости поворота у разных сил будут разными и должны задаваться дополнительно. Положение плоскости в пространстве можно задать, задав отрезок (вектор), перпендикулярный к этой плоскости. Если одновременно модуль этого вектора выбрать равным модулю момента силы и условиться направлять этот вектор так, чтобы его направление определяло направление поворота силы, то такой вектор полностью определит все три элемента, характеризующие момент данной силы относительно центра О.

Поэтому в общем случае момент m_o(F) силы F относительно центра О (рис. 29) будем изображать приложенным в центре О вектором М_о, равным по модулю (в выбранном масштабе) произ­ведению модуля силы F на плечо h и перпендикулярным к пло­скости ОАВ, проходящей через центр О и силу F. Направлять вектор М_о будем в ту сторону, откуда поворот, совершаемый силой, виден происходящим против хода часовой стрелки. Таким образом, вектор М_о будет одновременно характеризовать модуль момента, плоскость поворота ОАВ, разную для разных сил, и направление поворота в этой плоскости. Точка приложения вектора М_о определяет положение центра момента.

2. Выражение момента силы с помощью вектор­ного произведения. Рассмотрим векторное произведение ОА x F векторов ОА и F (рис. 29). По определению,

,

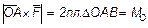так как модуль вектора М_о тоже равен 2 пл. ∆ ОАВ. Направлен вектор (ОА x F) перпендикулярно к плоскости ОАВ, в ту сторону, откуда кратчайшее совмещение ОА с F (если их отложить от одной точки) видно против хода часовой стрелки, т. е., так же, как век­тор М_о. Следовательно, векторы (ОА x F) и М_о совпадают и по модулю и по направлению и, как легко проверить, по размерности, т. е. оба эти вектора изображают одну и ту же величину. Отсюда

или ,

где вектор r = ОА называется радиусом-вектором точки А относи­тельно центра О.

Таким образом, момент силы F относительно центра О равен векторному произведению радиуса вектора r = ОА, соединяющего центр О с точкой приложения силы А, на саму силу. Этим вы­ражением момента силы бывает удобно пользоваться при доказатель­стве некоторых теорем.

Дата добавления: 2014-12-17