Момент пары сил как вектор

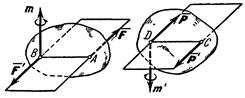Действие пары сил на тело характеризуется: 1) величиной модуля момента пары, 2) плоскостью действия, 3) направлением поворота в этой плоскости. При рассмот­рении пар, не лежащих в одной плоскости, для характеристики каж­дой из пар необходимо бу­дет задать все эти три эле­мента. Это можно сделать, если условиться, по аналогии с моментом силы, изображать момент пары соответствую­щим образом, построенным вектором, а именно: будем изображать момент пары вектором т илиМ, мо­дуль которого равен (в выбранном масштабе) модулю момента пары, Рис. 30.

т. е. произведению одной из ее сил на плечо, и который направлен перпендикулярно плоскости действия пары в ту сто­рону, откуда поворот пары виден происходящим против хода часовой стрелки (рис. 30).

Как известно модуль момента пары равен моменту одной из ее сил относительно точки, где приложена другая сила, т. е. m = m_B(F); по направлению же векторы этих моментов совпадают. Следовательно

.

Момент силы относительно оси.

Чтобы перейти к решению задач статики для случая произвольной пространственной системы сил, необходимо ввести еще понятие о моменте силы относительно оси.

Момент силы относительно оси характеризует вращательный эффект, создаваемый силой, стремящейся повернуть тело вокруг дан­ной оси. Рассмотрим твердое тело, которое может вращаться вокруг некоторой оси z (рис. 31). Пусть на это тело действует силаF,приложенная в точке А. Проведем через точку А плоскость ху, пер­пендикулярную оси z, и разложим силу F на составляющие: F_z, параллельную осиz, и F_xy, лежа­щую в плоскости ху (F_xy является одновременно проекцией силы F на плоскости ху). Сила F_z, на­правленная параллельно оси z, очевидно, Рис. 31.

не может повернуть тело вокруг этой оси (она только стре­мится сдвинуть тело вдоль оси z). Весь вращательный эффект, создаваемый силойF, будет совпадать с вращательным эффек­том ее составляющей F_xy. Отсюда заключаем, что

,

где символ m_xy(F) обозначает момент силы F относительно оси z.

Для силы же F_xy, лежащей в плоскости, перпендикулярной к оси z, вращательный эффект измеряется произведением модуля этой силы на ее расстояние h от оси. Но этой же величиной измеряется момент силы F_xy относительно точки О, в которой ось z пересекается с пло­скостью xу. Следовательно или, согласно преды­дущему равенству,

.

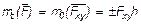В результате приходим к следующему определению: моментом силы относительно оси называется скалярная величина, равная моменту проекции этой силы на плоскость, перпендикулярную оси, взятому относительно точки пересечения оси с плоскостью.

Момент будем считать положительным, если с положительного конца оси z поворот, который сила F_xy, стремится совершить, виден происходящим против хода часовой стрелки, и отрицательным, если по ходу часовой стрелки.

Из чертежа (рис. 32) видно, что при вычислении момента плоскость ху можно проводить через любую точку оcи z. Таким образом, чтобы найти момент силы относительно оси z (рис. 32) надо: 1) провести плоскость ху, перпендикулярную к оси z (в любом месте);

2) спроектировать Рис. 32.

силу F на эту плоскость и вычислить вели­чину F_xy; 3) опустить

из точки О пересечения оси с плоскостью перпендикуляр на направ­ление F_xy и найти его длину h; 4) вычислить произведение F_xyh; 5) определить знак момента.

При вычислении моментов надо иметь в виду следующие частные случаи:

1) Если сила параллельна оси, то ее момент относительно оси равен нулю (так как F_xy = 0).

2) Если линия действия силы пересекает ось, то ее момент отно­сительно оси также равен нулю (так как h = 0).

Объединяя оба случая вместе, заключаем, что момент силы от­носительно оси равен нулю, если сила и ось лежат в одной плоскости.

3) Если сила перпенди­кулярна к оси, то ее момент относительно оси равен про­изведению модуля силы на расстояние между силой и осью.

Дата добавления: 2014-12-17