Задачи на равновесие тела под действием пространст­венной системы сил

Условия равновесия произвольной пространственной системы сил.

Произвольную простран­ственную систему сил, как и плос­кую, можно привести к какому - нибудь центру О и заменить од­ной результирующей силой R и парой с моментом М_о. Рассуждая так, что для равновесия этой системы сил необходимо и достаточно, чтобы одновременно было R = 0 и

M_о = 0. Но векторы R и M_о могут обратиться в нуль только тогда, когда равны нулю все их проекции на оси координат, т. е. когда R_x = R_y = R_z = 0 и

M_x = M_y = M_z = 0 или, когда дей­ствующие силы удовлетворяют условиям

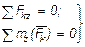
Таким образом, для равновесия произвольной пространственной системы сил необходимо и достаточно, чтобы суммы проекций всех сил на каждую из трех координатных осей и суммы их моментов относительно этих осей были равны нулю.

Принцип решения задач этого раздела остается тем же, что и для плоской системы сил. Установив, равновесие, какого тела будет рассматриваться, заменяют наложенные на тело связи их реакциями и составляют условия равновесия этого тела, рассма­тривая его как свободное. Из полученных уравнений определяются искомые величины.

Для получения более простых систем уравнений рекомендуется оси проводить так, чтобы они пересекали больше неизвестных сил или были к ним перпендикулярны (если это только излишне не усложняет вычисления проекций и моментов других сил).

Новым элементом в составлении уравнений является вычисление моментов сил относительно осей координат.

В случаях, когда из общего чертежа трудно усмотреть, чему равен момент данной силы относительно какой-нибудь оси, рекоменду­ется изобразить на вспомогательном чертеже проекцию рассматри­ваемого тела (вместе с силой) на плоскость, перпендикулярную к этой оси.

В тех случаях, когда при вычислении момента возникают затруд­нения в определении проекции силы на соответствующую плоскость или плеча этой проекции, реко­мендуется разложить силу на две взаимно перпендикулярные состав­ляющие (из которых одна парал­лельна какой-нибудь координат­ной оси), а затем воспользоваться теоремой Вариньона.

ЛЕКЦИЯ 4

Центр тяжести твердого тела.

На любую частицу тела, находящегося вблизи земной поверхности, действует направленная вертикально вниз сила, называемая силой тяжести. Сила тяжести является равнодействующей силы притяжения Земли и центробежной силы, возникающей вследствие вращения тела вместе в Землей.

Для тел, размеры которых очень малы по сравнению с земным радиусом, силы тяжести частиц тела можно считать параллельными друг другу и сохраняющими для каждой частицы постоянную вели­чину при любых поворотах тела. Поле тяжести, в котором выпол­няются эти два условия, называют однородным полем тяжести.

Равнодействующую сил тяжести p₁, p₂, …, p_n, действующих на частицы данного тела, обозначим Р (рис. 36). Модуль этой силы равен весу тела и определяется равенством

.

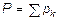Равнодействующая Р сил р_k будет при любых положениях тела про­ходить через одну и ту же неизменно связанную с телом точку С, являющуюся центром параллельных сил тяжести р_k. Эта точка и называется центром тяжести тела. Таким образом, центром тяжести твердого тела называется неизменно связанная с этим телом точка, через которую про­ходит линия действия равнодействующей, сил тяжести частиц данного тела при любом положении тела, в пространстве. Координаты центра тяжести, опре­деляются формулами: Рис. 36.

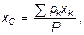
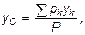
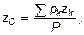
где x_k, у_k, z_k - координаты точек приложения сил тяжестиp_k ча­стиц тела.

Отметим, что согласно определению центр тя­жести — это точка геометрическая; она может лежать и вне преде­лов данного тела (например, для кольца).

Координаты центров тяжести однородных тел.

Для однородного тела вес p_k любой его части пропорционален объему этой части: 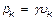, а вес Р всего тела пропорционален объему V этого тела , где γ - вес единицы объема.

Подставив эти значения Р и p_k в предыдущие формулы, мы заметим, что в числителе γ как общий множитель выносится за скобку и со­кращается с γ в знаменателе. В результате получим:

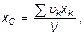
Как видно, центр тяжести однородного тела зависит только от его геометрической формы, а от величины γ не зависит. По этой причине точку С, координаты которой определяются формулами, называют центром тяжести объема V.

Путем аналогичных рассуждений легко найти, что если тело пред­ставляет собой однородную плоскую и тонкую пластину, то для нее

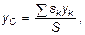
где S - площадь всей пластины, a s_k - площади ее частей.

Точку, координаты которой определяются формулами называют центром тяжести площади S.

Точно так же получаются формулы для координат центра тя­жести линии:

где L — длина всей линии, l — длины ее частей.

Таким образом, центр тяжести однородного тела определяется, как центр тяжести соответствующего объема, площади или линии.

Дата добавления: 2014-12-17