Представление матриц поворота через углы Эйлера

Матричное описание вращения твёрдого тела упрощает многие операции; однако, для того, чтобы полностью описать ориентацию вращающегося твёрдого тела, необходимо использовать все девять элементов матрицы поворота. Непосредственно эти элементы не составляют полной системы обобщённых координат, с помощью которых можно описать ориентацию вращающегося твёрдого тела относительно абсолютной системы координат.

В качестве обобщённых координат можно использовать углы Эйлера j, q и y.

Таблица 3.1. Три системы углов Эйлера

Последова-тельность поворотов	На j вокруг оси OZ	На j вокруг оси OZ	На y вокруг оси OX
На q вокруг оси OU	На q вокруг оси OV	На q вокруг оси OY
На y вокруг оси OW	На y вокруг оси OW	На j вокруг оси OZ

Первая из систем углов Эйлера обычно используется при описании движения гироскопов и соответствует следующей последовательности поворотов (рис. 3.2):

1. Поворот на угол j вокруг оси OZ (R _z, ).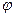

2. Поворот на угол q вокруг повёрнутой оси OU (R _u,q).

3. Поворот на угол y вокруг повёрнутой оси OW (R _w,y).

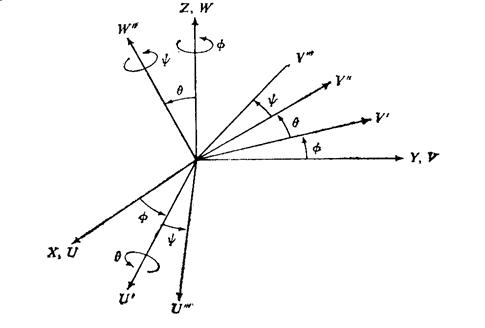
Рисунок 3.2. Первая система углов Эйлера

Результирующая матрица поворота имеет следующий вид:

R _j,q,y = R _z,j × R _u,q × R _w,y = =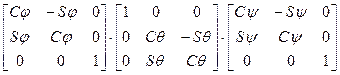

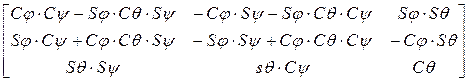= . (3-2)

Поворот, описываемый матрицей R _j,q,y,может быть также получен в результате выполнения последовательности следующих поворотов вокруг осей неподвижной системы координат: сначала на угол y вокруг оси OZ, затем на угол q вокруг оси OX, затем на угол j вокруг оси OZ.

На рисунке 3.3 показана вторая система углов Эйлера, определяемая следующей последовательностью поворотов:

1. Поворот на угол j вокруг оси OZ (R _z,j).

2. Поворот на угол q вокруг оси OV (R _v,q).

3. Поворот на угол y вокруг повёрнутой оси OW (R _w,y).

Результирующая матрица поворота имеет следующий вид:

R _j,q,y = R _z,j × R _v,q × R _w,y = =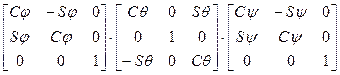

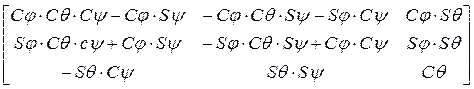= . (3-3)

Поворот, описываемый матрицей R _j,q,yдля этой системы углов Эйлера, может быть получен также в результате выполнения последовательных поворотов: на угол y вокруг оси OZ, на угол q вокруг оси OY, на угол j вокруг оси OZ.

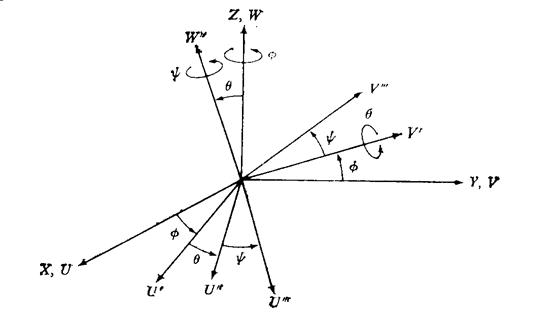
Рисунок 3.3. Вторая система углов Эйлера

Ещё одну систему углов Эйлера составляют так называемые углы крена, тангажа и рыскания. Эти углы обычно применяются в авиации для описания движения самолётов.

Они соответствуют следующей последовательности поворотов:

1. Поворот на угол y вокруг оси OX (R _x,y) – рыскание.

2. Поворот на угол q вокруг оси OY (R _y,q) – тангаж.

3. Поворот на угол j вокруг оси OZ (R _z,j) – крен.

Результирующая матрица поворота имеет вид:

R _j,q,y = R _z,j × R _y,q × R _x,y= =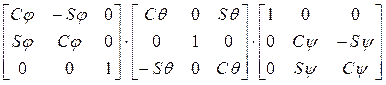

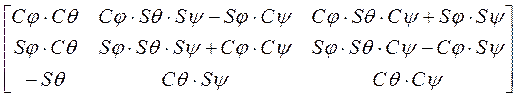= . (3-4)

Поворот, описываемый матрицей R _j,q,yв переменных «крен, тангаж, рыскание» может быть также получен в результате выполнения следующей последовательности поворотов вокруг осей абсолютной и подвижной систем координат: на угол j вокруг оси OZ, затем на угол q вокруг повёрнутой оси OV, на угол y вокруг повёрнутой оси OU (продольная ось аппарата – Z) (рис. 3.4).

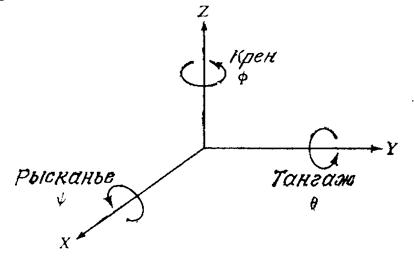
Рисунок 3.4. Крен, тангаж, рысканье (третья система углов Эйлера)

Дата добавления: 2014-12-17