Алгоритм формирования систем координат звеньев

Представление Денавита – Хартенберга

Для описания вращательных и поступательных связей между соседними звеньями Денавит и Хартенберг предложили матричный метод последовательного построения систем координат, связанных с каждым звеном кинематической цепи. Смысл представления Денавита–Хартенберга (ДХ-представление) состоит в формировании однородной матрицы преобразования, имеющей размерность 4×4 и описывающей положение системы координат каждого звена относительно системы координат предыдущего звена. Это дает возможность последовательно преобразовать координаты схвата манипулятора из системы отсчета, связанной с последним звеном, в базовую систему отсчета, являющейся инерциальной системой координат для рассматриваемой динамической системы.

Каждая система координат формируется на основе следующих трех правил:

1) ось z_i-1 направлена вдоль оси i –го сочленения;

2) ось x_i перпендикулярна оси z_i-1 и направлена от нее;

3) ось y_i дополняет оси x_i, z_i до правой декартовой системы координат.

ДХ–представление твердых звеньев зависит от четырех геометрических параметров, соответствующих каждому звену. Эти четыре параметра полностью описывают любое вращательное или поступательное движение и определяются в соответствии с рис. 5.4 следующим образом:

Q_i – присоединенный угол, на который надо повернуть ось x_i-1 вокруг оси z_i-1, чтобы она стала сонаправлена с осью x_i (знак определяется в соответствии с правилом правой руки);

d_i - расстояние между пересечением оси z_i-1 с осью x_i и началом (i -1)-й системы координат, отсчитываемое вдоль оси z_i-1;

a_i - линейное смещение – расстояние между пересечением оси z_i-1 с осью x_i и началом i -й системы координат, отсчитываемое вдоль оси x_i, т. е. кратчайшее расстояние между осями z_i-1 и z_i;

α_i - угловое смещение - угол, на который надо повернуть ось z_i-1 вокруг оси x_i, чтобы она стала сонаправленной с осью z_i (знак определяется в соответствии с правилом правой руки).

Для вращательных сочленений параметры d_i, a_i и α_i являются характеристикамисочленения, постоянными для данного типа робота. В то же время Q_i является переменной величиной, изменяющейся при движении (вращении) i -го звена относительно (i-1)-го.

Для каждого звена манипулятора с n степенями свободы этот алгоритм формирует ортонормированную систему координат. Системы координат нумеруются в порядке возрастания от основания к схвату манипулятора. Взаимное расположение соседних звеньев описывается однородной матрицей преобразования размерностью 4х4.

Параметры систем координат звеньев манипулятора Пума
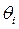
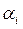
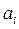
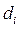
Сочленение i					Пределы измерения
		-90			-160-+160
			431,8 мм	149,09 мм	-225-45
			-20,32 мм		-45-225
		-90		433,07 мм	-110-170
					-100-100
				56,25 мм	-266-266

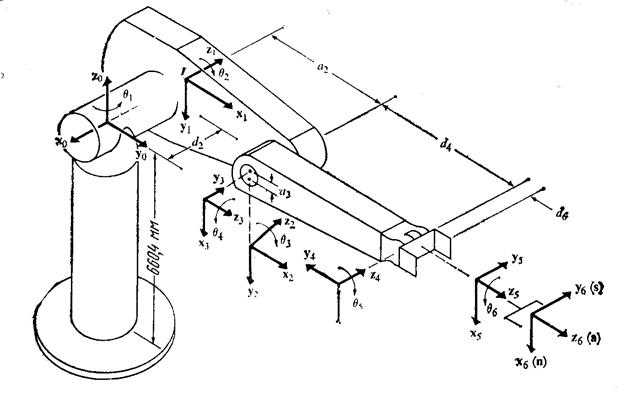
Рисунок 5.4. Формирование систем координат звеньев

Дата добавления: 2014-12-17