Модель геометрических лагов

В этой модели предполагается, что количество лагов бесконечно:

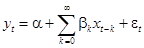, (4)

а коэффициенты 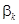убывают в геометрической прогрессии:

, (5)

где – константа, характеризующая скорость убывания коэффициентов регрессии.

Подставив (5) в (4), получим:

(6)

Для оценивания параметров модели (6) используется следующая методика.

Запишем уравнение (6) для периода :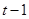

(7)

Несложно показать, что уравнение (6) можно записать в виде:

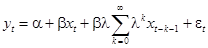(8)

В силу (7), (8):

(9)

где

(10)

Из (9) получим:

(11)

Преобразование уравнения (4) в уравнение (11) называется преобразованием Койка.

Согласно излагаемой методике уравнение (11) используется для оценки параметров модели и построения прогноза.

Следует отметить, что уравнение (11) содержит, во-первых, лагированное значение зависимой переменной и, во-вторых, ошибки 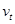, не удовлетворяющие (в силу (10)) условиям классической модели линейной регрессии. Поэтому МНК-оценки коэффициентов регрессии уравнения (11) являются смещенными и несостоятельными.

Для получения состоятельных оценок можно применять метод инструментальных переменных (взяв, например, в качестве инструмента для ) или воспользоваться методом максимального правдоподобия.

Модели авторегрессии

Модель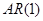

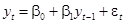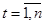, (12)

где 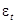независимые нормально распределенные случайные величины с нулевым математическим ожиданием и постоянной дисперсией :

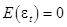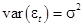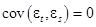, , . (13)

Будем считать, что случайный процесс 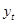является стационарным (в слабом смысле), т.е.

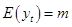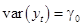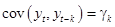
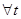, , (14)

(эти величины не зависят от ).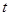

Отметим, что в соответствии с (12), (13):

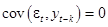при (15)

Из (12) в силу (13) и (14):

Следовательно,

(16)

Отсюда,

(17)

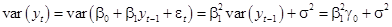
Следовательно,

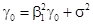(18)

Отсюда:

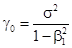(19)

Поскольку дисперсия всегда неотрицательна, из формулы (19) следует, что условие:

(20)

является необходимым условием стационарности процесса .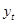

С другой стороны, можно доказать, что при выполнении условия (20) всегда можно построить стационарный процесс 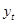, для которого имеет место равенство (12) и выполнены условия (13).

В силу (1)-(4):

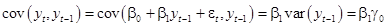
Следовательно,

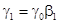(20)

В силу (12)-(15):

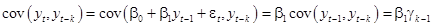
Итак,

(21)

Из (20), (21) следует, что

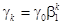(22)

Функция, описывающая зависимость 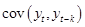от , называется ковариационной функцией (стационарного) случайного процесса .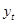

Таким образом, ковариационная функция процесса 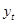определяется формулой (22).

Напомним, что коэффициент корреляции 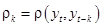находится по формуле:

(23)

Следовательно, в силу равенств (14), (22):

(24)

Функция, описывающая зависимость коэффициента корреляции 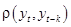от , называется, автокорреляционной функцией (стационарного) случайного процесса .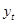

Таким образом, автокорреляционная функция процесса 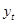определяется формулой (24).

Дата добавления: 2014-12-17