Прогнозирование на несколько периодов вперед

В соответствии с формулой (12):

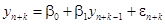(37)

Следовательно,

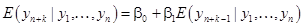(38)

В силу формулы (38) в качестве прогноза 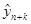можно взять следующее значение:

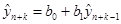. (39)

С помощью формул (36), (39) рекуррентным образом можно построить прогноз на любое количество периодов вперед.

Модель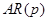

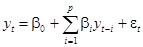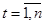, (40)

где 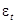независимые нормально распределенные случайные величины с нулевым математическим ожиданием и постоянной дисперсией :

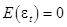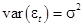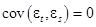, , . (41)

Будем считать, что случайный процесс 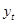является стационарным (в слабом смысле), т.е.

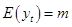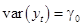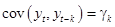
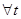, , (42)

(эти величины не зависят от ).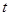

Отметим, что в соответствии с (41), (42):

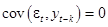при (43)

Из (40) в силу (41) и (42):

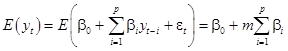
Следовательно,

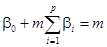(44)

Отсюда,

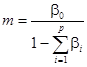(45)

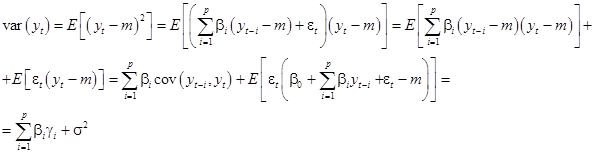(46)

Следовательно,

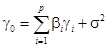(47)

Найдем ковариацию .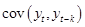

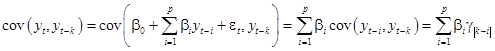
Итак,

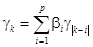(48)

Из (48) следует, что:

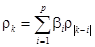(49)

Оценивание параметров модели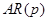

Выборочные коэффициенты корреляции 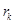вычисляются по формуле (27).

Заменив теоретические коэффициенты корреляции 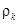на выборочные 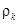получим систему линейных уравнений относительно оценок 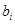коэффициентов :

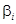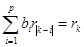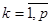, (50)

Уравнения (50) называются уравнениями Юла-Уокера.

Систему (50) можно записать в матричном виде:

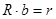(51)

где

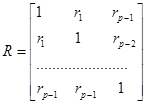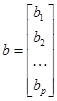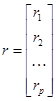, , (52)

Из (51) следует, что:

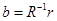(53)

Итак, коэффициенты регрессии 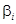, могут быть оценены по формуле (53).

В силу (44):

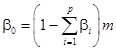(54)

Следовательно, в качестве оценки параметра 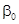можно взять:

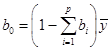(55)

Из (47):

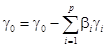(56)

Следовательно, в качестве оценки 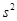параметра можно взять:

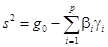(57)

Дата добавления: 2014-12-17