
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Прогнозирование на несколько периодов вперед. Прогнозирование на один период вперед
|
|
|
|
Прогнозирование на один период вперед
В соответствии с формулой (40):
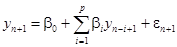 (58)
(58)
Следовательно,
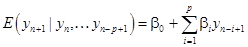 (59)
(59)
В силу формулы (59) в качестве прогноза 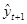 можно взять следующее значение:
можно взять следующее значение:
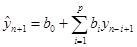 (60)
(60)
В соответствии с формулой (40):
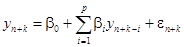 (61)
(61)
Следовательно,
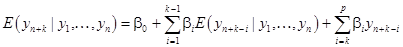 (61’)
(61’)
В силу (61’) прогнозное значение 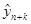 можно искать рекуррентным образом по следующей формуле:
можно искать рекуррентным образом по следующей формуле:
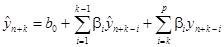 . (62)
. (62)
Определение порядка авторегрессии
Доказано, что при 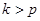 все значения частной автокорреляции
все значения частной автокорреляции 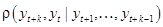 равны нулю.
равны нулю.
Порядок авторегрессии равен значению 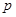 при котором:
при котором:
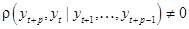 (63)
(63)
и
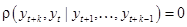
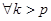 (64)
(64)
С помощью реальных данных можно определить выборочный коэффициент частной автокорреляции.
Выборочный частный коэффициент автокорреляции находится в соответствии с изложенным выше методом (см. тему 5), а именно:
Построим регрессии 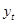 и
и 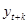 на
на 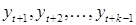 :
:
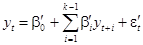 (65)
(65)
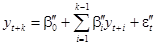 (66)
(66)
где 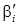 и
и 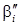 коэффициенты регрессии,
коэффициенты регрессии, 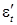 и
и 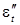 – случайные отклонения.
– случайные отклонения.
Найдем МНК-оценки 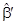 и
и 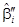 коэффициентов
коэффициентов 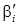 и
и 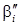
С помощью МНК-оценок 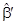 и
и 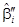 построим прогнозные значения:
построим прогнозные значения:
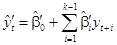 , (67)
, (67)
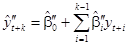 (68)
(68)
С помощью найденных прогнозных значений найдем остатки регрессий:
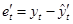 , (69)
, (69)
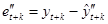 (70)
(70)
Частный коэффициент корреляции между 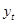 и
и 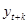 без учета влияния значений
без учета влияния значений 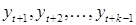 – это коэффициент парной корреляции между остатками
– это коэффициент парной корреляции между остатками 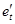 и
и 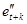 :
:
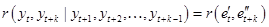 , (71)
, (71)
т.е.
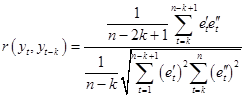 (72)
(72)
Условия стационарности
Характеристическое уравнение:
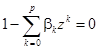 (73)
(73)
Для стационарности процесса 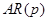 необходимо и достаточно, чтобы все корни уравнения (73) (в том числе комплексные) лежали вне единичного круга, т.е. превосходили по модулю единицу.
необходимо и достаточно, чтобы все корни уравнения (73) (в том числе комплексные) лежали вне единичного круга, т.е. превосходили по модулю единицу.
Для исследования ряда 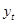 на стационарность используется тест Дики-Фуллера.
на стационарность используется тест Дики-Фуллера.
Рассмотрим модель 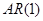
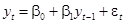 ,
, 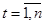 (74)
(74)
В соответствии с материалом Темы 3 t-статистика для коэффициента  для проверки гипотезы
для проверки гипотезы 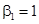 строится по формуле:
строится по формуле:
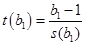 (75)
(75)
где 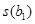 – оценка стандартного отклонения коэффициента
– оценка стандартного отклонения коэффициента 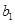 .
.
Если значение t-статистики 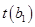 больше (одностороннего) критического значения теста Дики-Фуллера, то гипотеза
больше (одностороннего) критического значения теста Дики-Фуллера, то гипотеза 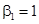 принимается, и ряд
принимается, и ряд 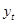 в этом случае считается, что ряд не является стационарным. В противном случае ряд считается стационарным.
в этом случае считается, что ряд не является стационарным. В противном случае ряд считается стационарным.
|
|
|
|
|
Дата добавления: 2014-12-17; Просмотров: 381; Нарушение авторских прав?; Мы поможем в написании вашей работы!