
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Логические модели представления знаний
|
|
|
|
Вопросы, подлежащие изучению
2.1. Формальные логические модели.
2.2. Синтаксис и семантика логики предикатов.
2.3. Правила вывода.
2.4. Системы дедукции.
Пояснения к вопросам
2.1. Традиционно в представлении знаний выделяют формальные логические модели, основанные на классическом исчислении предикатов 1-го порядка, когда предметная область или задача описывается в виде набора аксиом. Все предметы и события, которые составляют основу общего понимания необходимой для решения задачи информации, называются предметной областью.
Объекты предметной области называются сущностями. Между сущностями существуют определенные отношения, которые выражаются с помощью суждений.
Языки, предписанные для описания предметных областей, называются языками представления знаний. Для представления знания в математической логике используют исчисление предикатов.
Описания предметных областей, выполненные в логических языках, называются логическими моделями.
В основе логических моделей лежит формальная система, задаваемая четверкой вида: M = <T, P, A, B>. Множество T есть множество базовых элементов различной природы, например слов из некоторого ограниченного словаря, деталей детского конструктора, входящих в состав некоторого набора и т.п. Важно, что для множества T существует некоторый способ определения принадлежности или непринадлежности произвольного элемента к этому множеству. Процедура такой проверки может быть любой, но за конечное число шагов она должна давать положительный или отрицательный ответ на вопрос, является ли x элементом множества T. Обозначим эту процедуру П(T).
Множество P есть множество синтаксических правил. С их помощью из элементов T образуют синтаксически правильные совокупности. Например, из слов ограниченного словаря строятся синтаксически правильные фразы, из деталей детского конструктора с помощью гаек и болтов собираются новые конструкции. Декларируется существование процедуры П(P), с помощью которой за конечное число шагов можно получить ответ на вопрос, является ли совокупность X синтаксически правильной.
В множестве синтаксически правильных совокупностей выделяется некоторое подмножество A. Элементы A называются аксиомами. Как и для других составляющих формальной системы, должна существовать процедура П(A), с помощью которой для любой синтаксически правильной совокупности можно получить ответ на вопрос о принадлежности ее к множеству A.
Множество B есть множество правил вывода. Применяя их к элементам A, можно получать новые синтаксически правильные совокупности, к которым снова можно применять правила из B. Так формируется множество выводимых в данной формальной системе совокупностей. Если имеется процедура П(B), с помощью которой можно определить для любой синтаксически правильной совокупности, является ли она выводимой, то соответствующая формальная система называется разрешимой. Это показывает, что именно правило вывода является наиболее сложной составляющей формальной системы.
Для знаний, входящих в базу знаний, можно считать, что множество A образуют все информационные единицы, которые введены в базу знаний извне, а с помощью правил вывода из них выводятся новые производные знания. Другими словами формальная система представляет собой генератор порождения новых знаний, образующих множество выводимых в данной системе знаний. Это свойство логических моделей делает их притягательными для использования в базах знаний. Оно позволяет хранить в базе лишь те знания, которые образуют множество A, а все остальные знания получать из них по правилам вывода.
2.2. Математическая логика лежит в основе различных представлений в ИИ. Объектами изучения естественных и формальных языков являются, в частности, синтаксис (который позволяет распознавать фразы среди наборов слов) и семантика (которая придает определенное значение фразам).
Язык логики предикатов задается синтаксисом. Логика предикатов допускает четыре типа выражений: константы, переменные, предикатные имена и функциональные имена.
Определение семантических знаний компонент и формул логики предикатов базируется на интерпретации логической формулы. Прежде всего задаются уникальное семантическое значение для каждого базисного выражения. Затем вводится семантические правила вычисления семантических значений сложных логических формул по известным семантическим значениям компонент.
2.3. Исчисление предикатов содержит правила вывода, применимые к одним логическим формулам для получения других. Особенно важны правила «modus ponens» (правило отделения):
если 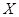 и
и  - теоремы, то
- теоремы, то 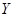 есть теорема
есть теорема
и «обобщения»:
если  не связана в теореме
не связана в теореме 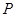 , то
, то  - теорема.
- теорема.
Правила вывода порождают некое множество формул из исходных формул. В исчислении предикатов выведенные формулы называются «теоремами», а последовательность примененных для их получения правил вывода – «доказательством теоремы».
При доказательстве теорем обычно используют процедуры опровержения. Множество гипотез 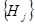 , подходящих для доказательства теоремы, добавляют к множеству присущих области знаний аксиом
, подходящих для доказательства теоремы, добавляют к множеству присущих области знаний аксиом  и стремятся получить опровержение (или прийти к противоречию), присоединяя
и стремятся получить опровержение (или прийти к противоречию), присоединяя  - отрицание утверждения теоремы – к системе
- отрицание утверждения теоремы – к системе 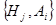 и пытаясь доказать формулу
и пытаясь доказать формулу  .
.
В большинстве систем относящиеся к области представления знаний знания делятся на факты и правила.
Факты – данные (представленные предикатами), касающиеся области знаний. Например, данные о персонале университета составляют множество фактов.
Правила – данные, представленные с помощью импликации (или в иной эквивалентной логической форме). Например, правило: Если
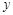 -профессор факультета
-профессор факультета  и
и  -студент факультета
-студент факультета 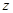 при
при  , то
, то 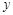 может служит внешним экзаменатором для
может служит внешним экзаменатором для  .
.
Задача доказательства теоремы состоит в установлении выводимости из фактов и правил некой формулы (целы), представляющий интерес.
2.4. Для доказательства теорем можно использовать системы дедукции.
В системах прямой дедукции новые знания получают, применяя выводы к фактам и правилам. Алгоритм завершает работу при получении некоторого знания, эквивалентного цели. Систему прямой дедукции можно толковать как систему, в которой применяется теорема о прямой дедукции:
Если 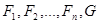 - логические выражения, то
- логические выражения, то 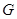 является логическим следствием из
является логическим следствием из  тогда и только тогда, когда логическое выражение
тогда и только тогда, когда логическое выражение  тождественно ложно, т.е. не выполнимо.
тождественно ложно, т.е. не выполнимо.
В системах обратной дедукции выводы применяют к цели и к правилам, чтобы построит новые частичные цели. Алгоритм завершает работу при получении некоторого знания, эквивалентного цели. Систему обратной дедукции можно толковать как систему, в которой применяется теорема об обратной дедукции:
Если 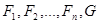 - логические выражения, то
- логические выражения, то 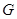 является логическим следствием из
является логическим следствием из  тогда и только тогда, когда логическое выражение
тогда и только тогда, когда логическое выражение 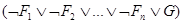 тождественно истинно, т.е. общезначимо.
тождественно истинно, т.е. общезначимо.
В системах обратной дедукции правила и цели преобразуют в конъюнкты, чтобы применить правило согласия:
Пусть 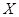 - высказывание, а
- высказывание, а  и
и  - дизъюнкты, тогда
- дизъюнкты, тогда  .
.
Правило согласия двойственно правилу резолюций:
Пусть 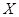 - высказывание, а
- высказывание, а  и
и  - дизъюнкты, тогда
- дизъюнкты, тогда  .
.
Применение правила резолюций к дизъюнктам  и
и  называется резолюцией этих дизъюнктов, адизъюнкт
называется резолюцией этих дизъюнктов, адизъюнкт  - их резольвентой.
- их резольвентой.
Пример 1. Пусть задано множество дизъюнктов  .
.
Для удобства пронумеруем дизъюнкты:
1.  2.
2. 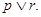 3.
3.  4.
4. 
Тогда 5.  6.
6. 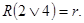 7.
7. 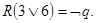 8.
8. 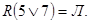
Пример 2. Рассмотрим системы прямой и обратной дедукции.
- Факт(1).
По-русски: Иванов – профессор факультета информационных технологий.
Логически: Проф(Инфо, Иванов_1).
- Факт(2).
По-русски: Мария – студентка факультета радиотехники.
Логически: Студ(Рад, Мария_2).
- Правило(1).
По-русски: Если 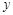 -профессор факультета
-профессор факультета  и
и  -студент факультета
-студент факультета 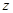 при
при  , то
, то 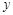 может служит внешним экзаменатором для
может служит внешним экзаменатором для  .
.
Логически: Проф(x,y)  Студ(z,w)
Студ(z,w)  Равно(x,z)
Равно(x,z)  Экзам(y,w).
Экзам(y,w).
- Предложение – цель(1).
По-русски: Может ли Иванов служит внешним экзаменатором для Марии?
Логически: Экзам(Иванов_1, Мария_2).
1. Системы прямой дедукции.
Докажем теорему: (Факт(1)  Факт(2)
Факт(2)  Правило(1))
Правило(1))  Цель(1).
Цель(1).
Преобразуем Факт(1) и Правило (1) в дизъюнкты, чтобы применить правило резолюции.
Этап(1).
R(Факт(1), Правило(1))=R(Проф(Инфо, Иванов_1), 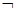 Проф(x,y)
Проф(x,y) 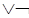 Студ(z,w)
Студ(z,w) 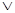 Равно(x,z)
Равно(x,z) 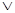 Экзам(y,w))= Правило(2): (
Экзам(y,w))= Правило(2): (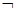 Студ(z,w)
Студ(z,w) 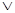 Равно(Инфо,z)
Равно(Инфо,z) 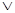 Экзам(Иванов_1,w)).
Экзам(Иванов_1,w)).
При резолюции проведена унификация: x принимает значение Инфо, а y – значение Иванов_1.
Этап(2).
R(Факт(1), Правило(2))=R(Студ(Рад, Мария_2), 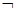 Студ(z,w)
Студ(z,w) 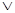 Равно(Инфо,z)
Равно(Инфо,z) 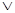 Экзам(Иванов_1,w))= Факт(3): (Равно(Инфо, Рад)
Экзам(Иванов_1,w))= Факт(3): (Равно(Инфо, Рад) 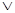 Экзам(Иванов_1, Мария_2)= Факт(3): (Экзам(Иванов_1, Мария_2), т.к. Равно(Инфо, Рад)=Л.
Экзам(Иванов_1, Мария_2)= Факт(3): (Экзам(Иванов_1, Мария_2), т.к. Равно(Инфо, Рад)=Л.
При резолюции проведена унификация: z принимает значение Рад, а w – значение Мария_2.
Унификация (приведение к единообразию):
- сопоставление констант, т.е. константа унифицируется с константой;
- переменная унифицируется с константой и принимает значение константы;
- переменная унифицируется с переменной и они становятся одной и той же переменной.
Этап(3).
Факт(3) соответствует Цели(1). Следовательно она подтверждена, т.е. Иванов может служит внешним экзаменатором для Марии.
2. Системы обратной дедукции.
Докажем теорему: (Факт(1)  Факт(2)
Факт(2)  Правило(1))
Правило(1))  Цель(1).
Цель(1).
В системах обратной дедукции правила и цели преобразуют в конъюнкты, чтобы применить правило согласия S (S – двойственна к R)
Этап(1).
S(Цель(1), 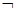 Правило(1)) = S(Экзам(Иванов_1, Мария_2), Проф(x,y)
Правило(1)) = S(Экзам(Иванов_1, Мария_2), Проф(x,y)  Студ(z,w)
Студ(z,w)  Равно(x,z)
Равно(x,z)  Экзам(y,w)) = Цель(2): (Проф(x, Иванов_1)
Экзам(y,w)) = Цель(2): (Проф(x, Иванов_1)  Студ(z, Мария_2)
Студ(z, Мария_2)  Равно(x,z)).
Равно(x,z)).
Здесь проведена унификация: y принимает значение Иванов_1, а w – значение Мария_2.
Этап(2).
S(Цель(2), 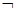 Факт(1)) = S(Проф(x, Иванов_1)
Факт(1)) = S(Проф(x, Иванов_1)  Студ(z, Мария_2)
Студ(z, Мария_2)  Равно(x,z),
Равно(x,z), 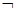 Проф(Инфо, Иванов_1)) = Цель(3): (Студ(z, Мария_2)
Проф(Инфо, Иванов_1)) = Цель(3): (Студ(z, Мария_2)  Равно(Инфо, z)).
Равно(Инфо, z)).
Здесь проведена унификация: x принимает значение Инфо.
Этап(3).
S(Цель(3), 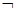 Факт(2)) = S(Студ(z, Мария_2)
Факт(2)) = S(Студ(z, Мария_2)  Равно(Инфо, z),
Равно(Инфо, z), 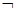 Студ(Рад, Мария_2))=
Студ(Рад, Мария_2))= 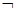 Равно(Инфо, Рад) = И.
Равно(Инфо, Рад) = И.
Следовательно Цел(1) подтверждена, т.е. Иванов может служит внешним экзаменатором для Марии.
3. СЕТЕВЫЕ МЕТОДЫ ПРЕДСТАВЛЕНИЯ ЗНАНИЙ 
Вопросы, подлежащие изучению
3.1. Семантические сети.
3.2. Поиск решения в семантической сети.
Пояснения к вопросам
3.1. Недостаток логического формализма – его неструктурированность. Графические представления позволяют визуализировать модель мира. Термин семантическая означает «смысловая», а сама семантика — это наука, устанавливающая отношения между символами и объектами, которые они обозначают, то есть наука, определяющая смысл знаков.
Семантическая сеть — это ориентированный граф, вершины которого — понятия, а дуги — отношения между ними.
В качестве понятий обычно выступают абстрактные или конкретные объекты, а отношения — это связи типа: «это» («АКО — A-Kind-Of», «is»), «имеет частью» («has part»), «принадлежит», «любит». Характерной особенностью семантических сетей является обязательное наличие трех типов отношений:
- класс — элемент класса (цветок — роза);
- свойство — значение (цвет — желтый);
- пример элемента класса (роза — чайная).
Можно предложить несколько классификаций семантических сетей, связанных с типами отношений между понятиями.
По количеству типов отношений:
- однородные (с единственным типом отношений).
- неоднородные (с различными типами отношений).
По типам отношений:
- бинарные (в которых отношения связывают два объекта).
- N-арные (в которых есть специальные отношения, связывающие более двух понятий).
Наиболее часто в семантических сетях используются следующие отношения:
- связи типа «часть — целое» («класс — подкласс», «элемент —множество», и т. п.);
- функциональные связи (определяемые обычно глаголами «производит», «влияет»...);
- количественные (больше, меньше, равно...);
- пространственные (далеко от, близко от, за, под, над...);
- временные (раньше, позже, в течение...);
- атрибутивные связи (иметь свойство, иметь значение);
- логические связи (И, ИЛИ, НЕ);
- лингвистические связи и др.
3.2. Проблема поиска решения в базе знаний типа семантической сети сводится к задаче поиска фрагмента сети, соответствующего некоторой подсети, отражающей поставленный запрос к базе.
Пример 3. На рис. 1 изображена семантическая сеть. В качестве вершин выступают понятия «человек», «т. Иванов», «Волга», «автомобиль», «вид транспорта» и «двигатель».

Рис. 1. Семантическая сеть
Если имеется цель -запрос Любит(Иванов, x), то поиск решения (доказательства) сводится к поиску конкретизации для x. В данном случае x – автомобиль.
Данная модель представления знаний была предложена американским психологом Куиллианом. Основным ее преимуществом является то, что она более других соответствует современным представлениям об организации долговременной памяти человека.
Недостатком этой модели является сложность организации процедуры поиска вывода на семантической сети.
|
|
|
|
|
Дата добавления: 2014-12-17; Просмотров: 972; Нарушение авторских прав?; Мы поможем в написании вашей работы!