Энергетическая диаграмма квантовой ямы с конечными стенками и дополнительным провалом

План лекции

ОСОБЕННОСТИ ЭНЕРГЕТИЧЕСКОГО СПЕКТРА ЧАСТИЦ В СИСТЕМАХ ПОНИЖЕНОЙ РАЗМЕРНОСТИ

ЛЕКЦИЯ №6

1.1. Энергетическая диаграмма квантовой ямы с конечными стенками и дополнительным провалом.

1.2. Структура со сдвоенной квантовой ямой.

Энергетический спектр частицы в системе с δ-образным барьером.

В реальности мы имеем дело с потенциальными ямами, стенки которых имеют конечную высоту (см. рис. 1.9, а). Рассмотрим влияние конечной высоты стенок на разрешенные значения энер­гии основного и первого возбужденного состояний КЯ при нали­чии провала.

В этом случае необходимо дополнительно учесть возможность проникновения частицы под барьеры (т.е. в областях 4 и 5, см. рис. 1.9, а).Решение уравнения (1.8.1) для этих областей 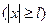можно записать в виде

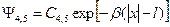(1.8.11)

где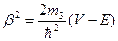

Учитывая граничные условия при x = ±d и x = ±l, можно было бы записать систему алгебраических уравнений, определяющую разрешенные значения K и E. Однако при этом пришлось бы ис­кать совместное решение системы из восьми уравнений. Для уп­рощения расчетов лучше учесть симметрию задачи и вместо гра­ничных условий для x < 0 использовать граничные условия при x = 0. При этом получим:

для четных состояний

(1.8.12)

для нечетных

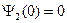(1.8.13)

Учитывая (1.7.12), (1.7.13) и граничные условия при x=d

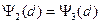
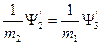(1.8.14)

и при x = l

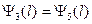
(1.8.15)

получим две системы по пять уравнений, решения которых и опреде­лят разрешенные значения K и E длячетных и нечетных состоянии.

Соответствующие дисперсионные уравнения для определения разрешенных значений энергии и в этом случае (V≠∞) удается представить в виде (1.8.6) и (1.8.9), но уравнение для основного четного состояния теперь будет иметь вид

(1.8.16)

Рис. 1. 12. Графическое решение дисперсионных уравнений (1.8.6) и (1.8.9) с учетом (1.8.16) и (1.8.17): 1-K₁l; 2,4,6-F₀(K₁l); 3,5, 7-F₁ (K₁l); 2,3-m₂=m₁, U=0, V=∞; 4,5- m₂=m₁, U=0, V≠∞; 6,7 - m₂<m₁, U≠0, V≠∞

а уравнение для первого возбужденного (нечетного) состояния может быть записано как

(1.8.17)

Решение дисперсионных уравнений (1.8.6) и (1.8.9) с учетом (1.8.16) и (1.8.17) представлено на рис. 1.12.

Анализ показывает, что понижение высоты стенок КЯ уменьшает значения разрешенных уровней энергии как для ос­новного четного, так и для возбужденного состояния. Такому понижению способствует и увеличение т₃ (эффективной массы материала барьеров). В результате условие существования основ­ного четного уровня в широкой части потенциальной ямы прини­мает вид

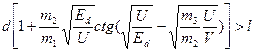(1.8.18)

Оценки [10] показывают, что, например, для структуры, у кото­рой барьеры изготовлены из А1Аs, широкая часть КЯ - из твердого раствора In_0.53Gа_0.47 Аs, провал - из InAs с параметрами V= 1,32 эВ, U=0,24эВ, d = 9,2 A, l=18,2 А, m₁= 0,046 m₀, т₂ = 0,023 m₀, m₃= 0,124m₀, уровни энергии основного и первого возбужденного состояний равны соответственно 0,09 и 1,22 эВ. В то же время для аналогичной структуры без провала эти же уровни соответствуют значениям 0,22 и 0,94 эВ. Таким образом, наличие провала может изменять положение уровней на несколько десятых электрон-вольт.

1.2. Структура со сдвоенной квантовой ямой. Энергетический спектр частицы в системе с δ-образным барьером.

Выше мы рассмотрели поведение частиц в системах, содержа­щих изолированные КЯ и потенциальные барьеры. Как уже отме­чалось, накопленный к настоящему времени опыт и достижения техники для выращивания эпитаксиальных структур позволяют создавать и более сложные гетерокомпозиции, содержащие полу­проводниковые слои со сложным потенциальным профилем. С этой точки зрения большой интерес представляет изучение энерге­тического спектра частиц в связанных квантовых ямах, так как в таких системах возможно направленное регулирование энергети­ческого спектра и скоростей рассеяния электронов с помощью из­менения не только формы КЯ, но и связи между квантовыми яма­ми. Структуры со связанными КЯ стали основой многих электрон­ных и оптоэлектронных приборов. На их основе созданы лазеры инфракрасного (ИК) диапазона, приемники ИК-излучения, элемен­ты нелинейной оптики и быстродействующие транзисторы.

Для выяснения влияния, оказываемого сближением изолиро­ванных квантовых ям, рассмотрим систему, состоящую из двух одинаковых одномерных прямоугольных квантовых ям, разделен­ных проницаемым потенциальным барьером (рис. 1.13).

Обсудим прежде всего качественные изменения. Известно, что энергетический спектр такой системы имеет вид дублетов. Волновая функция в данном случае является реше­нием уравнения (1.1.2) с потенциалом, показанным на рис. 1.13. Если квантовые ямы достаточно удалены друг от друга, то между ними волновая функция практически равна нулю. Решение (1.1.2) в окрестности каждой КЯ в этом случае будет практически совпадать с решением (1.4.12) для изолированной квантовой ямы с тем отличием, что величина 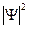вследствие нормировки умень­шится вдвое. Волновая функция для наинизшего квантового состояния приведена на рис. 1.13, а.

Однако для данной задачи возможно и другое решение урав­нения Шредингера (рис. 1.13, б). Единственное различие между -функциями, показанными рис. 1.13, состоит в изменении знака

Рис. 1.13. Потенциальный профиль и вол­новые функции для системы из двух пря­моугольных квантовых ям

в одной из КЯ и означает, что волновая функция (включая зави­симость от времени) в одной из ям отличается по фазе на 180° от в другой яме. Принято говорить, что волновая функция, пред­ставленная на рис. 1.1.3, а, симметрична, а волновая функция (рис. 1.13,б)- антисимметрична.

Между значениями энергии для обоих решений разницы прак­тически нет, что следует из одинаковой для формы 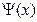, а следо­вательно, одинаковой средней кинетической 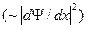энергии и средней потенциальной энергии.

При сближении квантовых ям волновые функции изменяют форму (рис. 1.14). В этом случае волновая функция, показанная на рис. 1.14, а, будет давать меньшее значение полной энергии E, по­скольку для нее среднее значение потенциальной энергии приблизи­тельно такое же, как и в случае, приведенном на рис. 1.14, б, тогда как среднее значение кинетической энергии меньше, так как меньше среднее значение .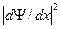

Рис. 1.14. Изменение волновых функций при изменении рас­стояния между квантовыми ямами

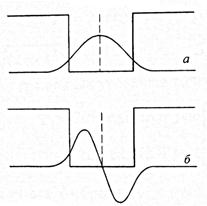
В предельном случае (рис. 1.15), когда ширина барьера между ямами равна нулю, т. е. ямы только что соприкоснулись, -функция (рис. 1.15, а) есть не что иное, как волновая функция основного состояния для квантовой ямы шириной 2W. Поскольку, согласно (1.4.2) и (1.4.7), энергия глубо­ких состояний E ~ En² /w² (w²- ширина рассматриваемой ямы), со­ответствующее значение Е составит примерно 1/4 энергии Е для квантовых ям, показанных на рис. 1.13. Аналогично волновая функ­ция, приведенная на рис. 1.15, б, есть волновая функция с п=2 для КЯ шириной 2W. Таким образом, значение Е, связанное с этой функцией , будет примерно такое же, что и Е для волновой функции на рис. 1.13, так как n увеличилось в два раза (равенство будет точным для КЯ с бесконечно высокими стенками).

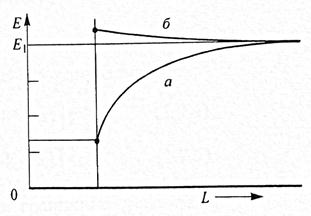
Зависимость энергии для этих двух состояний от расстояния L между КЯ показана на рис. 1.16. Для обоих состояний исходным является значение энергии Е₁ при L =∞ (Е₁, - энергия частицы в состоянии n = 1 для прямоугольной КЯ конечной глубины). Из рис. 1.16 следует также, что при любом значении L уровень Е₁, соответствующий изолированной квантовой яме, расщепляет­ся на два уровня (образуется дублет), причем это расщепление растет с уменьшением расстояния между КЯ. При этом, если частица находится в состоянии с более низкой энергией, то волно­вые функции в обеих КЯ оказываются в одной фазе; если частица находится во втором состоянии, то волновые функции оказываются в противоположных фазах.

Отметим, что расщепление уровней во взаимодействующих квантовых ямах анало­гично расщеплению резонансных час­тот в связанных резонансных контурах.

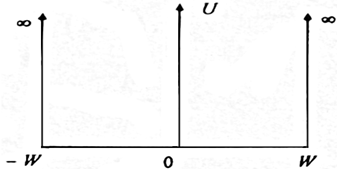
Рассмотрим более подробно энерге­тический спектр частицы в системе, со­стоящей из двух квантовых ям, разделенных 8-образным барьером (рис. 1.17). Распределение потенциала можно записать в виде

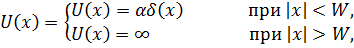
причем α > 0.

Рис. 1.15. Волновые функ­ции для предельного слу­чая, когда барьер только что исчез	Рис. 1.16. Зависимости энергии от L для симметричного (а) и антисиммет­ричного (б) состояний в связанных квантовых ямах

Для 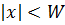состояния частицы в этом потенциале описываются уравнением Шредингера

(1.9.1)

Рис. 1.17. Энергетическая диаграмма КЯ с δ-образным потенциалом

В интервале 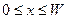решение (1.9.1) имеет вид

(1.9.2)

а для

(1.9.3)

здесь

С учетом граничных условий в точках 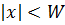получаем

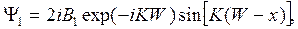(1.9.4)

(1.9.5)

При наличии δ-образного потенциала граничные условия в точке x = 0 принимают вид

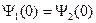
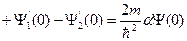
Отсюда получаем выражение, определяющее спектр четных раз­решенных состояний в данной системе,

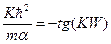(1.9.6)

Анализируя (1.9.6) в пределе и 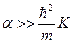(последнее неравенство ограничивает рассмотрение состояний с достаточно низкой энергией), для четных (симметричных) состояний получим

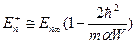(1.9.7)

здесь 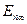- энергия п -го уровня в БПЯ шириной W, найденная по формуле (1.4.7), п = 1, 2, 3,...

Для нечетных состояний волновая функция при x = 0 должна равняться нулю. Согласно (1.9.4) и (1.9.5) данное условие выпол­няется, если .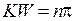

При этом энергия частицы, находящейся в нечетном (антисим­метричном) состоянии, будет определяться выражением

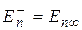(1.9.8)

т. е. в нечетном состоянии частица как бы «не чувствует» наличия δ-образного потенциала в точке x = 0 симметричной системы.

Сопоставляя (1.9.7) и (1.9.8), заметим, что 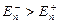. Именно та­кое расположение состояний и вытекало из предшествующего рас­смотрения подобной системы.

Дата добавления: 2014-11-28