Тема: Матриці. Дії з матрицями

ПРАКТИЧНЕ ЗАНЯТТЯ № 1

ВСТУП

В основу даного посібника покладено практичні вимоги до курсу «Алгебра та геометрія», що відповідають навчальному плану ОКР «бакалавр» напряму підготовки «Інформатика».

Запропоноване видання призначене для проведення практичних робіт, самостійного опрацювання студентами окремих розділів лінійної алгебри та виконання індивідуальних завдань із названої дисципліни.

Дисципліна «Алгебра та геометрія» відноситься до загально професійних дисциплін фундаментальної науково-математичної підготовки. Вона забезпечує рівень знань і вмінь відповідно до державного стандарту, відповідає фундаменталізації освіти, сприяє формуванню світогляду і розвитку логічного мислення студентів. Дисципліна «Алгебра та геометрія» є однією з найважливіших розділів математики. Її матеріал є основою для вивчення цілого ряду дисциплін: математичного аналізу, алгебри, фізики, методів обчислень, математичного моделювання. Зокрема матеріал розглянутих тем найбільш тісно пов’язаний з аналітичною геометрією, диференціальною геометрією, тензорним численням, функціональним аналізом.

У зв’язку зі сказаним вище, метою даного посібника є забезпечення високого рівня теоретичних і практичних знань з початкових розділів курсу лінійної алгебри: «Матриці», «Визначники», «Розв’язання систем лінійних алгебраїчних рівнянь».

Основне завдання видання –навчити студентів вільно користуватися поняттями та методами лінійної алгебри (дослідження систем лінійних алгебраїчних рівнянь, обчислення визначників тощо).

У результаті вивчення матеріалу основ лінійної алгебри студент повинен:

ЗНАТИ:

– основні поняття, факти та теореми лінійної алгебри;

– теоретичні основи і суть методів лінійної алгебри;

ВМІТИ:

– застосовувати основні поняття, твердження та теореми до розв’язання задач;

– наводити приклади, які демонструють суть методів лінійної алгебри.

Матрицею розміру (розмірності) 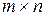, де 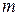– число рядків, – число стовпців, називається прямокутна таблиця з 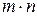елементів деякої множини. Якщо елементами матриці є числа, то матриця називається числовою, якщо вектори, то – векторною, якщо функції, то – функціональною. Розглянемо числову матрицю. Місце кожного елемента 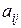матриці однозначно визначається номером рядка 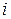й стовпця 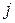, на перетині яких він знаходиться. Позначають:

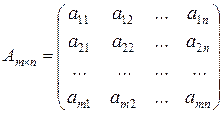або ,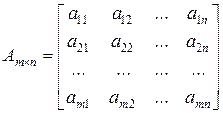

або .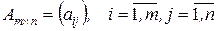

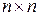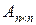Матриця, у якої число рядків дорівнює числу стовпців, називається квадратною (квадратну матрицю розмірності називають матрицею -го порядку і позначають або ).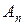

Елементи 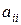, , 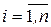у яких номери рядка й стовпця, на перетині яких вони знаходяться, співпадають, утворюють головну діагональ.

Квадратна матриця, у якої всі елементи, окрім головної діагоналі, дорівнюють нулю, називається діагональною.

Діагональна матриця, у якої всі елементи головної діагоналі дорівнюють одиниці, називається одиничною. Позначають:

.

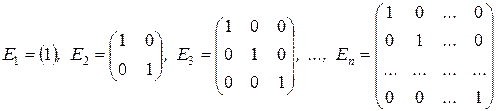Квадратна матриця називається верхньотрикутною (нижньотрикутною), якщо всі елементи, розташовані нижче (вище) головної діагоналі, дорівнюють нулю.

Приклад. Верхньотрикутна 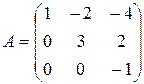та нижньотрикутна 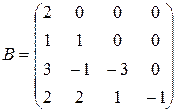матриці.

Квадратна матриця, всі елементи якої дорівнюють нулю, називається нульовою і позначається:

.

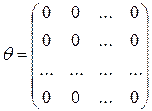Матриці і називаються рівними, якщо вони мають однакові розміри й рівні відповідні елементи, тобто

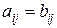, якщо , де , .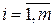

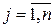Якщо для всіх елементів матриці виконується умова 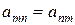(симетрія відносно головної діагоналі), то матриця називається симетричною.

Приклад.

.

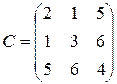Матриця, що містить один рядок, називається вектором або матрицею-рядком, а матриця, що містить один стовпець, також називається вектором або матрицею-стовпцем. Їх вид:

– матриця-стовпець, 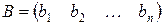– матриця-рядок.

Матриця розміру 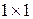, що складається з одного числа, ототожнюється з цим числом, тобто 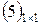є число 5.

Дата добавления: 2014-12-17