Приклади розв’язування задач. Матричний спосіб розв’язання СЛАР

Матричний спосіб розв’язання СЛАР

Систему лінійних алгебраїчних рівнянь із n невідомими (*) можна записати в матричному виді: 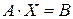, де A – матриця системи, X – матриця-стовпець невідомих 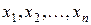, а B – матриця-стовпець вільних членів. Якщо A – невироджена матриця, то після множення ліворуч на 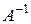обидві частини матричного рівняння 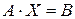, одержимо 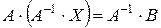. Taк як 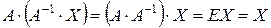, то очевидно

.

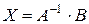1. Розв’яжіть систему лінійних алгебраїчних рівнянь: а) за теоремою Крамера; б) матричним способом:

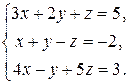
Розв’язання:

а) Обчислимо визначник системи 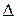й визначники 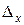, , 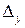, 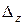що отримані з визначника заміною першого, другого, третього стовпців стовпцем вільних членів:

, ,

, .

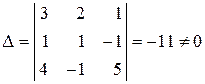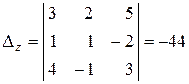За формулами Крамера одержуємо єдиний розв’язок системи:

, , .

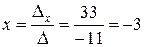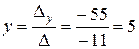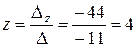Відповідь: .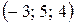

б) Перепишемо вихідну систему у вигляді

,

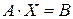де , , .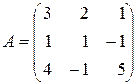

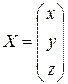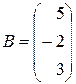Оскільки 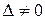, то матриця 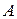має обернену. Знайдемо її методом алгебраїчних доповнень:

, , ,

, , ,

, , ,

.

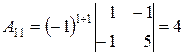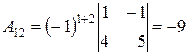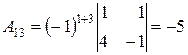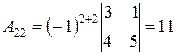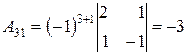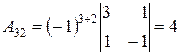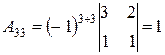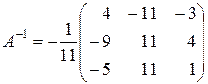Знайдемо розв’язок:

.

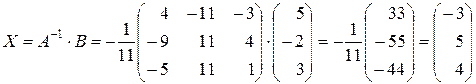Відповідь: .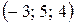

2. Розв’яжіть СЛАР: а) за правилом Крамера; б) шляхом зведення її до матричного рівняння. Порівняйте отримані результати.

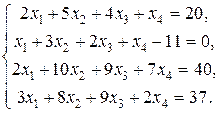
Розв’язання:

а) Знайдемо визначник матриці системи:

.

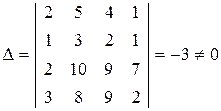За теоремою Крамера дана СЛАР має єдиний розв’язок. Знайдемо значення визначників 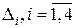матриць, отриманих з вихідної заміною 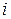-ого стовпця стовпцем вільних членів. Отримаємо:

, ,

, .

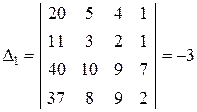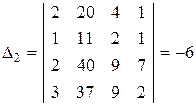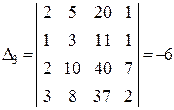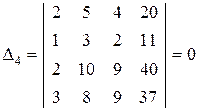Значення змінних знайдемо зі співвідношень:

, , , .

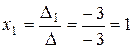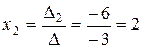б) Запишемо вихідну систему у матричному вигляді:

.

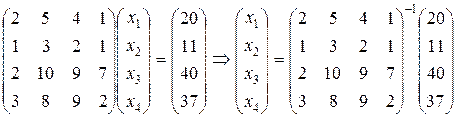На стор. 26-28 знайдено обернену матрицю:

.

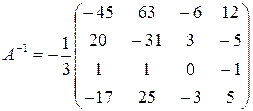Тоді:

.

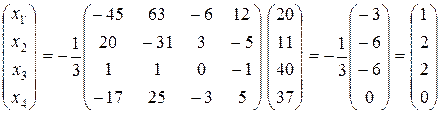Отже, 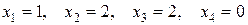. Як бачимо, розв’язки СЛАР, що знайдені різними методами, співпадають між собою.

Підстановкою отриманих значень у вихідну систему легко переконатись, що набір дійсно є її розв’язком.

Дата добавления: 2014-12-17