
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Практичне заняття № 7
|
|
|
|
Тема: Систематизація та узагальнення знань з розділів лінійної алгебри: «Матриці», «Визначники», «Системи лінійних алгебраїчних рівнянь»
Дайте відповіді на наступні питання.
1. Чи можна додати матриці розмірами  і
і  ?
?
2. Чи можна помножити матрицю розмірами  на матрицю з такими ж розмірами?
на матрицю з такими ж розмірами?
3. Які розміри має матриця 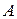 , якщо відомо, що
, якщо відомо, що 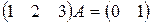 ?
?
4. Наведіть приклади рядка 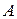 та стовпця
та стовпця 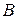 , для яких існує добуток: а)
, для яких існує добуток: а) 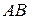 ; б)
; б) 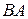 ; в)
; в) 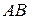 и
и 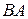 ; г)
; г) 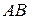 ,
, 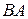 та
та 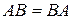 .
.
5. Яка матриця відіграє роль одиниці в операції множення матриць з розмірами 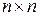 ?
?
6. Для яких матриць  існує
існує 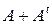 ?
?
7. Відомо, що  . Визначте значення
. Визначте значення 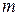 та
та  .
.
8. Знайдіть добутки матриць: а) 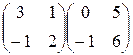 ; б)
; б) 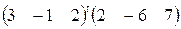 .
.
9. Знайдіть 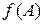 , якщо
, якщо  .
.
10. Розв’яжіть матричне рівняння  , якщо
, якщо
 .
.
11. Дано матриці  . Чи існують добутки
. Чи існують добутки 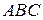 ,
,  ,
,  ?
?
12. Чи існує визначник матриці  ?
?
13. Як зміниться визначник  -го порядку, якщо всі його стовпці записати в зворотному порядку?
-го порядку, якщо всі його стовпці записати в зворотному порядку?
14. Використовуючи властивість лінійності визначника (№ 7), обчисліть
 .
.
15. Як пов’язані між собою доповняльний мінор та алгебраїчне доповнення елемента 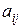 визначника матриці
визначника матриці  -го порядку?
-го порядку?
16. Як зміниться визначник порядку  , якщо перший стовпець переставити на останнє місце, а інші стовпці пересунути вліво, зберігаючи їх порядок?
, якщо перший стовпець переставити на останнє місце, а інші стовпці пересунути вліво, зберігаючи їх порядок?
17. Як зміниться визначник, якщо кожний його елемент замінити елементом, симетричним з даним відносно «центру» визначника?
18. Як зміниться визначник порядку  , якщо у всіх його елементів змінити знак на протилежний?
, якщо у всіх його елементів змінити знак на протилежний?
19. Чому дорівнює визначник, у якого сума рядків з парними номерами дорівнює сумі рядків з непарними номерами?
20. Дано матрицю 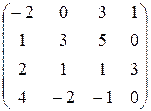 . Знайдіть:
. Знайдіть:
а) мінор  , що стоїть на перетині першого, другого та четвертого рядків, першого, третього та четвертого стовпців;
, що стоїть на перетині першого, другого та четвертого рядків, першого, третього та четвертого стовпців;
б) мінор, доповняльний до мінору  ;
;
в) алгебраїчне доповнення до мінору  .
.
21. Обчисліть визначники:
а)  , б)
, б) 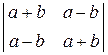 , в)
, в) 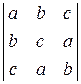 , г)
, г)  .
.
22. Використовуючи тільки властивості визначника, доведіть справедливість рівностей:
а)  ; б)
; б) 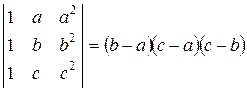 ;
;
в) 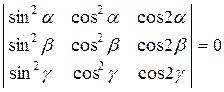 .
.
23. Користуючись властивостями визначника, обчисліть:
а) 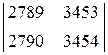 ; б)
; б)  ; в)
; в) 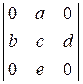 ; г)
; г) 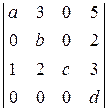 .
.
24. Розв’яжіть рівняння 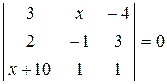 .
.
25. Розв’яжіть нерівність  .
.
26. Знайдіть всі члени визначника
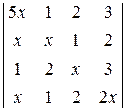 ,
,
що містять  и
и 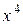 .
.
27. Розв’яжіть матричні рівняння з невідомою матрицею  в загальному вигляді:
в загальному вигляді:  ,
, 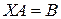 ,
, 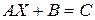 ,
, 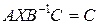 ,
, 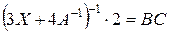 . Укажіть умови існування цих розв’язків.
. Укажіть умови існування цих розв’язків.
28. Знайдіть невідому матрицю  з рівняння:
з рівняння:
а)  ; б)
; б)  ;
;
в) 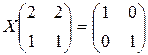 ;г)
;г) 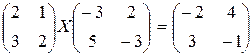 ;
;
д)  .
.
29. Як зміниться обернена матриця 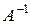 , якщо в матриці
, якщо в матриці 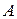 :
:
а) переставити 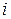 -ий та
-ий та  -ий рядки;
-ий рядки;
б)  -ий рядок помножити на число
-ий рядок помножити на число 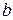 , відмінне від нуля;
, відмінне від нуля;
в) до  -ого рядка прибавити
-ого рядка прибавити 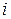 -ий, помножений на число
-ий, помножений на число 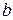 , відмінне від нуля?
, відмінне від нуля?
30. Запишіть систему двох рівнянь з двома невідомими, яка має нескінченно багато розв’язків (єдиний розв’язок).
31. Запишіть систему з найменшим числом невідомих, що має більше невідомих, ніж рівнянь, але не має розв’язків.
32. При яком значенні 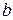 сумісна система
сумісна система

|
|
|
|
|
Дата добавления: 2014-12-17; Просмотров: 538; Нарушение авторских прав?; Мы поможем в написании вашей работы!