Завдання для самостійного опрацювання

1. Знайдіть значення визначника -го порядку методом рекурентних співвідношень:

а) 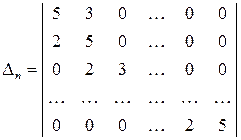; б) .

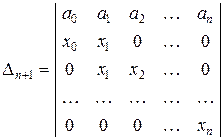Розв’язання:

Метод рекурентних співвідношень полягає в наступному: розкладанням за рядком або стовпцем даний визначник виражають через визначники такого ж виду, але меншого порядку. Отримана рівність називається рекурентним співвідношенням.

Для отримання значення визначника довільного порядку, обчисливши з рекурентного співвідношення декілька визначників менших порядків, намагаються «вгадати» загальний вираз шуканого виразу, а потім доводять його справедливість методом математичної індукції.

а) Розглянемо один з частинних випадків, коли рекурентне співвідношення дає алгоритм для розв’язання задачі, що виключає елемент здогадки.

Нехай рекурентне співвідношення має вид

,

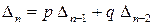де 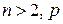и 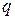не залежать від ; 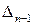, 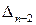– визначники матриць 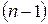-ого, 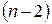-ого порядків такого ж виду. Розглянемо два випадки:

1) при ;

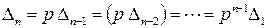2) при 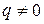складаємо квадратне рівняння 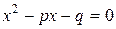, коренями якого є числ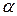а та :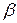

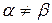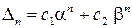а) якщо , то , де

;

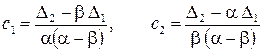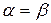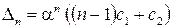б) якщо , то , де

.

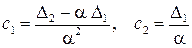Проілюструємо наведений алгоритм на прикладі, але спочатку знайдемо значення визначників цього типу першого – четвертого порядків:

, ,

,

.

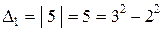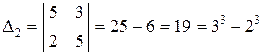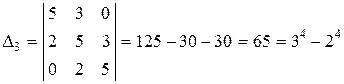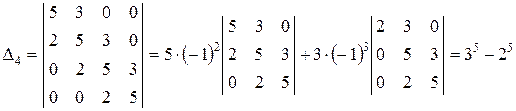Тепер розглянемо визначник -ого порядку. Спочатку розкладемо його за першим рядком:

.

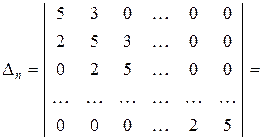
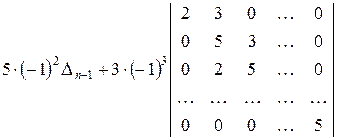Тут 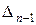– визначник такого же виду, що й вихідний, але 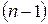–ого порядку. Останній визначник в отриманому представленні 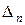розкладемо за першим стовпцем:

.

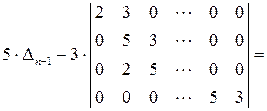
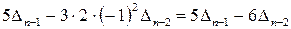Таким чином, приходимо до співвідношення .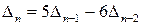

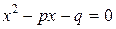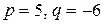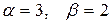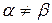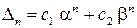Складемо квадратне рівняння виду , де . Коренями його будуть числа . Так як , то , де

.

За знайденими значеннями 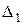, 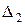визначаємо: 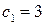, 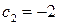. Отже, .

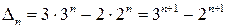б) Розглянемо визначники менших порядків для з’ясування приблизної форми визначника 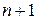-ого порядку:

, ,

,

.

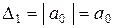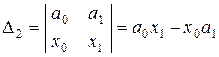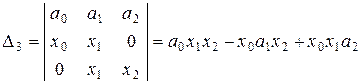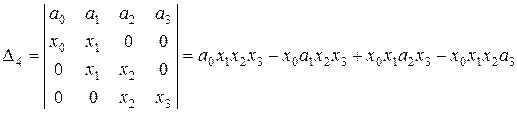На основі цих записів можна припустити, що

.

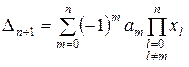Доведемо правдивість цієї формули методом математичної індукції. При 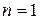твердження істинне. Припустимо, що при 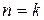: 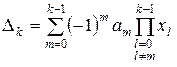. Доведемо, що при 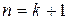: 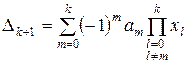. Для цього розкладемо вихідний визначник за останнім стовпцем:

.

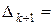
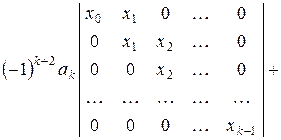
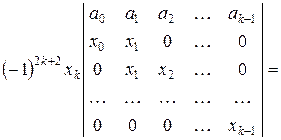
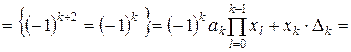
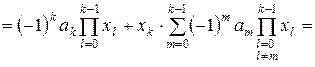
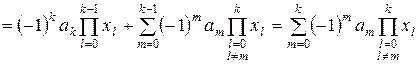Що і треба було довести.

2. Обчисліть значення визначника, що зводиться до визначника Вандермонда:

, , , .

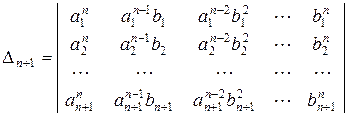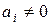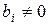Розв’язання:

Визначником Вандермонда називається визначник виду:

.

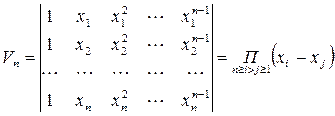Зведемо даний в умові визначник до визначника такого типу наступним чином: винесемо з першого рядка множник 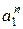, з другого – 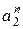, , 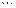з останнього – . Отримаємо:

.

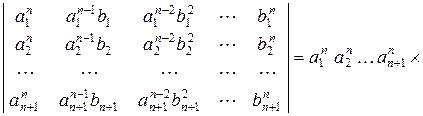
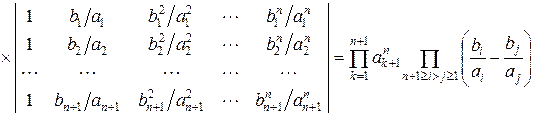3. Обчисліть визначники -го порядку:

а) 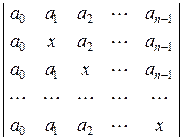, б) .

Розв’язання:

а) Зведемо матрицю до трикутного виду, для чого віднімемо від кожного її рядка перший рядок. Тоді

.

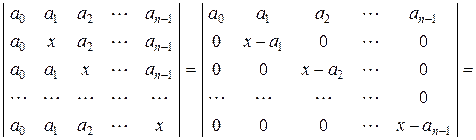
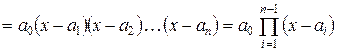б) Перевіряючи отримані знання, читач може впевнитись самостійно, що:

.

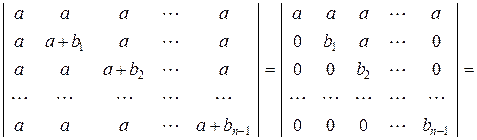
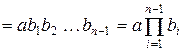Дата добавления: 2014-12-17