
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Для самостійного розв’язування
|
|
|
|
ДОДАТКОВІ ЗАВДАННЯ
1. Укажіть транспозиції, за допомогою яких можна перейти від перестановки:
1)  до перестановки
до перестановки  ;
;
2)  до перестановки
до перестановки 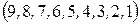 .
.
2. Знайдіть число інверсій у наступних перестановках та визначте їх парність:
1)  ; 2)
; 2)  .
.
3. Знайдіть число інверсій в перестановках та укажіть загальний вигляд тих  , для яких перестановка буде парною, та тих
, для яких перестановка буде парною, та тих  , для яких вона буде непарною:
, для яких вона буде непарною:
1)  ;
;
2)  ;
;
3)  ;
;
4) 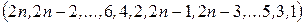 .
.
4. З’ясуйте, які з наведених добутків є членами визначника відповідного порядку. У випадку позитивної відповіді визначте його знак:
1)  ; 2)
; 2)  ; 3)
; 3)  .
.
5. Оберіть 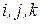 таким чином, щоб наступні добутки були додатними членами визначників відповідних порядків:
таким чином, щоб наступні добутки були додатними членами визначників відповідних порядків:
1) 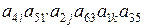 ; 2)
; 2)  .
.
6. Обчисліть визначники:
1) 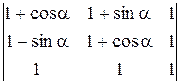 ; 2)
; 2)  ; 3)
; 3) 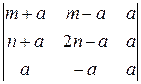
7. Знайдіть розв’язки рівняння.
1)  ; 2)
; 2)  ; 3)
; 3)  ;
;
4)  , 5)
, 5) 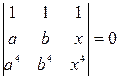 .
.
8. При яких значеннях k система

сумісна?
9. При яких значеннях t система

має ненульові розв’язки?
10. Числа 204, 527 і 255 діляться на 17. Доведіть, що визначник  також ділиться на 17.
також ділиться на 17.
11. Обчисліть визначник
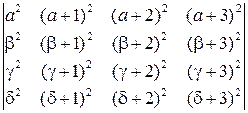 .
.
12. Доведіть справедливість наступних рівностей:
1)  ;
;
2)  .
.
13. Розкладіть за елементами третього рядка і обчислити визначник
 .
.
14. Розкладіть за елементами останнього стовпця і обчислити визначник
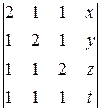 .
.
15. Розкладіть за елементами першого стовпця і обчислити визначник
 .
.
16. Обчисліть визначники:
1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4) 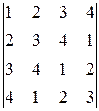 ;
;
5)  ; 6)
; 6) 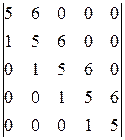 ; 7)
; 7)  ;
;
8)  .
.
17. Розв’яжіть за формулами Крамера системи рівнянь:
1)  2)
2)  3)
3) 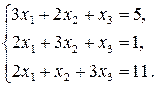
4) 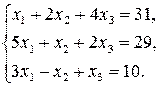 5)
5) 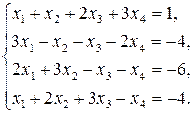 6)
6) 
7)  8)
8) 
9)  10)
10) 
11)  12)
12) 
18. Доведіть, що система

має єдиний розв’язок, якщо a, b, c, d — дійсні числа, серед яких не всі дорівнюють нулю.
19. Скільки визначників k -го порядку можна скласти з матриці, що має m рядків і n стовпців?
20. Складіть матрицю, ранг якої дорівнює: а) 2; б) 3.
21. Доведіть, що ранг суми двох матриць не перевищує суми рангів матриць-доданків.
22. Як може змінитися ранг матриці, якщо до неї дописати:
а) 1 стовпець, б) 2 стовпці?
23. Обчисліть ранг матриці:
1) 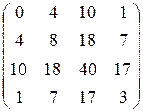 . 2)
. 2)  .
.
3) 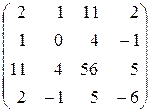 . 4)
. 4)  .
.
5)  . 6)
. 6)  .
.
7)  . 8)
. 8) 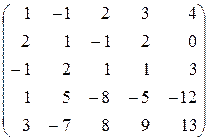 . 9)
. 9)  .
.
10)  . 11)
. 11)  .
.
12)  . 13)
. 13) 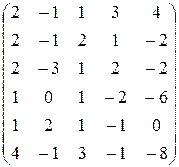 .
.
24. Розв’яжіть системи рівнянь:
1)  2)
2)  3)
3) 
4)  5)
5) 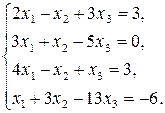 6)
6) 
7) 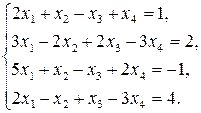 8)
8) 
9) 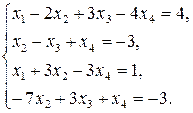 10)
10) 
11)  12)
12) 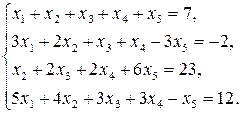
13) 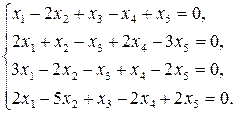 14)
14) 
15) 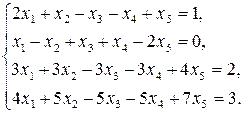 16)
16) 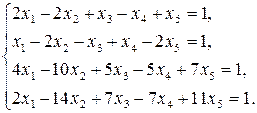
17)  18)
18) 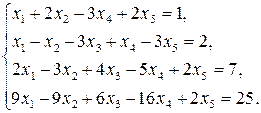
25. Система

має єдиний розв’язок. Доведіть, що  , і знайдіть розв’язок.
, і знайдіть розв’язок.
26. Розв’яжіть систему рівнянь в залежності від параметру:
1) 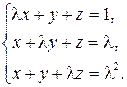 2)
2) 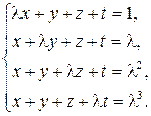 3)
3) 
4)  5)
5)  6)
6) 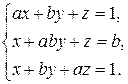
7) 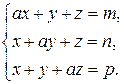 8)
8)  9)
9) 
27. Чи є матриця 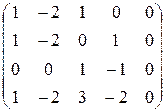 фундаментальною системою розв’язків системи рівнянь
фундаментальною системою розв’язків системи рівнянь
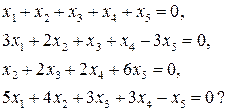
28. Знайдіть добутки матриць:
1)  ; 2)
; 2)  ; 3)
; 3) 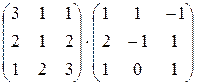 ;
;
4)  ; 5)
; 5)  .
.
29. Виконати дії:
1)  ; 2)
; 2) 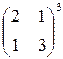 ; 3)
; 3)  ; 4)
; 4) 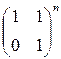 ; 5)
; 5)  .
.
30. Доведіть, що кожна матриця другого порядку  задовольняє рівняння
задовольняє рівняння 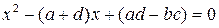 .
.
31. Знайдіть всі матриці другого порядку, квадрати яких дорівнюють нульовій матриці.
32. Знайдіть всі матриці другого порядку, куби яких дорівнюють нульовій матриці.
33. Знайдіть всі матриці другого порядку, квадрати яких дорівнюють одиничній матриці.
34. Розв’яжіть і дослідіть рівняння 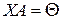 , де
, де 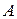 – деяка відома матриця, а
– деяка відома матриця, а  – шукана матриця другого порядку.
– шукана матриця другого порядку.
35. Розв’яжіть і дослідіть рівняння 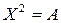 , де
, де 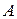 – деяка відома матриця, а
– деяка відома матриця, а  – шукана матриця другого порядку.
– шукана матриця другого порядку.
36. Знайдіть обернену матрицю для матриці А.
1) 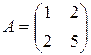 ; 2)
; 2)  ; 3)
; 3) 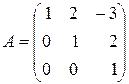 ; 4)
; 4) 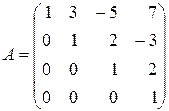 ;
;
5)  ; 6)
; 6) 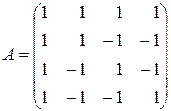 ; 7)
; 7) 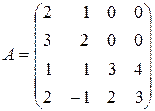 .
.
37. Знайдіть невідому матрицю  з рівняння:
з рівняння:
1)  ; 2)
; 2) 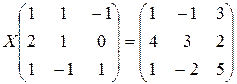 ; 3)
; 3) 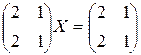 ;
;
4) 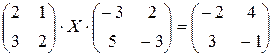 ; 5)
; 5) 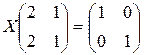 .
.
38. Обчисліть  , де
, де  ,
, 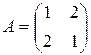 .
.
39. Знайдіть всі дійсні матриці другого порядку, куби яких дорівнюють одиничній матриці.
40. Знайдіть всі дійсні матриці другого порядку, четверті степені яких дорівнюють одиничній матриці.
41. Доведіть, що
1)  ;
;
2) 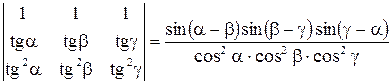 .
.
42. Обчисліть  , якщо
, якщо
 ,
, 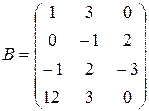 ,
, 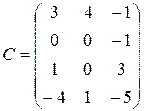 .
.
43. Обчисліть  , якщо
, якщо
 ,
,  ,
,  .
.
44. При яких значеннях  система рівнянь не сумісна, сумісна? У випадку сумісності укажіть кількість розв’язків СЛАР:
система рівнянь не сумісна, сумісна? У випадку сумісності укажіть кількість розв’язків СЛАР:
1) 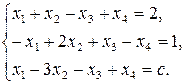 2)
2) 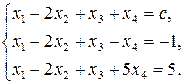
3) 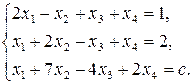 4)
4) 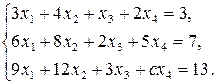
5)  6)
6) 
45. Знайдіть загальний розв’язок та ФСР однорідної СЛАР:
1)  2)
2) 
3)  4)
4) 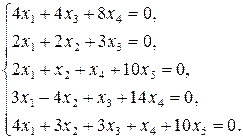
46. Користуючись теоремою Лапласа, знайдіть значення визначників:
1) 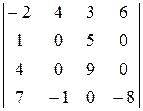 ; 2)
; 2) 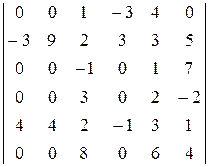 ; 3)
; 3) 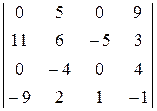 ;
;
4)  ; 5)
; 5) 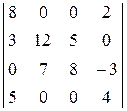 ; 6)
; 6)  .
.
47. Знайдіть значення визначників  -го порядку методом рекурентних співвідношень.
-го порядку методом рекурентних співвідношень.
1)  ; 2)
; 2)  ;
;
3) 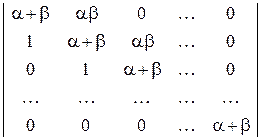 ; 4)
; 4) 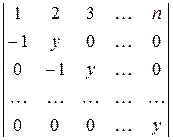 .
.
48. Обчисліть значення визначників, що зводяться до визначника Вандермонда.
1)  ; 2)
; 2) 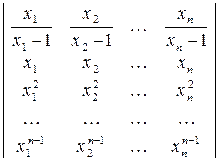 ;
;
3) 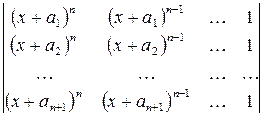 ; 4)
; 4) 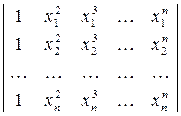 .
.
49. Обчисліть визначники  -го порядку:
-го порядку:
1)  ; 2)
; 2)  ;
;
3) 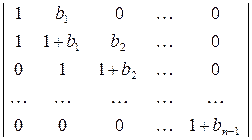 ; 4)
; 4) 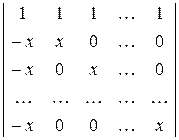 .
.
ПИТАННЯ ДЛЯ САМОКОНТРОЛЮ
1. Поняття n -вимірного рядка. Поняття матриці. Квадратна, прямокутна, нульова, одинична, верхньотрикутна, нижньотрикутна, діагональна матриці.
2. Додавання матриць та його властивості.
3. Добуток числа та матриці, його властивості.
4. Правило добутку двох матриць.
5. Транспонування матриць та його властивості. Обернена матриця. Методи знаходження матриці, оберненої даній.
6. Елементарні перетворення рядків матриці. Ступінчаста матриця. Зведення матриці до ступінчастого виду за допомогою елементарних перетворень рядків.
7. Ранг матриці.
8. Лінійне алгебраїчне рівняння. Системи рівнянь. Розв’язок системи. Однорідні, неоднорідні, сумісні, несумісні, означені, неозначені системи. Еквівалентні системи. Приклади.
9. Типи відображень множин. Підстановки та перестановки.
10. Поняття та властивості визначника n -го порядку.
11. Мінори та алгебраїчні доповнення. Теорема про розкладання визначника за елементами рядку або стовпчика.
12. Формули Крамера розв’язання СЛАР.
13. Теорема Кронекера-Капеллі дослідження матриці на сумісність.
14. Метод Гауса розв’язання СЛАР.
15. Загальний розв’язок системи, частинний розв’язок системи.
16. Матричний метод розв’язання СЛАР.
17. Однорідні системи. Достатня умова існування нетривіального розв’язку.
18. Фундаментальна система розв’язків та її побудова.
|
|
|
|
|
Дата добавления: 2014-12-17; Просмотров: 753; Нарушение авторских прав?; Мы поможем в написании вашей работы!