Аналитическая геометрия

Выберем в пространстве две упорядоченные точки А и В. Соответствующий направленный отрезок называется вектором.

Расстояние между точками А и В называется модулем или длиной вектора. Для модуля вектора используются обозначения , а. Вектор называется единичным вектором, если 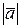= 1.

Несколько векторов называются коллинеарными, если все они расположены на прямых, параллельных одной и той же прямой. Если векторы и коллинеарны, то записывают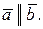

Несколько векторов называются компланарными, если существует плоскость, параллельная всем прямым, на которых эти векторы расположены.

Составим суммы векторов, умноженных на числа

Выражения такого вида называются линейными комбинациями векторов.

Если некоторый вектор представлен в виде линейной комбинации каких-либо векторов, то говорят, что он разложен по этим векторам.

Базисом в пространстве называют любые три упорядоченных некомпланарных вектора. При этом любой вектор пространства является их линейной комбинацией.

Если () – базис в пространстве, то любой вектор

при этом числа 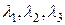называются координатами вектора в базисе (). Записывают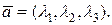

Выберем в пространстве точку О и возьмем упорядоченную тройку ортогональных единичных векторов () – базис в пространстве.

Совокупность точки О и базиса () называется ортогональной декартовой системой координат. При этом принята следующая терминология: О – начало координат; прямые, проходящие через начало в направлении базисных векторов – оси координат; плоскости, проходящие через оси координат – координатные плоскости. На рисунке 2.1 показана правая система координат.

Если А (х ₁, у ₁, z ₁), B (х ₂, у ₂, z ₂) – точки, заданные в декартовой системе координат, то координаты и модуль вектора можно найти по формулам

, (2.1)

. (2.2)

Скалярным произведением двух векторов называется число, равное произведению модулей векторов, умноженному на косинус угла между векторами

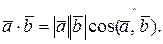
Если векторы заданы координатами, то скалярное произведение вычисляется по формуле

(2.3)

С помощью скалярного произведения можно найти угол между векторами через их координаты:

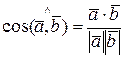. (2.4)

Векторным произведением вектора на вектор называется вектор , модуль которого равен площади параллелограмма, построенного на векторах и , а направление ортогонально к векторам и , причем векторы () образуют правую тройку векторов (см. рисунок 2.2).

.

Обозначается векторное произведение .

Если векторы заданы координатами, то векторное произведение находят по формуле

. (2.5)

С помощью векторного произведения можно вычислить площадь треугольника , где , – векторы, на которых построен треугольник.

Смешанное произведение трех векторов определяется следующим образом:

Модуль смешанного произведения выражает объем параллелепипеда, построенного на перемножаемых векторах.

Если известны координаты векторов, то

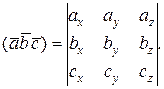(2.6)

Линейное уравнение вида

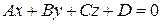(2.7)

называется общим уравнением плоскости.

Вектор , составленный из коэффициентов при x, y, z, направлен по нормали к плоскости (2.7) и называется нормальным вектором плоскости.

Уравнение плоскости, проходящей через данную точку М (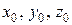) и перпендикулярной вектору , имеет вид

.

Уравнение плоскости, проходящей через три точки 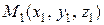, , 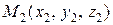, 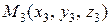не лежащие на одной прямой, имеет вид

. (2.8)

Канонические уравнения прямой линии имеют вид

Здесь - некоторая фиксированная точка, принадлежащая данной прямой; 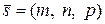- направляющий вектор прямой, т.е. вектор, лежащий на прямой, параллельной данной.

Уравнение прямой, проходящей через две точки 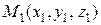, , имеет вид

. (2.9)

Если точки A (x ₁, y ₁, z ₁), B (x ₂, y ₂, z ₂) и M (x, y, z) лежат на одной прямой и , то координаты точки M можно найти по формулам

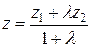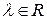; ; , . (2.10)

Общее уравнение прямой на плоскости имеет вид

,

причем хотя бы один из коэффициентов отличен от нуля.

Ненулевой вектор = (А, В), перпендикулярный к данной прямой, называется нормальным вектором прямой на плоскости.

Уравнение прямой на плоскости с угловым коэффициентом k имеетвид

y = kx + b (k = tgj, где j – угол наклона прямой к оси Oх).

Условия параллельности и перпендикулярности двух прямых с угловыми коэффициентами k ₁ и k ₂ определяются соответственно равенствами

k ₁ = k ₂, k ₁ = –1 / k ₂.

Уравнение прямой, проходящей через точку М (х ₀, у ₀), параллельно данной прямой y = k ₂ x + b имеет вид

. (2.11)

Уравнение прямой, проходящей через точку М (х ₀, у ₀), перпендикулярно данной прямой y = k ₁ x + b имеет вид

. (2.12)

Расстояние d от точки M (x ₀, y ₀) до прямой Ах + Ву + С = 0 определяется по формуле

. (2.13)

Дата добавления: 2014-12-17