Правила дифференцирования. Определение. Пусть функция y = f(x) определена в точке x0 и некоторой её окрестности, x – произвольная точка этой окрестности

ПРОИЗВОДНАЯ ФУНКЦИИ

Определение. Пусть функция y = f(x) определена в точке x₀ и некоторой её окрестности, x – произвольная точка этой окрестности. Если существует конечный предел отношения 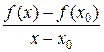при x → x₀ , то этот предел называется производной функции y = f(x) в точке x₀ и обозначается 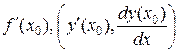. Итак,

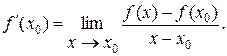
Обозначив через 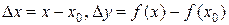, получим

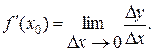
Операция нахождения производной называется дифференцированием функции. Дифференцируемость функции в точке (на промежутке) равносильна наличию у функции конечной производной в этой точке (в каждой точке промежутка).

Геометрический смысл производной: если функция y = f(x) дифференцируема в точке x₀ , то график этой функции имеет касательную в точке 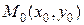и угловой коэффициент касательной равен 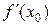, т. е. 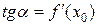, где 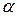– угол наклона касательной к оси Оx.

На интерпретации производной, как величины скорости изменения одной величины y относительно другой x, основано применение производной в физике, технике и др.

Если С – постоянное число, u = u(x) и υ = υ(x) – дифференцируемые функции, то справедливы следующие правила дифференцирования:

1. ;	3. 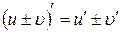;	5. ;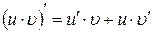
2. 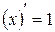;	4. 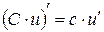;	6. .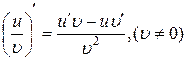
7. Пусть функция y = f(x) определена, непрерывна и дифференцируема в точке x0. Тогда обратная функция 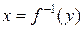имеет производную в точке y0 = f(x0) и .
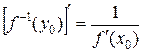8. Если сложная функция y=f(φ(x)) составлена из дифференцируемых функций y = f(u), u = φ(x), то сложная функция дифференцируема 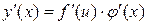и или .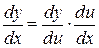

Таблица производных основных элементарных функций

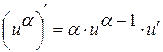
1.	2.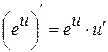
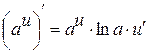
3.	4.
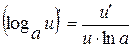
5.	6.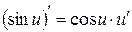
7.	8.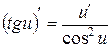
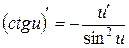
9.	10.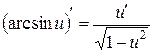
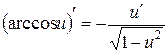
11.	12.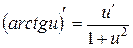
13. .

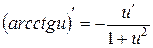Определение. Дифференциалом первого порядка dy функции y = f(x) называется главная часть её приращения Δy, линейно зависящая от приращения Δx независимой переменной x. Дифференциал может быть вычислен по формуле

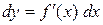
в любом случае: будет ли x независимой переменной или нет (свойство инвариантности формы первого дифференциала).

Определение. Производной второго порядка (второй производной) функции y = f(x) называется производная от её первой производной (если она существует): .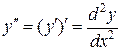

Соответственно производная n-го порядка равна: .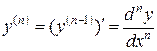

Если функция y = y(x) задана параметрически системой уравнений

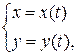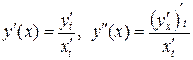то , или .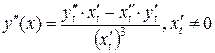

Способы отыскания пределов отношений бесконечно малых или бесконечно больших дифференцируемых функций с помощью производных носят общее название правила Лопиталя: предел отношения таких функций заменяется пределом отношения их производных, если последний существует, т. е.

.

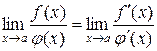Применяется для раскрытия неопределенностей вида 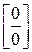или 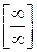. Неопределенности вида 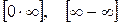следует предварительно приводить к одному из первых двух видов. Правило Лопиталя можно применять несколько раз.

Дата добавления: 2014-12-17