Решение дифференциальных уравнений. Графическое отображение данных

Графическое отображение данных

Построение графиков в Scilab производится с помощью функции plot. Функция имеет следующий синтаксис:

plot(x,y)

Т.к. функция строит график по точкам, необходимо предварительно определить координаты точек. Для этого создаём переменную в виде вектора со значениями диапазона построения. Определяем вектор значений по оси ординат и строим график:

-->x = -2*%pi:0.1:2*%pi; -->y = sin(2*x); -->plot(x,y)

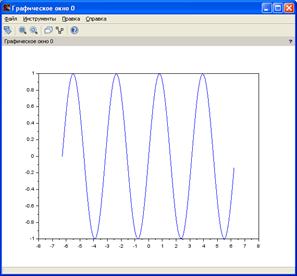
Для того, чтобы отобразить несколько графиков на одном холсте, необходимо создать вектор, столбцы которого будут являться новыми линиями на графике:

-->x = -%pi:0.1:%pi; -->plot(x,[sin(2*x); sin(x); 2*sin(x)])

Для решения дифференциальных уравнений и систем в Scilab предусмотрена функция

[y,w,iw]=ode(y0,t0,t,f)

для которой обязательными входными параметрами являются: y0 – вектор начальных условий; t0 —начальная точка интервала интегрирования; t – координаты узлов сетки, в которых происходит поиск решения; f – внешняя функция, определяющая правую часть уравнения или системы уравнений; y – вектор решений.

Таким образом, для того чтобы решить обыкновенное дифференциальное уравнение вида , необходимо вызвать функцию

y=ode(y0,t0,t,f).

где, f – ссылка на предварительно созданную функцию f(t; x);

t – координаты сетки;

x0, t0 – начальное условие x(0) = 1:5;

y – результат работы функции.

Дата добавления: 2014-12-17