Они приходят порциями, и вероятностьих попа­дания складывается без интерференции. 2 страница

Сводка выводов:

1. Вероятность события в идеальном опыте дается квадратом абсолютной величины комплексного числа j, называемого амплитудой вероятности. Р – вероятность, j – амплитуда вероятности,

Р = ½ j ½². (6')

2. Если событие может произойти несколькими вза­имно исключающими способами, то амплитуда вероят­ности события ¾ это сумма амплитуд вероятностей ка­ждого отдельногоспособа. Возникает интерференция:

j = j₁ + j₂. (7')

P = ½ j₁ + j₂ ½².

3. Если ставится опыт, позволяющий узнать, какой из этих взаимно исключающих способов на самом деле осуществляется, то вероятность события ¾ это сумма вероятностей каждого отдельного способа. Интерферен­ция отсутствует.

Р = Р₁ + Р₂. (8¢)

Быть может, вам все еще хочется выяснить: «А Поче­му это? Какой механизм прячется за этим_: законом?» Так вот: никому никакого механизма отыскать не уда­лось. Никто в мире не сможет вам «объяснить» ни на капельку больше того, что «объяснили» мы. Никто не даст вам никакого более глубокого представления о по­ложении вещей. У нас их нет, нет представлений о бо­лее фундаментальной механике, из которой можно вы­вести эти результаты.

Мы хотели бы подчеркнуть очень важное различие между классической и квантовой механикой. Мы уже говорили о вероятности того, что электронпопадает туда-то и туда-то в данных обстоятельствах. Мы подразумевали, что с нашим (да и с самым лучшим) экспериментальным устройством невозможно будет предсказывать точно, что произойдет. Мы способны только определять шансы! Это означало бы, если это утверждение правильно, что физика отказалась от попытки предсказывать точно, что произойдет в оп­ределенных условиях. Да. Физика и впрямь сдалась. Мы не умеем предсказывать, что должно было бы слу­читься при данных обстоятельствах.

Мало того, мы уверены, что это немыслимо: единст­венное, что поддается предвычислению, это вероят­ность различных событий; Приходится признать, что мы изменили нашим прежним идеалам понимания при­роды. Может быть, это шаг назад, но никто не научил нас, как избежать его!

Сделаем теперь несколько замечаний об одном ут­верждении, которое иногда делали те, кто не хотел пользоваться приведенным описанием. Они говорили: «Может быть, в электроне происходят какие-то внут­ренние процессы, имеются какие то внутренние переменные, о чём мы пока ничего не знаем (т.e. на про­странственное перемещение электрона может воздействовать некоторые внутренние или внешние скрытые параметры. - А.Ч.).Может быть, именно по­этому мы не умеем предугадывать, что случится. А если бы мы могли пристальнее вглядеться в электрон, то смогли бы сказать, куда он придет».

Насколько нам известно, такой возможности нет. Трудностивсе равно остаются. Предположим, что внутри электрона есть механизм какого-то рода, опре­деляющий, куда электрон собирается попасть. Тогда эта машина должна определить также, через какое от­верстие он намерен проследовать. Но не забывайте, что вся эта внутри электронная механика не должна зависеть от того, что делаем мы, и, в частности, от того, открыли мы данное отверстие или нет. Значит, если электрон, отправляясь в путь, уже прикинул, сквозь какую дырку он протиснется и где он при­землится, то для электронов, облюбовавших отверстие 1, мы получим распределение P₁, а для остальных ¾ распределение Р₂. А тогда для тех электронов, которые прошли через оба отверстия, с необходимостью рас­пределение окажется суммой P₁ + P₂. Не видно способа обойти этот вывод. Но мы экспериментально доказали, что он неверен. Никто еще не нашел отгадки этой голо­воломки. Стало быть, в настоящее время приходится ограничиваться расчетом вероятностей. Мы говорим «в настоящее время», но мы очень серьезно подозреваем, что все это ¾ уже навсегда, и разгрызть этот орешек человеку не по зубам, ибо такова природа вещей».

Данная, хотя и очень длинная, цитата достаточно красноречиво фиксирует растерянность крупного физи­ка-теоретика перед объективными загадками микроми­ра. Вот она плата за нарушение законов природы, целая фантастическая наука ¾ квантовая механика.

Ниже будет показано, что «природа вещей» несколь­ко отличается от той, которую очень пространно опи­сывает Фейнман. И хотя он стремится показать, что другой картины при прохождении электрона через две щели быть не может, объяснение сопровождается таким количеством оговорок о том, что «никто еще не нашел отгадки этой головоломки», что поневоле создается впечатление, что и он, сделавший, независимо от своего желания, очень многое для дальнейшего запутывания природы квантовых явлений, сомневается в оконча­тельной истинности предлагаемых объяснений. Более того, эти оговорки свидетельствует о его некотором по­нимании наличия внутренней противоречивости кван­товой механики и о том, что он, похоже, присоединяет­ся к тем выдающимся физикам, которые считали ее слабо обоснованной и алогичной. Некоторая уверен­ность Фейнмана базировалась еще и на том, что была доказана математиком фон Нейманом теорема об отсут­ствии в квантовой механике скрытых параметров, и не было известно внешнего по отношению к квантовой механике логического или математического аппарата, способного отслеживать возникнове-ние неувязок в ее решениях.

Возможность существования скрытых параметров дискутировалась с самого возникновения квантовой механики. Большинство физиков (после доказательства фон Неймана) уверовали в их отсутствие. Возможность наличия скрытых параметров отрицается не потому, что их нет и не может быть (это самоуверенность утвер­ждать, что все бесчисленные свойства природы нам из­вестны) и не потому, что их невозможно найти (допус­тим, не хватает способностей у человека или слаба экспериментальная база), а потому, что наличие таких параметров противоречит замкнутой логике кванто­вой механики.

Но «скрытые параметры» могут вообще ни от кого не скрываться. Можно ли считать скрытым параметром массу электрона? Или его заряд? Или постоянную Ридберга? Ведь они входят в квантовую механику, но вхо­дят как величины неизменные, а потому их изменяе­мость оказывается скрытым параметром. А вот наличие вещественного эфира, запрещенного ОТО, но от этого не исчезнувшего в природе проводника всех видов взаи­модействий и самопульсации тел действительно мож­но считать скрытым параметром. И именно их отсут­ствие в квантовой механике превращает эту механику в замкнутую систему, в систему, образуемую нескольки­ми «закольцован-ными» свойствами и неспособную к расширению, к корректному описанию всех микроявле­ний.

Возможность самопульсации пространства, тел и элементарных частиц без подвода энергии (механизм, которого не только неизвестен, но даже и не предпола­гается) противоречит логике уже классической механи­ки. И потому, как полагают ученые, не может сущест­вовать никакая самопульсация, никакой связанный с ней скрытый параметр. Вот основная причина отсутст­вия объективного объяснения эксперимента по прохож­дению электрона через два отверстия. Чтобы понять квантовые явления, нужно «перешагнуть» через эту ло­гику, отказаться от нее и признать наличие самопульса­ции атрибутом существования всех тел.

Самопульсация всех тел, существование структури­рованного эфира и изменение массы и заряда элемен­тарных частиц — те скрытые параметры, отсутствие представления о которых и явилось основой поро­ждения квантовых постулатов (законов). Еслисуще­ствует самопульсация, то электрон движется по орбите за счет взаимодействия с окружающим эфирным про­странством, расходуя на свое движение ровно такое ко­личество энергии, которое он получает непонятным (пока) образом. Тогда вопрос о самостоятельности вол­новых свойств, их антагонизма свойствам корпускуляр­ным снимается. Становится возможным рассмотрение квантовых взаимодействий по законам, принципиально отличающимся от принятых законов квантовой механи­ки ¾ по законам макромира.

Если же электрон на свое движение расходует энер­гию, то отпадает необходимость в постулировании стационарных орбит и в целочисленном квантовании. Это не значит, что отсутствуют квантовые скачки, но это означает, что механизм и физика квантовых явлений нами понимаются и описываются некорректно. Именно неадекватное природе описание квантовых явлений становится главным фактором непонимания механиз­ма квантования, математической формализации физи­ческих процессов микромира и широкой интуитивной оппозиции многих великих физиков (включая А. Эйн­штейна, А. Лоренца, Де Бройля, П. Дирака, Э. Шредингера и др.) онтологии квантования.

Вернемся к объяснению движения электрона через две щели. Естественно, что появление даже одного скрытого параметра, тем более такого, который обу­словливает механизм движения тела в пространстве, автоматически изменяет представление о физике про­странства и, следовательно, ставит под вопрос теоре­тическую надежность квантовой механики. Скрытыми параметрами, движением взаимодействия отрицается не только движение электрона по инерции, отрицается также существование пустого пространства. В резуль­тате этих отрицаний электрон (как и любое другое «элементарное» тело) как бы наделяется принципиально новым свойством (кстати, хорошо известным в совре­менной физике) — «выбирать» траекторию движения в пространстве по кратчайшему пути, тому пути,который обеспечивает наименьшую деформацию электрону при следовании по нему (этой деформации и не замечет Р. Фейнман. Более того, он отрицает саму возможность деформации заявляя, что «внутри электронная механика не должна зависеть от того, что делаем мы и, в частности, от того, открыли мы от­верстие или нет»). И главное, что происходит в экспе­рименте с двумя щелями, заключается в том, что от­ крытие или закрытие щели изменяет плотность пространства перед щелью и за ней. Измененная плотность пространства, воздействуя на движу­щийся электрон (деформируя его), изменяет траек­торию его движения, создавая на экране тот или другой рисунок детектирования результатов. Пока­жусхему попадания электронов в щели (рис. 65), но предварительно отмечу и другие факторы, влияющие на их поведение (другие скрытые параметры).

При моделировании с двумя щелями неявно предпо­лагается, что перегородка не материальна и не дефор­мирует пространство перед собой, само пространство пусто по определению (т.е. невещественно и не облада­ет волновыми свойствами). Электрон (не тело) — заряд постоянной величины, летящий по инерции по прямой и, следовательно, без взаимодействия с пространством. Все электроны летят с одной скоростью, тождественны друг другу (т.е. аналогичны пулям) обладают корпускулярно-волновыми свойствами (тоже невещественны). Пространство щелей пусто, тел и полей не вмещает, за­крытие одной из щелей не вносит никаких деформаций в пространство соседней щели. Электрон, не попавший в отверстие щели, а ударивший в перегородку или в простенок, по инерции отлетает в сторону. Испускатель электронов находится строго на оси простенка, а кон­фигурация от электронов на экране пропорциональна расстоянию от него до перегородки. Вот те дополни­тельные факторы, которые вносят свою лепту в пони­мание взаимодействия электрона с перегородкой с дву­мя щелями.

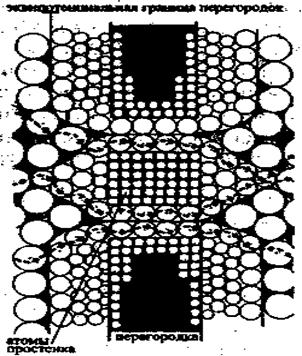
Рис. 65.

Не обсуждая подробности самого эксперимента с движением электронов через отверстия перегородки, покажу, что представляет собой пространство в окрест­ностях перегородки с двумя открытыми щелями (рис. 65), а также с одной закрытой щелью (рис. 66). И станет понятно, как будет двигаться электрон при двух открытых щелях, попадая даже в середину простенка.

На рис 65 с левой стороны молекулы эфира, через ко­торые пролетает электрон на пути к перегородке, справа ¾ молекулы перегородки, а за ней снова до экрана про­странство эфира. Его траектория определяется той скоростью, которая была придана ему импульсом от­рыва (разгоном) от излучателя. Скорость отрыва обу­словливает электрону движение в атомах и молекулах строго по определенной траектории и вход в эквипо­тенциальную поверхность молекул перегородки под со­ответствующим углом (рис. 65). Движение в эквипо­тенциальной зоне молекул пульсирующей перегородки будет проходить в промежутках между пучностями, что и обеспечивает электрону возможность выхода из зоны действия этих молекул на некотором как бы квантованном пучностями расстоянии от электронов, имеющих даже незначительное отличие от него в скорости. Эти незначи­тельные отличия приводят к тому, что электроны «входят» в эквипотенциальное про­странство молекулы под раз­личными углами, двигаются в этом пространстве по различ­ным узлам и выходят за пере­городкой из различных точек ее эквипотенциального про­странства. Вот тот процесс, который и вызывает появле­ние интерференции на экране.

Наличие двух щелей в перегородке качественно меня­ет картину движения электрона. Надо помнить, что расстояние между щелями по порядку величины не может быть больше длины волны электрона, а это значит, что эквипотенциаль-ные поверхности щелей и простенка перекрываются, а собственная пульсация простенка усиливает стоячие волны в обеих щелях, что приводит к более четкому разделению электронов в пространстве щелей и в их движении к экрану. К тому же перегородка образует в направлении излучателя не­которую выпуклость (рис. 65), оканчивающуюся «сред­ним» атомом, как раз имеющим радиус примерно рав­ный половине волны электрона. Электроны, «налетающие» на этот атом ниже или выше его ядра (по рис. 65), будут «направляться» (модулироваться) эквипотенциальным полем атома либо в одну, либо в дру­гую щель. На выходе из щели он отрывается от послед­него атома перегородки под несколько большем углом, чем тот, под которым входил в пространство первого атома. Вот те обстоятельства, которые обусловливают появление на экране интерференционной картины.

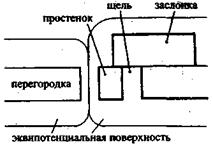
При одной открытой щели модулятор отключается «заслонкой» (рис. 66), и эквипотенциальная поверх­ность от стенок щели к ее центру изменяется примерно одинаково (т.е. структура пространства вокруг щели изменяется, становясь такой же, как и при одной щели), электроны, попадая в одинаковые условия перед ще­лью, распределяются за перегородкой тоже примерно одинаково, большая часть из них сосредотачивается на­против центра щели, так как напряжен-ность поля там наименьшая.

Рис. 66

Поскольку при закрытии одной щели «выпуклость» модулятора перед пе­регородкой и за ней исчезает («погашают­ся» плотностью за­слонки), то исчезают и условия, обеспечи­вающие моду- лирова­ние электронов по эк­рану, а вместе с ними прекращается процесс интерференции.

Несколько слов о мысленном «пулемете» Р. Фейнмана. Именно модель «пулемета» как прообраза, сопос­тавляемого с квантовой моделью, наглядно показывает те нюансы, которые были упущены при выдвижении квантовой гипотезы. Чтобы модель «пулемета» кор­ректно соответствовала квантовой модели с щелью или двумя щелями, перегородка с отверстиями для пролета пуль должна быть сделана по толщине из десятков тел радиусом, равным радиусу Земли. Тела эти должны на­ходиться друг от друга на расстоянии, не меньшем ее диаметра, ширина щелей ¾ близка расстоянию от Земли до Луны. «Пулемет» должен находиться на расстоянии сопоставимом с расстояния до Солнца, и стрелять «пу­лями», имеющими скорость полета намного больше второй космической скорости (>>11,5 км/с). Вот такая конструкция макромодели «пулемета» будет до некото­рой степени соответствовать структуре модели с двумя щелями для пролета электронов. Естественно, что вы­воды из стрельбы такого «пулемета» в перегородку с двумя отверстиями будут несколько отличаться от тех, к которым подводит студентов знаменитый курс лекций.

Поскольку, как совершенно правильно констатирует Р. Фейнман, нам еще не дано наблюдать за электроном, не нарушая траектории его движения, мы не сможем проследить его путь и, следовательно, точку, куда по­падет конкретный электрон. Но из этого вовсе не следу­ет, что траектория движения у него полностью отсутст­вует и мы не можем, задаваясь исходными параметрами электрона и зная количественные характеристики про­странств и отверстий, через которые он проходит, точно рассчитать его путь. Для теории в этом запретов нет. Есть технические ограничения для эмпирического под­тверждения теории и связано оно с недостижимостью необходимой точности в экспериментах. Эксперимента­тор не имеет (на сегодня) приборных возможностей оп­ределить, из какой щели вылетел электрон иди в какую он влетел уже потому, что для этого необходимо найти точку вхождения последнего в пространство атома с точностью на порядок меньше длины волны электрона.

Ивсе же, можно предложить эксперимент, позволяющий направлять полет электрона к строго определенной
щели и не влияющий на его движение по выходу из нее.
Это можно сделать следующим образом: Установить
электронную пушку 1внутри направляющего канала 2,
ведущего к двум щелям, и на некотором расстоянии от
нее по направлению к щелям разделить канал перего­родкой 3

на два канала, один из которых подходит к щели 4, а другой к щели 5 (рис. 67). В каждом из кана­лов может быть установ -

Рис. 67.

лен либо световой, либо электромагнит- ный индикатор 6, который и зафиксиру-ет прохождение элек- трона по каналу до того, как он дос­тигнет щели. И возмущение, полученное электроном при фиксации, не будет отражаться на его поведении после прохождения через щель. То есть будет отсутст­вовать искажение интерференционной картины.

Появ­ление же интерференции обусловлено наличием моду­лятора перед щелями (перегородка в канале) и за щелью
(утолщение в простенке) Таким образом, мож­но представить реаль­ный механизм «для оп­ределения того, через какое отверстие прохо­дит электрон» и тем самым еще раз поста­
вить под сомнение принцип неопределен­ности. Другое дело, что выполнить перегородку для прибора толщиной в пол-атома современная промыш­ленность не в состоянии. Но это технические трудно­сти, а не физические. И хотя еще нет физических спо­собов проследить, не влияя на электрон, по какой же траектории проходит его полет, можно однозначно
утверждать, что электрон летит по траектории, определяемой электромагнитной напряженностью поля атома. Это обстоятельство, по-видимому, будет до­казано только тогда, когда экспериментаторы нау­чатся работать с эфиром и его образованиями. Это время еще наступит.

5.5. Нецелочисленные радиусы орбит в атоме

Ранее было показано, что вурфные отношения золо­тых пропорций описывают взаимосвязи различных па­раметров одной системы и характер их зависимостей. Это свойство вурфных отношений может быть исполь­зовано для определения полноты различных числовых рядов. Рассмотрим, используя вурфы, например, полноту и целочисленность электронных орбит в атомах.

Как уже говорилось, одно из главных предположений Бора, обосновывающих структуру теории строения ато­ма, сформулировано следующим образом [ 92 ]:

«Основное» состояние любой системы, т.е. состояние, при котором излученная энергия максимальна, опреде­ляется из условия, что момент импульса каждого элек­трона относительно центра его орбиты был бы целым, кратным h/2p». (То есть целочисленным. - А. Ч.)

Согласно, этому предположению (постулату), внутри атома из бес­численного множества возможных орбит электрона реа­лизуются стационарные, орбитальный момент которых равен целому числу n, кратному h. Стационарные орби­ты (по Бору, ¾ единственно допустимые в атоме - А. Ч.) нумеруются целыми числами от 1 до бесконечности [ 97 ]: n = 1,2, 3,... ¥ (если это так, то какой же диаметр име­ет атом с галактику? Или больше? - А.Ч.), и постулируется, что данный ряд значений орбит полон, и существование других, промежуточных орбит с «нецелочисленными» номерами, невозможно. И потому n стало главным квантовым числом, открывшим систему квантования электронных орбит, а вместе с ними и квантовую меха­нику. Одновременно неявно постулировалась заданность и жесткость образующейся системы:

• все структурные взаимосвязи электронов однознач­но привязывались к п;

• постулировалась незаполненность пространства между ядром и боровской орбитой;

• боровский радиус практически становился и внеш­ней границей атома, и началом электронных орбит, создавая тем самым неопределенность статуса возни­кающей структуры, поскольку за границей атома начи­наются пространства других атомов.

Нарушение целочисленности орбитального момента, (существование между целочисленными промежуточных орбит), выявленное при совместном решение уравнений Бора (5.7) и Де Бройля (5.6) ставит под сомнение существование только целочисленных орбит, а вместе с ними и корректность и полноту всей квантовой механики. (Как следует из таблицы 10, промежутки между целочисленными орбитами заполнены еще неизвестными нецелочисленными орбитами электронов, они то и «образуют» промежуточные орбиты).

Для исследования полноты и целочисленности пара­метров электронных орбит а, v, Е, при n = 1,2, 3,..., 10, выпишем их количественную величину на первой боровской орбите из [ 22 ]:

а = 0,5292·10^-8 см - радиус боровской орбиты элек­трона, v = 2,188·10⁸ см/сек. - его скорость на этой орбите, Е = 2,181·10^-22 - энергия электрона на 1 -й боровской орбите.По известным уравнениям кван­товой механики, найдем количественную величину указанных параметров на n -х орбитах:

а_n = n²h²/me²; v_n = е²/nh; Е_n = me⁴/ 2 n²h². (5.12)

И занесем в табл. 11 по нисхо­дящей величине степени столбца п (нулевая строка таблицы). Добавляем в первую строку табл. 11 пара­метры массы электрона т = 9,110·10^-28 гр., заряда е = 4,803·10^-10, удельного заряда f = 5.273 ·10¹⁷, атомной гравитационной «постоянной» G = f² = 2,780 ·10³⁵, скоро­сти света с = 2,998·10¹⁰, и «постоянной» Ридберга R_¥ = l,097·10⁵ для бесконечной массы. Вносим в первую строку параметры частоты w и приведенной частоты u, рассчитав величины их столбцов пo уравнениям:

w_n = v/а_n; w_n = 2 pu_n

Таблица 11 заполнена. Даже по внешнему виду она достаточно непривлекательна и вызывает сомнение в своей истинности уже потому, что объединяет как бы в одну систему взаимосвязи, не подобные по своим свой­ствам, а потому и не связуемые качественно параметры: часть столбцов 3, 10-13, заполнена переменными вели­чинами, а столбцы 4-9 заполнены только в боровской строке так называемыми «фундаментальными постоянными». Каков механизм связи постоянных величин с пе­ременными, в квантовой механике не объясняется, а просто в неявной форме постулируется существование такого механизма.

Основная зависимость между переменными параметрами в табл. 11 образуется постулируемой целочисленностью орбит. Именно степень номера орбиты становится тем коэффициентом, который и обусловливает как взаимосвязь между «постоянными» и переменными параметрами, так и коэффициентную структуру изменения переменных параметров. Степенная величина коэффициента, образуемая номером орбиты для каждого параметра, вынесена в нулевую строку табл. 11 под индексами параметров.

Применив найденные в работе [9 ] уравнения (6)-(12):

ħ = а_nv_nm_n = е_n²/v_n = f_nе_nm_n/v_n = m_n²G_n/v_n = Е_n/w_n = Е_n/ 4 pс_nR_¥n. (5.13)

Убедимся, что соответствующая им постоянная Планка (ħ) может быть получена, как показано ранее, только с использованием величин параметров боровской строки табл. 11. По величинам параметров других строк (орбит) получение ħ без дополнительных постулатов не представляется возможным.

Фактически это означает, как уже отмечалось, что электрон, находящийся на первой орбите, движется и взаимодействует с ядром по одним законам, а с переходом на другую орбиту меняет систему взаимодействия и движется на них по другим законам, причем на каждой орбите по иному закону. В теории атома постулированием целочисленности орбит подбираются такие зависимости, которые обеспечивают «сшивание» переменных и «постоянных» величин только ограниченного количества параметров и, следовательно, уравнений. И только такие уравнения находят применение в современной квантовой механике. Совершенно корректный комплекс уравнений (5.13) не применим в ней уже потому, что никакими целочисленными величинами ¾ коэффициентами невозможно обеспечить в нем взаимосвязь «постоянных» и переменных параметров, поскольку в нем возможно использование только величин взаимосвязанных переменных параметров.

Имеются такие невостребованные уравнения и в клас­сической механике. Выпишем некоторые из них [ 46]:

m_nG_n = W_nG_n / v_n² = т_пv_n⁴R_n/W_n = v_n⁴R_n²/m_nG_n =

W_nR_n²v_n²/m_n²G_n =…= const, (5.14)

и отметим, что эти уравнения, как и постоянная Планка ħ, являются инвариантами и не находят применения в классической механике только потому, что масса тела т постулируется неизменной как во взаимодействиях, так и при изменении телом положения в гравитационном поле. А гравитационная «постоянная» G остается одной из фундаментальных постоянных классической механи­ки.

Таб лица 11, за исключением «фундаментальных по­стоянных», представляет собой матрицу размерных па­раметров, связанных степенной зависимостью по стро­кам и столбцам. И еще не найден математический аппарат, позволяющий определять полноту и совмести­мость образованного матрицей квантованного числового поля, а, следовательно, и корректность орбитальных за­висимостей боровской модели атома. Аппарат, приме­няемый в квантовой механике, такую задачу решить не в состоянии, поскольку в определении полноты и совмес­тимости элементов квантовой механики опора на внут­ренние структуры теории не дает определенного ответа. Требуется внешний, относительно теории кван­товой механики, математический аппарат, например, уже упомянутая система вурфных отношений [ 28]. Она обладает следующими достоинствами:

• базируется на степенных взаимосвязях русской матрицы;

• не является составной частью ни одной теоретиче­ской или математической системы, а потому ¾ внеш­няя для аппарата квантовой механики;

• охватывает матричную структуру как по строкам,
так и по столбцам;

• позволяет определять взаимосвязи многих параметров;

• проста и эффективна в расчетах.

Вурфные отношения ¾ абстракции и образуются либо взаимосвязанной системой коэффициентов, либо без­размерными модулями степенных параметров. Они от­ражают не количественные взаимосвязи между пара­метрами, а качествен-ные отношения значимостей в матрицах, составленных из количественных величин параметров. То есть с их помощью можно определить, обладает ли числовое поле рассматриваемой матрицы качествами природной системы.

Для проверки полноты параметров табл. 11 берутся, как уже говорилось, три последовательных значения па­раметры ¾ a, b, c и подставляются в вурфное отношение [ 28 ]:

W (а,b,с)= [(а + b)(b + с)] /b (а + b + с). (5.15)

Дата добавления: 2014-11-29