Влияние поперечных электрических полей на свойства сверхрешеток

Ранее уже указывалось, что электронные состояния в сверх­решетках образуют электронные зоны или подзоны, которые гораздо уже, чем соответствующие зоны в обычных кристаллах. Малая ширина зон и энергетических щелей является следствием того, что период сверхрешетки d обычно много больше постоянной а решетки кристалла.

Ниже будет показано, что при воздействии электрических полей электроны в таких узких зонах проявляют необычные свойства, демонстрируя существование некоторых физических эффектов (типа осцилляции Блоха), которые были, кстати, те­оретически предсказаны еще десятки лет назад. Кроме того, выяснилось, что под воздействием поля энергетические уров­ни ямы (шириной а) в сверхрешетке образуют так называемую штарковскую лестницу из «ступеней» высотой еFа, где F — при­ложенное электрическое поле.

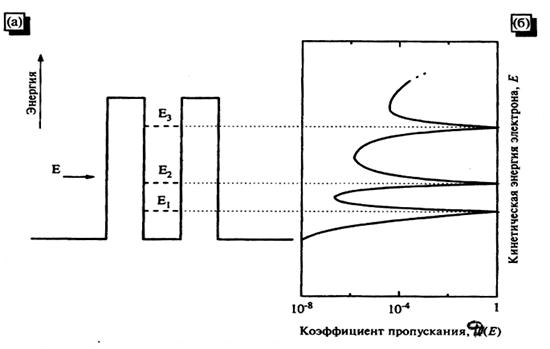
Рис. 6.7. (а) Схема преодоления электроном с энергией E двойного ре­зонансного барьера. Квантовая яма имеет три энергетических уровня (Е ₁, Е ₂и Е ₃);(б) зависимость коэффициента пропуска­ния от энергии падающего электрона.

Рассмотрим электронную зону в k -пространстве, по­казанную на рис. 6.8, которая похожа на первую подзону в сверхрешетке. Поле F прилагается в задан­ном направлении (мы обозначим его осью z, считая его на­правленным перпендикулярно к плоскости расположения квантовых ям), так что рассматриваемая задача сводится к одномерной. Движение электрона в такой зоне под влия­нием электрического поля описывается введенным в главе 2 уравнением (2.57)

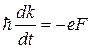, (6.4)

решением которого в случае постоянного поля является значе­ние волнового числа в виде

. (6.5)

В соответствии с решением (6.5) волновой вектор должен возрастать линейно по времени. Будем считать, что электрон первоначально покоился в точке О начала координатной оси, как показано на рис. 6.8, а направление электрического поля противоположно направлению вектора k. При этом электрон начинает двигаться из точки О по направлению к точке А,и это движение продолжается до тех пор, пока он не достигнет точки В, соответствующей границе зоны Бриллюэна (k = p/ d). В точке В его скорость уменьшается до нуля, в соответствии с нулевым углом наклона кривой, как следует из уравнения (2.52). После этого электрон переносится в точку С (по вектору обратной ре­шетки G),которой соответствует значение волнового вектора k = -p/ d,что просто означает результат брэгговского отраже­ния. Из точки С электрон в k -пространстве под воздействием поля смещается через точку В в точку О, за­вершая тем самым цикл движения. Скорость электрона при та­ком периодическом движении определяется уравнением

(6.6)

и также меняется периодически, если энергия зоны имеет вид, представленный на рис. 6.8. Иными словами, движение элек­трона является периодическим одновременно и в реальном, и в k -пространстве.

Период таких колебаний в k -пространстве Т_B определяется временем, необходимым для «прохождения» зоны Бриллюэна (= 2p/ d) и равен

. (6.7)

Рис. 6.8. Движение электрона внутри энергетической зоны в k -пространстве под воздействием приложенного электрического поля (процессы рассеяния не учитываются)

Следует отметить, что величины T_В и w _B зависят лишь от пе­риодичности сверхрешетки и напряженности приложенного поля, однако совершенно не зависят от ширины энергетической подзоны. Представляется очевидным, что для экспериментального наблю­дения блоховских осцилляции необходимо, чтобы период Т_В был меньше времени релаксации, связанного с процессами рассеяния. Ранее блоховские осцилляции экспериментально не могли быть зарегистрированы в объемных кристаллах в силу того, что харак­терные значения Т_B (~10^-11 с) значительно превышали соответству­ющие значения в сверхрешетках, поскольку величина d обычно на два порядка превосходит стандартные значения постоянной решет­ки в привычных полупроводниковых кристаллах. Эти ограничения приводили к тому, что электроны, расположенные близко к точ­ке О на диаграмме рис. 6.8, просто не могли получить достаточ­но энергии для достижения точки В на границе зоны Бриллюэна (k = p/ d),так как волновой вектор, определяемый уравнением (6.5), не мог возрастать до требуемого значения из-за процессов рассеяния, «отбрасывающих» электроны назад к точке О. С другой сто­роны, следует заметить, что в практических экспериментах значе­ние Т_B нельзя уменьшить просто за счет усиления напряженности прилагаемого поля F, поскольку при таком усилении возникает так называемое зеннеровское туннелирование (при котором электроны из наклонной подзоны, как показано на рис. 6.9, б, могут туннелировать через запрещенную зону в соседнюю подзону), в результате чего блоховские осцилляции вообще не возникают. Таким образом, для регистрации блоховских осцилляции необходимо иметь очень узкие подзоны и, наоборот, широкие мини-щели.

На рис. 6.9, а схематически приведена энергетическая струк­тура всего лишь двух подзон в сверхрешетке. При наложенном постоянном по величине электрическом поле F (направленном по оси z) зоны «наклоняются» под углом — еF,в результате чего выражение для потенциальной энергии приобретает вид

E (z) = E ₀ – eFz, (6.8)

где Е ₀ — энергия исходного состояния.

Рис. 6.9. (а) Подзоны в сверхрешетке; (б) наклон подзон в сверхрешетке под воздействием приложенного электрического поля

Вследствие показанного на рис. 6.9, б наклона зон электрон с полной энергией Е_Т может колебаться в пространстве между положениями с координатами z ₁ и z ₂.При возрастании значе­ния F наклон зон увеличивается, вследствие чего электрон про­странственно локализируется в меньшем объеме. Очевидно, что при очень высоких напряжениях приложенного поля электрон может быть локализирован в пределах одной квантовой ямы, для чего требуется, чтобы разность энергетических уровней D Е в двух соседних ямах превышала ширину подзон D, т. е. должно выполняться условие D Е = еFD > D. При этом квантовые ямы могут считаться несвязанными (рис. 6.10, а). Таким образом, при значениях электрического поля больше D /еd электроны ло­кализуются в квантовых ямах, чьи собственные энергетические состояния существенно различаются, в результате чего поня­тие подзон становится неприменимым. Вместо этого в систе­мах возникают новые структуры квантовых энергетических состояний, получившие название штарковских лестниц.

Рис. 6.10. (а) При наложении сильных электрических полей спектр подзон сверхрешетки разрушается, и на его месте возникает система, которую можно рассматривать в качестве множест­венных квантовых ям (MQW) с разностью энергий = eFd (б) вольт-амперная характеристика (I – V) сверхрешетки.

Такая штарковская локализация в сверхрешетках типа АlGaAs/GаАs была впервые зарегистрирована в эксперименте Мендесом, а затем нашла широкое применение в разнообразных электро­оптических приборах.

Подобно диодам с резонансным туннелированием, сверхре­шетки также имеют участки с отрицательным дифференциаль­ным сопротивлением (NDR) на вольт-амперных характеристи­ках, что может быть использовано в целом ряде электронных приборов. Такие участки возникают в наноструктурах при на­ложении настолько сильных электрических полей, что энергия соседних квантовых ям начинает различаться на величину, сравнимую с произведением eFd. В разделе 6.3.1 было показано, что резонансное туннелирование происходит при условии

Е ₂ – Е ₁ ,= еFd, (6.9)

где Е ₁и Е ₂означают энергии уровней при наложенном поле F, которые не должны обязательно совпадать с значениями при отсутствии поля (F= 0). Как показано на рис. 6.10, б, область проявления эффекта отрицательного дифференциального со­противления (NDR) располагается на вольт-амперной харак­теристике сверхрешетки сразу после резонансного пика, что позволяет использовать такие структуры, подобно диодам с ре­зонансным туннелированием, в качестве высокочастотных ос­цилляторов и усилителей.

Дата добавления: 2014-11-28