Формула Ландауэра — Бюттикера для квантового переноса в многозондовых структурах

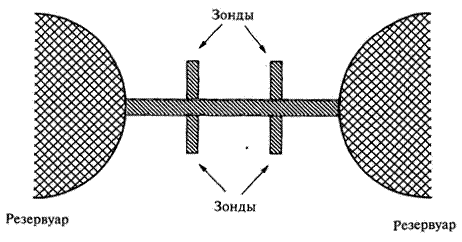
Полученное в предыдущем разделе выражение (6.15), описыва­ющее квантовый перенос в наноструктуре с двумя контактами, может быть обобщено на случай систем с большим числом кон­тактов. Рассмотрим, например, наноструктуру типа представлен­ной на рис. 6.13, похожую на те, которые часто используются в различных экспериментах, связанных с квантовым эффектом Холла, с двумя токовыми контактами, соединенные с соответствующими резервуарами и несколькими потенциаль­ными контактами. Резервуары в данном случае выступают в ка­честве бесконечных источников и стоков для электронов, причем их температура остается постоянной, даже когда они поставляют электроны в наноструктуру или поглощают их. Мы можем, как и выше, вычислить зависимость тока в каждом подводящем про­воде i, соединенном с резервуаром m_i, предполагая, что каждому из контактов соответствует лишь один канал. Аналогично мы можем построить матрицу рассеяния или прохождения из коэф­фициентов пропускания Т _ij,относящихся ко всем комбинациями индексов i и j. Поскольку электроны, попадающие в структуру от любого контакта, могут отражаться, мы должны ввести со­ответствующие коэффициенты отражения R _i. Кроме этого, для нахождения величины тока I _i (в контакте 1) мы должны учиты­вать и следующие факторы: 1) величину тока, инжектированного через контакт I из резервуара m_i, равную произведению (2 е / h)m_i;2) частичное отражение тока обратно в контакт, описываемое ко­эффициентом отражения R _i;3) все токи, поступающие в данный контакт i от других контактов. Сумма таких вкладов, с учетом знака, позволяет записать для тока I _i (в контакте i) выражение

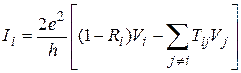, (6.16)

где через V_i обозначено напряжение, соответствующее m_i, т.е. m_i = е V_i. При этом следует отметить, что использованное выше обозначение V_i определяется относительно общего напряжения V ₀=m₀/ e, где m₀соответствует низшему уровню распределения Ферми в резервуарах, ниже которого все энергетические состояния заполнены и поэтому не могут никак участвовать в про­цессах переноса носителей заряда.

Очевидно, что при близких к T = 0К температурах величина m₀ должна совпадать с мини­мальным из значений уровней Ферми для всех m_i.

Рис. 6.13. Диаграмма типичной наноструктуры, используемой в экспе­риментальных измерениях, связанных с квантовым эффек­том Холла.

Приведенное уравнение получено для контактов с одним ка­налом. Многозондовое обобщение предполагает, что в каждом контакте i существует N_i каналов распространения, вследствие чего мы должны ввести обобщенные коэффициенты пропускания T _ij,ab, соответствующие вероятности носителя в контакте j и канале b перейти в контакт i канала a. Аналогично должны быть введены и обобщенные коэффициенты отражения R _i,ab соответствующие вероятности отражения носителя из канала b в канал a для одного и того же контакта i. Учитывая полные вклады в ток через контакт i, можно получить выражение

, (6.17)

где V _i- напряжение на резервуаре i, а Т _ijи R _i- приведенные коэф­фициенты пропускания и отражения, определяемые уравнениями

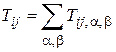и . (6.18)

Уравнение (6.17) называется формулой Ландауэра-Бюттикера квантового переноса в многозондовых системах.

1) n_i – является дискретным квантовым числом только в области энергий, соответствующих связанным состояниям, когда движение носителей заряда финитно.

Дата добавления: 2014-11-28